Statistics: Difference between revisions

From 太極
Jump to navigation Jump to search
Line 937: Line 937:


==== predict.coxph, prognostic index & risk score ====
==== predict.coxph, prognostic index & risk score ====
* https://www.rdocumentation.org/packages/survival/versions/2.41-2/topics/predict.coxph
* [https://www.rdocumentation.org/packages/survival/versions/2.41-2/topics/predict.coxph predict.coxph()] Compute fitted values and regression terms for a model fitted by coxph. The Cox model is a relative risk model; predictions of type "linear predictor", "risk", and "terms" are all relative to the sample from which they came. By default, the reference value for each of these is the mean covariate within strata. The primary underlying reason is statistical: a Cox model only predicts relative risks between pairs of subjects within the same strata, and hence the addition of a constant to any covariate, either overall or only within a particular stratum, has no effect on the fitted results. '''Returned value''': a vector or matrix of predictions, or a list containing the predictions (element "fit") and their standard errors (element "se.fit") if the se.fit option is TRUE.
<pre>
<pre>
predict(object, newdata,
predict(object, newdata,

Revision as of 13:31, 6 March 2018

Statisticians

Statistics for biologists

http://www.nature.com/collections/qghhqm

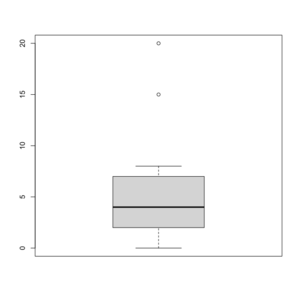
Box/Box and whisker plot in R

See http://msenux.redwoods.edu/math/R/boxplot.php for a numerical explanation how boxplot() in R works. 

> x=c(0,4,15, 1, 6, 3, 20, 5, 8, 1, 3)
> summary(x)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
      0       2       4       6       7      20 
> sort(x)
 [1]  0  1  1  3  3  4  5  6  8 15 20
> boxplot(x, col = 'grey')

Boxplot.svg

  • The lower and upper edges of box is determined by the first and 3rd quartiles (2 and 7 in the above example).
  • The thick dark horizon line is the median (4 in the example).
  • Outliers are defined by observations larger than 3rd quartile + 1.5 * IQR (7+1.5*5=14.5) and smaller than 1st quartile - 1.5 * IQR (2-1.5*5=-5.5). See the empty circles in the plot.
  • Upper whisker is defined by the largest data below 3rd quartile + 1.5 * IQR (8 in this example), and the lower whisker is defined by the smallest data greater than 1st quartile - 1.5 * IQR (0 in this example).

Note the wikipedia lists several possible definitions of a whisker. R uses the 2nd method (Tukey boxplot) to define whiskers.

stem and leaf plot

stem(). See http://www.r-tutor.com/elementary-statistics/quantitative-data/stem-and-leaf-plot R Tutorial].

BoxCox transformation

Finding transformation for normal distribution

the Holy Trinity (LRT, Wald, Score tests)

Don't invert that matrix

Linear Regression

Regression Models for Data Science in R by Brian Caffo

Comic https://xkcd.com/1725/

Different models (in R)

http://www.quantide.com/raccoon-ch-1-introduction-to-linear-models-with-r/

dummy.coef.lm() in R

Extracts coefficients in terms of the original levels of the coefficients rather than the coded variables.

Contrasts in linear regression

Multicollinearity

Multicollinearity in R

Confounders

Confidence interval vs prediction interval

Confidence intervals tell you about how well you have determined the mean E(Y). Prediction intervals tell you where you can expect to see the next data point sampled. That is, CI is computed using Var(E(Y|X)) and PI is computed using Var(E(Y|X) + e).

Non- and semi-parametric regression

Principal component analysis

R source code

> stats:::prcomp.default
function (x, retx = TRUE, center = TRUE, scale. = FALSE, tol = NULL, 
    ...) 
{
    x <- as.matrix(x)
    x <- scale(x, center = center, scale = scale.)
    cen <- attr(x, "scaled:center")
    sc <- attr(x, "scaled:scale")
    if (any(sc == 0)) 
        stop("cannot rescale a constant/zero column to unit variance")
    s <- svd(x, nu = 0)
    s$d <- s$d/sqrt(max(1, nrow(x) - 1))
    if (!is.null(tol)) {
        rank <- sum(s$d > (s$d[1L] * tol))
        if (rank < ncol(x)) {
            s$v <- s$v[, 1L:rank, drop = FALSE]
            s$d <- s$d[1L:rank]
        }
    }
    dimnames(s$v) <- list(colnames(x), paste0("PC", seq_len(ncol(s$v))))
    r <- list(sdev = s$d, rotation = s$v, center = if (is.null(cen)) FALSE else cen, 
        scale = if (is.null(sc)) FALSE else sc)
    if (retx) 
        r$x <- x %*% s$v
    class(r) <- "prcomp"
    r
}
<bytecode: 0x000000003296c7d8>
<environment: namespace:stats>

PCA and SVD

Using the SVD to perform PCA makes much better sense numerically than forming the covariance matrix to begin with, since the formation of XX⊤ can cause loss of precision.

http://math.stackexchange.com/questions/3869/what-is-the-intuitive-relationship-between-svd-and-pca

Related to Factor Analysis

In short,

  1. In Principal Components Analysis, the components are calculated as linear combinations of the original variables. In Factor Analysis, the original variables are defined as linear combinations of the factors.
  2. In Principal Components Analysis, the goal is to explain as much of the total variance in the variables as possible. The goal in Factor Analysis is to explain the covariances or correlations between the variables.
  3. Use Principal Components Analysis to reduce the data into a smaller number of components. Use Factor Analysis to understand what constructs underlie the data.

Calculated by Hand

http://strata.uga.edu/software/pdf/pcaTutorial.pdf

Do not scale your matrix

https://privefl.github.io/blog/(Linear-Algebra)-Do-not-scale-your-matrix/

Visualization

What does it do if we choose center=FALSE in prcomp()?

In USArrests data, use center=FALSE gives a better scatter plot of the first 2 PCA components. 

x1 = prcomp(USArrests) 
x2 = prcomp(USArrests, center=F)
plot(x1$x[,1], x1$x[,2])  # looks random
windows(); plot(x2$x[,1], x2$x[,2]) # looks good in some sense

Relation to Multidimensional scaling/MDS

With no missing data, classical MDS (Euclidean distance metric) is the same as PCA.

Comparisons are here.

Differences are asked/answered on stackexchange.com. The post also answered the question when these two are the same.

Matrix factorization methods

http://joelcadwell.blogspot.com/2015/08/matrix-factorization-comes-in-many.html Review of principal component analysis (PCA), K-means clustering, nonnegative matrix factorization (NMF) and archetypal analysis (AA).

Partial Least Squares (PLS)

Supervised vs. Unsupervised Learning: Exploring Brexit with PLS and PCA

Independent component analysis

ICA is another dimensionality reduction method.

ICA vs PCA

ICS vs FA

Correspondence analysis

https://francoishusson.wordpress.com/2017/07/18/multiple-correspondence-analysis-with-factominer/ and the book Exploratory Multivariate Analysis by Example Using R

t-SNE

t-Distributed Stochastic Neighbor Embedding (t-SNE) is a technique for dimensionality reduction that is particularly well suited for the visualization of high-dimensional datasets.

Visualize the random effects

http://www.quantumforest.com/2012/11/more-sense-of-random-effects/

ROC curve and Brier score

  • Binary case:
    • Y = true positive rate = sensitivity,
    • X = false positive rate = 1-specificity
  • Calibration
  • Introduction to the ROCR package.
  • http://freakonometrics.hypotheses.org/9066, http://freakonometrics.hypotheses.org/20002
  • Illustrated Guide to ROC and AUC
  • ROC Curves in Two Lines of R Code
  • Gini and AUC. Gini = 2*AUC-1.
  • 'Survival Model Predictive Accuracy and ROC Curves' by Heagerty & Zheng 2005
    • Sensitivity [math]\displaystyle{ P(\hat{p_i} \gt c | Y_i=1) }[/math], Specificity [math]\displaystyle{ P(\hat{p}_i \le c | Y_i=0 }[/math]), [math]\displaystyle{ Y_i }[/math] is binary outcomes, [math]\displaystyle{ \hat{p}_i }[/math] is a prediction, [math]\displaystyle{ c }[/math] is a criterion for classifying the prediction as positive ([math]\displaystyle{ \hat{p}_i \gt c }[/math]) or negative ([math]\displaystyle{ \hat{p}_i \le c }[/math]).
    • The AUC measures the probability that the marker value for a randomly selected case exceeds the marker value for a randomly selected control
    • ROC curves are useful for comparing the discriminatory capacity of different potential biomarkers.

Sensitivity/Specificity/Accuracy

Predict
1 0
True 1 TP FN Sens=TP/(TP+FN)
FNR=FN/(TP+FN)
0 FP TN Spec=TN/(FP+TN)
PPV=TP/(TP+FP)
FDR=FP/(TP+FP)		 NPV=TN/(FN+TN) N = TP + FP + FN + TN
  • Sensitivity = TP / (TP + FN)
  • Specificity = TN / (TN + FP)
  • Accuracy = (TP + TN) / N
  • False discovery rate FDR = FP / (TP + FP)
  • False negative rate FNR = FN / (TP + FN)
  • Positive predictive value (PPV) = TP / # positive calls = TP / (TP + FP) = 1 - FDR
  • Negative predictive value (NPV) = TN / # negative calls = TN / (FN + TN)
  • Prevalence = TP+FN/N.
  • Note that PPV & NPV can also be computed from sensitivity, specificity, and prevalence:
[math]\displaystyle{ \text{PPV} = \frac{\text{sensitivity} \times \text{prevalence}}{\text{sensitivity} \times \text{prevalence}+(1-\text{specificity}) \times (1-\text{prevalence})} }[/math]
[math]\displaystyle{ \text{NPV} = \frac{\text{specificity} \times (1-\text{prevalence})}{(1-\text{sensitivity}) \times \text{prevalence}+\text{specificity} \times (1-\text{prevalence})} }[/math]

Precision recall curve

Incidence, Prevalence

https://www.health.ny.gov/diseases/chronic/basicstat.htm

genefilter package and rowpAUCs function

  • rowpAUCs function in genefilter package. The aim is to find potential biomarkers whose expression level is able to distinguish between two groups.
# source("http://www.bioconductor.org/biocLite.R")
# biocLite("genefilter")
library(Biobase) # sample.ExpressionSet data
data(sample.ExpressionSet)

library(genefilter)
r2 = rowpAUCs(sample.ExpressionSet, "sex", p=0.1)
plot(r2[1]) # first gene, asking specificity = .9

r2 = rowpAUCs(sample.ExpressionSet, "sex", p=1.0)
plot(r2[1]) # it won't show pAUC

r2 = rowpAUCs(sample.ExpressionSet, "sex", p=.999)
plot(r2[1]) # pAUC is very close to AUC now

Maximum likelihood

Difference of partial likelihood, profile likelihood and marginal likelihood

Generalized Linear Model

Lectures from a course in Simon Fraser University Statistics.

Doing magic and analyzing seasonal time series with GAM (Generalized Additive Model) in R

Quasi Likelihood

Quasi-likelihood is like log-likelihood. The quasi-score function (first derivative of quasi-likelihood function) is the estimating equation.

Plot

https://strengejacke.wordpress.com/2015/02/05/sjplot-package-and-related-online-manuals-updated-rstats-ggplot/

Deviance

  • https://en.wikipedia.org/wiki/Deviance_(statistics)
  • Deviance = 2*(loglik_saturated - loglik_proposed)
  • It is a generalization of the idea of using the sum of squares of residuals in ordinary least squares to cases where model-fitting is achieved by maximum likelihood.
  • Interpreting Residual and Null Deviance in GLM R
    • Null Deviance = 2(LL(Saturated Model) - LL(Null Model)) on df = df_Sat - df_Null. The null deviance shows how well the response variable is predicted by a model that includes only the intercept (grand mean).
    • Residual Deviance = 2(LL(Saturated Model) - LL(Proposed Model)) df = df_Sat - df_Proposed
    • Null deviance > Residual deviance. Null deviance df = n-1. Residual deviance df = n-p.

Saturated model

Simulate data

Simulate data from a specified density

Signal to noise ratio

Var(f(X)) / Var(e) if Y = f(X) + e

Effect size

Multiple comparisons

Take an example, Suppose 550 out of 10,000 genes are significant at .05 level

  1. P-value < .05 ==> Expect .05*10,000=500 false positives
  2. False discovery rate < .05 ==> Expect .05*550 =27.5 false positives
  3. Family wise error rate < .05 ==> The probablity of at least 1 false positive <.05

False Discovery Rate

Suppose [math]\displaystyle{ p_1 \leq p_2 \leq ... \leq p_n }[/math]. Then [math]\displaystyle{ FDR_i = min(1, n* p_i/i) }[/math]. So if the number of tests ([math]\displaystyle{ n }[/math]) is large and/or the original p value ([math]\displaystyle{ p_i }[/math]) is large, then FDR can hit the value 1.

However, the simple formula above does not guarantee the monotonicity property from the FDR. So the calculation in R is more complicated. See How Does R Calculate the False Discovery Rate.

q-value

q-value is defined as the minimum FDR that can be attained when calling that feature significant (i.e., expected proportion of false positives incurred when calling that feature significant).

If gene X has a q-value of 0.013 it means that 1.3% of genes that show p-values at least as small as gene X are false positives.

SAM/Significance Analysis of Microarrays

The percentile option is used to define the number of falsely called genes based on 'B' permutations. If we use the 90-th percentile, the number of significant genes will be less than if we use the 50-th percentile/median.

In BRCA dataset, using the 90-th percentile will get 29 genes vs 183 genes if we use median.

Multivariate permutation test

In BRCA dataset, using 80% confidence gives 116 genes vs 237 genes if we use 50% confidence (assuming maximum proportion of false discoveries is 10%). The method is published on EL Korn, JF Troendle, LM McShane and R Simon, Controlling the number of false discoveries: Application to high dimensional genomic data, Journal of Statistical Planning and Inference, vol 124, 379-398 (2004).

String Permutations Algorithm

https://youtu.be/nYFd7VHKyWQ

Bayes

Bayes factor

Empirical Bayes method

Naive Bayes classifier

Understanding Naïve Bayes Classifier Using R

Offset in Poisson regression

https://stats.stackexchange.com/questions/11182/when-to-use-an-offset-in-a-poisson-regression

Overdispersion

https://en.wikipedia.org/wiki/Overdispersion

Var(Y) = phi * E(Y). If phi > 1, then it is overdispersion relative to Poisson. If phi <1, we have under-dispersion (rare).

Heterogeneity

The Poisson model fit is not good; residual deviance/df >> 1. The lack of fit maybe due to missing data, covariates or overdispersion.

Subjects within each covariate combination still differ greatly.

Consider Quasi-Poisson or negative binomial.

Test of overdispersion or underdispersion in Poisson models

https://stats.stackexchange.com/questions/66586/is-there-a-test-to-determine-whether-glm-overdispersion-is-significant

Negative Binomial

The mean of the Poisson distribution can itself be thought of as a random variable drawn from the gamma distribution thereby introducing an additional free parameter.

Survival data

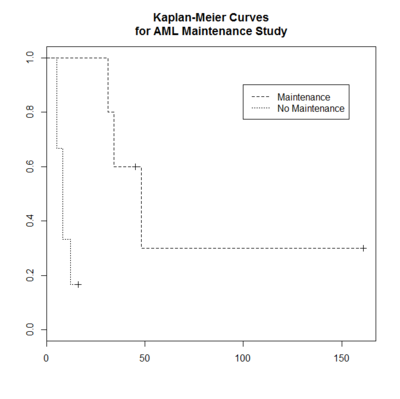
Kaplan & Meier and Nelson-Aalen: survfit.formula()

  • Curves are plotted in the same order as they are listed by print (which gives a 1 line summary of each). For example, -1 < 1 and 'Maintenance' < 'Nonmaintained'. That means, the labels list in the legend() command should have the same order as the curves.
  • Kaplan and Meier is used to give an estimator of the survival function S(t)
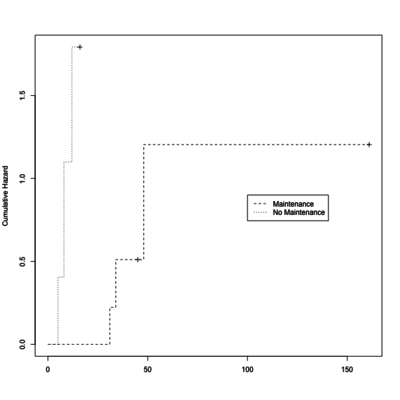
  • Nelson-Aalen estimator is for the cumulative hazard H(t). Note that [math]\displaystyle{ 0 \le H(t) \lt \infty }[/math] and [math]\displaystyle{ H(t) \rightarrow \infty }[/math] as t goes to infinity. So there is a constraint on the hazard function, see Wikipedia.

Note that S(t) is related to H(t) by [math]\displaystyle{ H(t) = -ln[S(t)]. }[/math] The two estimators are similar (see example 4.1A and 4.1B from Klein and Moeschberge).

The Nelson-Aalen estimator has two primary uses in analyzing data

  1. Selecting between parametric models for the time to event
  2. Crude estimates of the hazard rate h(t). This is related to the estimation of the survival function in Cox model. See 8.6 of Klein and Moeschberge.

The Kaplan–Meier estimator (the product limit estimator) is an estimator for estimating the survival function from lifetime data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment.

The "+" sign means censored observations and a long vertical line (not '+') means there is a dead observation at that time.

Usually the KM curve of treatment group is higher than that of the control group.

The Y-axis (the probability that a member from a given population will have a lifetime exceeding time) is often called

  • Cumulative probability
  • Cumulative survival
  • Percent survival
  • Probability without event
  • Proportion alive/surviving
  • Survival
  • Survival probability

KMcurve.png KMcurve cumhaz.png 

> library(survival)
> str(aml$x)
 Factor w/ 2 levels "Maintained","Nonmaintained": 1 1 1 1 1 1 1 1 1 1 ...
> plot(leukemia.surv <- survfit(Surv(time, status) ~ x, data = aml[7:17,] ) , 
      lty=2:3, mark.time = TRUE) # a (small) subset, mark.time is used to show censored obs
> aml[7:17,]
   time status             x
7    31      1    Maintained
8    34      1    Maintained
9    45      0    Maintained
10   48      1    Maintained
11  161      0    Maintained
12    5      1 Nonmaintained
13    5      1 Nonmaintained
14    8      1 Nonmaintained
15    8      1 Nonmaintained
16   12      1 Nonmaintained
17   16      0 Nonmaintained
> legend(100, .9, c("Maintenance", "No Maintenance"), lty = 2:3) # lty: 2=dashed, 3=dotted
> title("Kaplan-Meier Curves\nfor AML Maintenance Study") 

# Cumulative hazard plot
# Lambda(t) = -log(S(t)); 
# see https://en.wikipedia.org/wiki/Survival_analysis
# http://statweb.stanford.edu/~olshen/hrp262spring01/spring01Handouts/Phil_doc.pdf
plot(leukemia.surv <- survfit(Surv(time, status) ~ x, data = aml[7:17,] ) , 
      lty=2:3, mark.time = T, fun="cumhaz", ylab="Cumulative Hazard")
km <- survfit(Surv(time, status)~1, data=veteran)
survest <- stepfun(km$time, c(1, km$surv))
survest(0:100)

We can also use the plot() function to visual the plot. 

# Assume x and y have the same length.
plot(y ~ x, type = "s")

Survival curves with number at risk at bottom

R function survminer::ggsurvplot()

Paper examples

Survival curve with confidence interval

http://www.sthda.com/english/wiki/survminer-r-package-survival-data-analysis-and-visualization

Parametric models and survival function for censored data

Assume the CDF of survival time T is [math]\displaystyle{ F(\cdot) }[/math] and the CDF of the censoring time C is [math]\displaystyle{ G(\cdot) }[/math],

[math]\displaystyle{ \begin{align} P(T\gt t, \delta=1) &= \int_t^\infty (1-G(s))dF(s), \\ P(T\gt t, \delta=0) &= \int_t^\infty (1-F(s))dG(s) \end{align} }[/math]

Parametric models and likelihood function for uncensored data

plot.survfit()

  • Exponential. [math]\displaystyle{ T \sim Exp(\lambda) }[/math]. [math]\displaystyle{ H(t) = \lambda t. }[/math] and [math]\displaystyle{ ln(S(t)) = -H(t) = -\lambda t. }[/math]
  • Weibull. [math]\displaystyle{ T \sim W(\lambda,p). }[/math] [math]\displaystyle{ H(t) = \lambda^p t^p. }[/math] and [math]\displaystyle{ ln(-ln(S(t))) = ln(\lambda^p t^p)=const + p ln(t) }[/math].

http://www.math.ucsd.edu/~rxu/math284/slect4.pdf

See also accelerated life models where a set of covariates were used to model survival time.

Survival modeling

Accelerated life models - a direct extension of the classical linear model

http://data.princeton.edu/wws509/notes/c7.pdf and also Kalbfleish and Prentice (1980).

[math]\displaystyle{ log T_i = x_i' \beta + \epsilon_i }[/math] Therefore

  • [math]\displaystyle{ T_i = exp(x_i' \beta) T_{0i} }[/math]. So if there are two groups (x=1 and x=0), and [math]\displaystyle{ exp(\beta) = 2 }[/math], it means one group live twice as long as people in another group.
  • [math]\displaystyle{ S_1(t) = S_0(t/ exp(x' \beta)) }[/math]. This explains the meaning of accelerated failure-time. Depending on the sign of [math]\displaystyle{ \beta' Z }[/math], the time is either accelerated by a constant factor or degraded by a constant factor. If [math]\displaystyle{ exp(\beta)=2 }[/math], the probability that a member in group one (eg treatment) will be alive at age t is exactly the same as the probability that a member in group zero (eg control group) will be alive at age t/2.
  • The hazard function [math]\displaystyle{ \lambda_1(t) = \lambda_0(t/exp(x'\beta))/ exp(x'\beta) }[/math]. So if [math]\displaystyle{ exp(\beta)=2 }[/math], at any given age people in group one would be exposed to half the risk of people in group zero half their age.

In applications,

  • If the errors are normally distributed, then we obtain a log-normal model for the T. Estimation of this model for censored data by maximum likelihood is known in the econometric literature as a Tobit model.
  • If the errors have an extreme value distribution, then T has an exponential distribution. The hazard [math]\displaystyle{ \lambda }[/math] satisfies the log linear model [math]\displaystyle{ \log \lambda_i = x_i' \beta }[/math].

Proportional hazard models

Note PH models is a type of multiplicative hazard rate models [math]\displaystyle{ h(x|Z) = h_0(x)c(\beta' Z) }[/math] where [math]\displaystyle{ c(\beta' Z) = \exp(\beta ' Z) }[/math].

Assumption: Survival curves for two strata (determined by the particular choices of values for covariates) must have hazard functions that are proportional over time (i.e. constant relative hazard over time). Proportional hazards assumption meaning. The ratio of the hazard rates from two individuals with covariate value [math]\displaystyle{ Z }[/math] and [math]\displaystyle{ Z^* }[/math] is a constant function time.

[math]\displaystyle{ \begin{align} \frac{h(t|Z)}{h(t|Z^*)} = \frac{h_0(t)\exp(\beta 'Z)}{h_0(t)\exp(\beta ' Z^*)} = \exp(\beta' (Z-Z^*)) \mbox{ independent of time} \end{align} }[/math]

Test the assumption

  • cox.zph() can be used to test the proportional hazards assumption for a Cox regression model fit.
  • Log-log Kaplan-Meier curves and other methods.
  • https://stats.idre.ucla.edu/other/examples/asa2/testing-the-proportional-hazard-assumption-in-cox-models/. If the predictor satisfy the proportional hazard assumption then the graph of the survival function versus the survival time should results in a graph with parallel curves, similarly the graph of the log(-log(survival)) versus log of survival time graph should result in parallel lines if the predictor is proportional. This method does not work well for continuous predictor or categorical predictors that have many levels because the graph becomes to “cluttered”.

Cox Regression

Weibull and Exponential model to Cox model

In summary:

  • Weibull distribution (Klein) [math]\displaystyle{ h(t) = p \lambda (\lambda t)^{p-1} }[/math] and [math]\displaystyle{ S(t) = exp(-\lambda t^p) }[/math]. If p >1, then the risk increases over time. If p<1, then the risk decreases over time.
    • Note that Weibull distribution has a different parametrization. See http://data.princeton.edu/pop509/ParametricSurvival.pdf#page=2. [math]\displaystyle{ h(t) = \lambda^p p t^{p-1} }[/math] and [math]\displaystyle{ S(t) = exp(-(\lambda t)^p) }[/math]. R and wikipedia also follows this parametrization except that [math]\displaystyle{ h(t) = p t^{p-1}/\lambda^p }[/math] and [math]\displaystyle{ S(t) = exp(-(t/\lambda)^p) }[/math].
  • Exponential distribution [math]\displaystyle{ h(t) }[/math] = constant (independent of t). This is a special case of Weibull distribution (p=1).
  • Weibull (and also exponential) distribution is the only case which belongs to both the proportional hazards and the accelerated life families.
[math]\displaystyle{ \begin{align} \frac{h(x|Z_1)}{h(x|Z_2)} = \frac{h_0(x\exp(-\gamma' Z_1)) \exp(-\gamma ' Z_1)}{h_0(x\exp(-\gamma' Z_2)) \exp(-\gamma ' Z_2)} = \frac{(a/b)\left(\frac{x \exp(-\gamma ' Z_1)}{b}\right)^{a-1}\exp(-\gamma ' Z_1)}{(a/b)\left(\frac{x \exp(-\gamma ' Z_2)}{b}\right)^{a-1}\exp(-\gamma ' Z_2)} \quad \mbox{which is independent of time x} \end{align} }[/math]
f(t)=h(t)*S(t) h(t) S(t) Mean
Exponential (Klein p37) [math]\displaystyle{ \lambda \exp(-\lambda t) }[/math] [math]\displaystyle{ \lambda }[/math] [math]\displaystyle{ \exp(-\lambda t) }[/math] [math]\displaystyle{ 1/\lambda }[/math]
Weibull (Klein, wikipedia) [math]\displaystyle{ p\lambda t^{p-1}\exp(-\lambda t^p) }[/math] [math]\displaystyle{ p\lambda t^{p-1} }[/math] [math]\displaystyle{ exp(-\lambda t^p) }[/math] [math]\displaystyle{ \frac{\Gamma(1+1/p)}{\lambda^{1/p}} }[/math]
Exponential (R) [math]\displaystyle{ \lambda \exp(-\lambda t) }[/math], [math]\displaystyle{ \lambda }[/math] is rate [math]\displaystyle{ \lambda }[/math] [math]\displaystyle{ \exp(-\lambda t) }[/math] [math]\displaystyle{ 1/\lambda }[/math]
Weibull (R, wikipedia) [math]\displaystyle{ \frac{a}{b}\left(\frac{x}{b}\right)^{a-1} \exp(-(\frac{x}{b})^a) }[/math],
[math]\displaystyle{ a }[/math] is shape, and [math]\displaystyle{ b }[/math] is scale		 [math]\displaystyle{ \frac{a}{b}\left(\frac{x}{b}\right)^{a-1} }[/math] [math]\displaystyle{ \exp(-(\frac{x}{b})^a) }[/math] [math]\displaystyle{ b\Gamma(1+1/a) }[/math]
  • Accelerated failure-time model. Let [math]\displaystyle{ Y=\log(T)=\mu + \gamma'Z + \sigma W }[/math]. Then the survival function of [math]\displaystyle{ T }[/math] at the covariate Z,
[math]\displaystyle{ \begin{align} S_T(t|Z) &= P(T \gt t |Z) \\ &= P(Y \gt \ln t|Z) \\ &= P(\mu + \sigma W \gt \ln t-\gamma' Z | Z) \\ &= P(e^{\mu + \sigma W} \gt t\exp(-\gamma'Z) | Z) \\ &= S_0(t \exp(-\gamma'Z)). \end{align} }[/math]

where [math]\displaystyle{ S_0(t) }[/math] denote the survival function T when Z=0. Since [math]\displaystyle{ h(t) = -\partial \ln (S(t)) }[/math], the hazard function of T with a covariate value Z is related to a baseline hazar rate [math]\displaystyle{ h_0 }[/math] by (p56 Klein)

[math]\displaystyle{ \begin{align} h(t|Z) = h_0(t\exp(-\gamma' Z)) \exp(-\gamma ' Z) \end{align} }[/math]
> mean(rexp(1000)^(1/2))
[1] 0.8902948
> mean(rweibull(1000, 2, 1))
[1] 0.8856265

> mean((rweibull(1000, 2, scale=4)/4)^2)
[1] 1.008923

Simulate survival data

Note that status = 1 means an event (e.g. death) happened; Ti <= Ci. That is, the status variable used in R/Splus means the death indicator. 

x <- (1:30)/2 - 3 # create the covariates, 30 of them
myrates <- exp(3*x+1) # the risk exp(beta*x), parameters for exp r.v.
set.seed(1234)
y <- rexp(30, rate = myrates) # generates the r.v.
cen <- rexp(30, rate = 0.5 )  #  E(cen)=1/rate
ycen <- pmin(y, cen)
di <- as.numeric(y <= cen)
survreg(Surv(ycen, di)~x, dist="weibull")$coef[2]  # -3.004877
coxph(Surv(ycen, di)~x)$coef  # 0.4852654 

# no censor
survreg(Surv(y,rep(1,30))~x,dist="weibull")$coef[2]  # -3.031261
survreg(Surv(y,rep(1,30))~x,dist="exponential")$coef[2]  # -3.032509
coxph(Surv(y,rep(1,30))~x)$coef  # 0.4407214 

# See the pdf note for the rest of code
[math]\displaystyle{ \begin{align} \lambda = exp(-intercept) \end{align} }[/math]
> futime <- rexp(1000, 5)
> survreg(Surv(futime,rep(1,1000))~1,dist="exponential")$coef
(Intercept) 
  -1.618263 
> exp(1.618263)
[1] 5.044321
[math]\displaystyle{ \begin{align} \gamma &= 1/scale \\ \alpha &= exp(-(Intercept)*\gamma) \end{align} }[/math]
> survreg(Surv(futime,rep(1,1000))~1,dist="weibull")
Call:
survreg(formula = Surv(futime, rep(1, 1000)) ~ 1, dist = "weibull")

Coefficients:
(Intercept) 
  -1.639469 

Scale= 1.048049 

Loglik(model)= 620.1   Loglik(intercept only)= 620.1
n= 1000
  • rsurv() function from the ipred package
  • survsim package. See this post.
  • Use Weibull distribution to model survival data. We assume the shape is constant across subjects. We then allow the scale to vary across subjects. For subject [math]\displaystyle{ i }[/math] with covariate [math]\displaystyle{ X_i }[/math], [math]\displaystyle{ \log(scale_i) }[/math] = [math]\displaystyle{ \beta ' X_i }[/math]. Note that if we want to make the [math]\displaystyle{ \beta }[/math] sign to be consistent with the Cox model, we want to use [math]\displaystyle{ \log(scale_i) }[/math] = [math]\displaystyle{ -\beta ' X_i }[/math] instead.
  • http://sas-and-r.blogspot.com/2010/03/example-730-simulate-censored-survival.html. Assuming shape=1 in the Weibull distribution, then the hazard function can be expressed as a proportional hazard model

[math]\displaystyle{ h(t|x) = 1/scale = \frac{1}{\lambda/e^{\beta 'x}} = \frac{e^{\beta ' x}}{\lambda} = h_0(t) \exp(\beta' x) }[/math] 

n = 10000
beta1 = 2; beta2 = -1
lambdaT = .002 # baseline hazard
lambdaC = .004  # hazard of censoring
set.seed(1234)
x1 = rnorm(n,0)
x2 = rnorm(n,0)
# true event time
T = rweibull(n, shape=1, scale=lambdaT*exp(-beta1*x1-beta2*x2)) 
# No censoring
event2 <- rep(1, length(T))
coxph(Surv(T, event2)~ x1 + x2)
#       coef exp(coef) se(coef)     z      p
# x1  1.9982    7.3761   0.0188 106.1 <2e-16
# x2 -1.0020    0.3671   0.0127 -79.1 <2e-16
#
# Likelihood ratio test=15556  on 2 df, p=0
# n= 10000, number of events= 10000 

# Censoring
C = rweibull(n, shape=1, scale=lambdaC)   #censoring time
time = pmin(T,C)  #observed time is min of censored and true
event = time==T   # set to 1 if event is observed
coxph(Surv(time, event)~ x1 + x2)
#       coef exp(coef) se(coef)     z      p
# x1  2.0104    7.4662   0.0225  89.3 <2e-16
# x2 -0.9921    0.3708   0.0155 -63.9 <2e-16
#
# Likelihood ratio test=11321  on 2 df, p=0
# n= 10000, number of events= 6002

Predefined censoring rates

Simulating survival data with predefined censoring rates for proportional hazards models

glmnet + Cox models

Error in glmnet: x should be a matrix with 2 or more columns

https://stackoverflow.com/questions/29231123/why-cant-pass-only-1-coulmn-to-glmnet-when-it-is-possible-in-glm-function-in-r

Error in coxnet: (list) object cannot be coerced to type 'double'

Fix: do not use data.frame in X. Use cbind() instead.

Predicted survival probabilities

## S3 method for class 'glmnet'
predictProb(object, response, x, times, complexity, ...)
expSurv(res, traindata, method, ci.level = .95, boot = FALSE, nboot, smooth = TRUE,
  pct.group = 4, horizon, trace = TRUE, ncores = 1)

Cross validation

  • Cross validation in survival analysis by Verweij & van Houwelingen, Stat in medicine 1993.
  • Using cross-validation to evaluate predictive accuracy of survival risk classifiers based on high-dimensional data. Simon et al, Brief Bioinform. 2011

Survival rate

Books

HER2-positive breast cancer

Cox Regression

Let Yi denote the observed time (either censoring time or event time) for subject i, and let Ci be the indicator that the time corresponds to an event (i.e. if Ci = 1 the event occurred and if Ci = 0 the time is a censoring time). The hazard function for the Cox proportional hazard model has the form

[math]\displaystyle{ \lambda(t|X) = \lambda_0(t)\exp(\beta_1X_1 + \cdots + \beta_pX_p) = \lambda_0(t)\exp(X \beta^\prime). }[/math]

This expression gives the hazard at time t for an individual with covariate vector (explanatory variables) X. Based on this hazard function, a partial likelihood (defined on hazard function) can be constructed from the datasets as

[math]\displaystyle{ L(\beta) = \prod_{i:C_i=1}\frac{\theta_i}{\sum_{j:Y_j\ge Y_i}\theta_j}, }[/math]

where θj = exp(Xj β′) and X1, ..., Xn are the covariate vectors for the n independently sampled individuals in the dataset (treated here as column vectors). This pdf or this note give a toy example

The corresponding log partial likelihood is

[math]\displaystyle{ \ell(\beta) = \sum_{i:C_i=1} \left(X_i \beta^\prime - \log \sum_{j:Y_j\ge Y_i}\theta_j\right). }[/math]

This function can be maximized over β to produce maximum partial likelihood estimates of the model parameters.

The partial score function is [math]\displaystyle{ \ell^\prime(\beta) = \sum_{i:C_i=1} \left(X_i - \frac{\sum_{j:Y_j\ge Y_i}\theta_jX_j}{\sum_{j:Y_j\ge Y_i}\theta_j}\right), }[/math]

and the Hessian matrix of the partial log likelihood is

[math]\displaystyle{ \ell^{\prime\prime}(\beta) = -\sum_{i:C_i=1} \left(\frac{\sum_{j:Y_j\ge Y_i}\theta_jX_jX_j^\prime}{\sum_{j:Y_j\ge Y_i}\theta_j} - \frac{\sum_{j:Y_j\ge Y_i}\theta_jX_j\times \sum_{j:Y_j\ge Y_i}\theta_jX_j^\prime}{[\sum_{j:Y_j\ge Y_i}\theta_j]^2}\right). }[/math]

Using this score function and Hessian matrix, the partial likelihood can be maximized using the Newton-Raphson algorithm. The inverse of the Hessian matrix, evaluated at the estimate of β, can be used as an approximate variance-covariance matrix for the estimate, and used to produce approximate standard errors for the regression coefficients.

If X is age, then the coefficient is likely >0. If X is some treatment, then the coefficient is likely <0.

Compare the partial likelihood to the full likelihood

http://math.ucsd.edu/~rxu/math284/slect5.pdf#page=10

Partial likelihood when there are ties

http://math.ucsd.edu/~rxu/math284/slect5.pdf#page=29

Hazard (function) and survival function

A hazard is the rate at which events happen, so that the probability of an event happening in a short time interval is the length of time multiplied by the hazard.

[math]\displaystyle{ h(t) = \lim_{\Delta t \to 0} \frac{P(t \leq T \lt t+\Delta t|T \geq t)}{\Delta t} = \frac{f(t)}{S(t)} = -\partial{ln[S(t)]} }[/math]

Therefore

[math]\displaystyle{ H(x) = \int_0^x h(u) d(u) = -ln[S(x)]. }[/math]

or

[math]\displaystyle{ S(x) = e^{-H(x)} }[/math]

Hazards (or probability of hazards) may vary with time, while the assumption in proportional hazard models for survival is that the hazard is a constant proportion.

Examples:

  • If h(t)=c, S(t) is exponential. f(t) = c exp(-ct). The mean is 1/c.
  • If [math]\displaystyle{ \log h(t) = c + \rho t }[/math], S(t) is Gompertz distribution.
  • If [math]\displaystyle{ \log h(t)=c + \rho \log (t) }[/math], S(t) is Weibull distribution.
  • For Cox regression, the survival function can be shown to be [math]\displaystyle{ S(t|X) = S_0(t) ^ {\exp(X\beta)} }[/math].
[math]\displaystyle{ \begin{align} S(t|X) &= e^{-H(t)} = e^{-\int_0^t h(u|X)du} \\ &= e^{-\int_0^t h_0(u) exp(X\beta) du} \\ &= e^{-\int_0^t h_0(u) du \cdot exp(X \beta)} \\ &= S_0(t)^{exp(X \beta)} \end{align} }[/math]

Alternatively,

[math]\displaystyle{ \begin{align} S(t|X) &= e^{-H(t)} = e^{-\int_0^t h(u|X)du} \\ &= e^{-\int_0^t h_0(u) exp(X\beta) du} \\ &= e^{-H_0(t) \cdot exp(X \beta)} \end{align} }[/math]

where the cumulative baseline hazard at time t, [math]\displaystyle{ H_0(t) }[/math], is commonly estimated through the non-parametric Breslow estimator.

Predicted survival probability in Cox model: survfit.coxph() & summary.survfit(times)

For theory, see section 8.6 Estimation of the survival function in Klein & Moeschberger.

For R, see Extract survival probabilities in Survfit by groups

The plot function below will draw 4 curves: [math]\displaystyle{ S_0(t)^{\exp(\hat{\beta}_{age}*60)} }[/math], [math]\displaystyle{ S_0(t)^{\exp(\hat{\beta}_{age}*60+\hat{\beta}_{stageII})} }[/math], [math]\displaystyle{ S_0(t)^{\exp(\hat{\beta}_{age}*60+\hat{\beta}_{stageIII})} }[/math], [math]\displaystyle{ S_0(t)^{\exp(\hat{\beta}_{age}*60+\hat{\beta}_{stageIV})} }[/math]. 

library(KMsurv) # Data package for Klein & Moeschberge
data(larynx)
larynx$stage <- factor(larynx$stage)
coxobj <- coxph(Surv(time, delta) ~ age + stage, data = larynx)

# Figure 8.3 from Section 8.6
plot(survfit(coxobj, newdata = data.frame(age=rep(60, 4), stage=factor(1:4))), lty = 1:4)

# Estimated probability for a 60-year old for different stage patients
out <- summary(survfit(coxobj, data.frame(age = rep(60, 4), stage=factor(1:4))), times = 5)
out$surv
#  time n.risk n.event survival1 survival2 survival3 survival4
#    5     34      40     0.702     0.665      0.51     0.142
sum(larynx$time >=5) # n.risk
# [1] 34
sum(larynx$delta[larynx$time <=5]) # n.event
# [1] 40
sum(larynx$time >5) # Wrong
# [1] 31
sum(larynx$delta[larynx$time <5]) # Wrong
# [1] 39

# 95% confidence interval
out$lower
# 0.8629482 0.9102532 0.7352413 0.548579
out$upper
# 0.5707952 0.4864903 0.3539527 0.03691768

We need to pay attention when the number of covariates is large (and we don't want to specify each covariates in the formula). The key is to create a data frame and use dot (.) in the formula. This is to fix a warning message: 'newdata' had XXX rows but variables found have YYY rows from running survfit(, newdata).

Another way is to use as.formula() if we don't want to create a new object. 

xsub <- data.frame(xtrain)
colnames(xsub) <- paste0("x", 1:ncol(xsub))

coxobj <- coxph(Surv(ytrain[, "time"], ytrain[, "status"]) ~ ., data = xsub)

newdata <- data.frame(xtest)
colnames(newdata) <- paste0("x", 1:ncol(newdata))

survprob <- summary(survfit(coxobj, newdata=newdata), 
                    times = 5)$surv[1, ]  
# since there is only 1 time point, we select the first row in surv (surv is a matrix with one row).

Expectation of life & expected future lifetime

  • The average lifetime is the same as the area under the survival curve.
[math]\displaystyle{ \begin{align} \mu &= \int_0^\infty t f(t) dt \\ &= \int_0^\infty S(t) dt \end{align} }[/math]

by integrating by parts making use of the fact that -f(t) is the derivative of S(t), which has limits S(0)=1 and [math]\displaystyle{ S(\infty)=0 }[/math]. The average lifetime may not be bounded if you have censored data, there's censored observations that last beyond your last recorded death.

[math]\displaystyle{ \frac{1}{S(t_0)} \int_0^{\infty} t\,f(t_0+t)\,dt = \frac{1}{S(t_0)} \int_{t_0}^{\infty} S(t)\,dt, }[/math]

Hazard Ratio

A hazard ratio is often reported as a “reduction in risk of death or progression” – This risk reduction is calculated as 1 minus the Hazard Ratio (exp^beta), e.g., HR of 0.84 is equal to a 16% reduction in risk. See www.time4epi.com and stackexchange.com.

Another example (John Fox) is assuming Y ~ age + prio + others.

  • If exp(beta_age) = 0.944. It means an additional year of age reduces the hazard by a factor of .944 on average, or (1-.944)*100 = 5.6 percent.
  • If exp(beta_prio) = 1.096, it means each prior conviction increases the hazard by a factor of 1.096, or 9.6 percent.

Hazard ratio is not the same as the relative risk ratio. See medicine.ox.ac.uk.

Interpreting risks and ratios in therapy trials from australianprescriber.com is useful too.

For two groups that differ only in treatment condition, the ratio of the hazard functions is given by [math]\displaystyle{ e^\beta }[/math], where [math]\displaystyle{ \beta }[/math] is the estimate of treatment effect derived from the regression model. See here.

Compute ratio ratios from coxph() in R (Hint: exp(beta)).

Prognostic index is defined on http://www.math.ucsd.edu/~rxu/math284/slect6.pdf#page=2.

Basics of the Cox proportional hazards model. Good prognostic factor (b<0 or HR<1) and bad prognostic factor (b>0 or HR>1).

Variable selection: variables were retained in the prediction models if they had a hazard ratio of <0.85 or >1.15 (for binary variables) and were statistically significant at the 0.01 level. see Development and validation of risk prediction equations to estimate survival in patients with colorectal cancer: cohort study.

Hazard Ratio and death probability

https://en.wikipedia.org/wiki/Hazard_ratio#The_hazard_ratio_and_survival

Suppose S0(t)=.2 (20% survived at time t) and the hazard ratio (hr) is 2 (a group has twice the chance of dying than a comparison group), then (Cox model is assumed)

  1. S1(t)=S0(t)hr = .22 = .04 (4% survived at t)
  2. The corresponding death probabilities are 0.8 and 0.96.
  3. If a subject is exposed to twice the risk of a reference subject at every age, then the probability that the subject will be alive at any given age is the square of the probability that the reference subject (covariates = 0) would be alive at the same age. See p10 of this lecture notes.
  4. exp(x*beta) is the relative risk associated with covariate value x.

Hazard Ratio Forest Plot

The forest plot quickly summarizes the hazard ratio data across multiple variables –If the line crosses the 1.0 value, the hazard ratio is not significant and there is no clear advantage for either arm.

Estimate baseline hazard [math]\displaystyle{ h_0(t) }[/math] and cumulative baseline hazard [math]\displaystyle{ H_0(t) }[/math]

Google: how to estimate baseline hazard rate

Prognostic index/risk scores

linear.predictors component in coxph object

The $linear.predictors component is not [math]\displaystyle{ \beta' x }[/math]. It is [math]\displaystyle{ \beta' (x-\mu_x) }[/math]. See this post.

predict.coxph, prognostic index & risk score

  • predict.coxph() Compute fitted values and regression terms for a model fitted by coxph. The Cox model is a relative risk model; predictions of type "linear predictor", "risk", and "terms" are all relative to the sample from which they came. By default, the reference value for each of these is the mean covariate within strata. The primary underlying reason is statistical: a Cox model only predicts relative risks between pairs of subjects within the same strata, and hence the addition of a constant to any covariate, either overall or only within a particular stratum, has no effect on the fitted results. Returned value: a vector or matrix of predictions, or a list containing the predictions (element "fit") and their standard errors (element "se.fit") if the se.fit option is TRUE.
predict(object, newdata,
    type=c("lp", "risk", "expected", "terms", "survival"),
    se.fit=FALSE, na.action=na.pass, terms=names(object$assign), collapse,
    reference=c("strata", "sample"),  ...)

library(coxph)
fit <- coxph(Surv(time, status) ~ age , lung)
fit
#  Call:
#  coxph(formula = Surv(time, status) ~ age, data = lung)
#       coef exp(coef) se(coef)    z     p
# age 0.0187      1.02   0.0092 2.03 0.042
#
# Likelihood ratio test=4.24  on 1 df, p=0.0395  n= 228, number of events= 165 
fit$means
#      age 
# 62.44737 

# type = "lr" (Linear predictor)
as.numeric(predict(fit,type="lp"))[1:10]   
# [1]  0.21626733  0.10394626 -0.12069589 -0.10197571 -0.04581518  0.21626733
# [7]  0.10394626  0.16010680 -0.17685643 -0.02709500
0.0187 * (lung$age[1:10] - fit$means)
# [1]  0.21603421  0.10383421 -0.12056579 -0.10186579 -0.04576579  0.21603421
# [7]  0.10383421  0.15993421 -0.17666579 -0.02706579
fit$linear.predictors[1:10]
# [1]  0.21626733  0.10394626 -0.12069589 -0.10197571 -0.04581518
# [6]  0.21626733  0.10394626  0.16010680 -0.17685643 -0.02709500

# type = "risk" (Risk score)
> as.numeric(predict(fit,type="risk"))[1:10]
 [1] 1.2414342 1.1095408 0.8863035 0.9030515 0.9552185 1.2414342 1.1095408
 [8] 1.1736362 0.8379001 0.9732688
> exp((lung$age-mean(lung$age)) * 0.0187)[1:10]
 [1] 1.2411448 1.1094165 0.8864188 0.9031508 0.9552657 1.2411448
 [7] 1.1094165 1.1734337 0.8380598 0.9732972
> exp(fit$linear.predictors)[1:10]
 [1] 1.2414342 1.1095408 0.8863035 0.9030515 0.9552185 1.2414342
 [7] 1.1095408 1.1736362 0.8379001 0.9732688

Survival risk prediction

Assessing the performance of prediction models

Hazard ratio

hazard.ratio() 

hazard.ratio(x, surv.time, surv.event, weights, strat, alpha = 0.05, 
             method.test = c("logrank", "likelihood.ratio", "wald"), na.rm = FALSE, ...)

D index

D.index() 

D.index(x, surv.time, surv.event, weights, strat, alpha = 0.05, 
        method.test = c("logrank", "likelihood.ratio", "wald"), na.rm = FALSE, ...)

Concordance index (C-index)

See also 5 Ways to Estimate Concordance Index for Cox Models in R, Why Results Aren't Identical?

Integrated brier score

Assessment and comparison of prognostic classification schemes for survival data Graf et al Stat. Med. 1999 2529-45

  • Because the point predictions of event-free times will almost inevitably given inaccurate and unsatisfactory result, the mean square error of prediction [math]\displaystyle{ \frac{1}{n}\sum_1^n (T_i - \hat{T}(X_i))^2 }[/math] method will not be considered.
  • Another approach is to predict the survival or event status [math]\displaystyle{ Y=I(T \gt \tau) }[/math] at a fixed time point [math]\displaystyle{ \tau }[/math] for a patient with X=x. This leads to the expected Brier score [math]\displaystyle{ E[(Y - \hat{S}(\tau|X))^2] }[/math] where [math]\displaystyle{ \hat{S}(\tau|X) }[/math] is the estimated event-free probabilities (survival probability) at time [math]\displaystyle{ \tau }[/math] for subject with predictor variable [math]\displaystyle{ X }[/math].
  • The time-dependent Brier score (without censoring)
[math]\displaystyle{ \begin{align} \mbox{Brier}(\tau) &= \frac{1}{n}\sum_1^n (I(T_i\gt \tau) - \hat{S}(\tau|X_i))^2 \end{align} }[/math]
  • The time-dependent Brier score (with censoring, C is the censoring variable)
[math]\displaystyle{ \begin{align} \mbox{Brier}(\tau) = \frac{1}{n}\sum_i^n\bigg[\frac{(\hat{S}_C(t_i))^2I(t_i \leq \tau, \delta_i=1)}{\hat{S}_C(t_i)} + \frac{(1 - \hat{S}_C(t_i))^2 I(t_i \gt \tau)}{\hat{S}_C(\tau)}\bigg] \end{align} }[/math]

where [math]\displaystyle{ \hat{S}_C(t_i) = P(C \gt t_i) }[/math], the Kaplan-Meier estimate of the censoring distribution with [math]\displaystyle{ t_i }[/math] the survival time of patient i. The integration of the Brier score can be done by over time [math]\displaystyle{ t \in [0, \tau] }[/math] with respect to some weight function W(t) for which a natual choice is [math]\displaystyle{ (1 - \hat{S}(t))/(1-\hat{S}(\tau)) }[/math]. The lower the iBrier score, the larger the prediction accuracy is.

  • Useful benchmark values for the Brier score are 33%, which corresponds to predicting the risk by a random number drawn from U[0, 1], and 25% which corresponds to predicting 50% risk for everyone. See Evaluating Random Forests for Survival Analysis using Prediction Error Curves by Mogensen et al J. Stat Software 2012 (pec package). The paper has a good summary of different R package implementing Brier scores.

R function

Papers on high dimensional covariates

  • Assessment of survival prediction models based on microarray data, Bioinformatics , 2007, vol. 23 (pg. 1768-74)
  • Allowing for mandatory covariates in boosting estimation of sparse high-dimensional survival models, BMC Bioinformatics , 2008, vol. 9 pg. 14

C-statistics

  • On the C-statistics for Evaluating Overall Adequacy of Risk Prediction Procedures with Censored Survival Data by Uno et al 2011. [math]\displaystyle{ \begin{align} C(\tau) = UnoC(\hat{\pi}, \tau) = \frac{\sum_{i,i'}(\hat{S}_C(t_i))^{-2}I(t_i \lt t_{i'}, t_i \lt \tau) I(\hat{\pi}_i \gt \hat{\pi}_{i'}) \delta_i}{\sum_{i,i'}(\hat{S}_C(t_i))^{-2}I(t_i \lt t_{i'}, t_i \lt \tau) \delta_i} \end{align} }[/math], a measure of the concordance between [math]\displaystyle{ \hat{\pi}_i }[/math] (the linear predictor) and the survival time.
    • real data 1: fit a Cox model. Get risk scores [math]\displaystyle{ \hat{\beta}'Z }[/math]. Compute the point and confidence interval estimates (M=500 indep. random samples with the same sample size as the observation data) of [math]\displaystyle{ C_\tau }[/math] for different [math]\displaystyle{ \tau }[/math]. Compare them with the conventional C-index procedure (Korn).
    • real data 1: compute [math]\displaystyle{ C_\tau }[/math] for a full model and a reduce model. Compute the difference of them ([math]\displaystyle{ C_\tau^{(A)} - C_\tau^{(B)} = .01 }[/math]) and the 95% confidence interval (-0.00, .02) of the difference for testing the importance of some variable (HDL in this case). Though HDL is quite significant (p=0) with respect to the risk of CV disease but its incremental value evaluated via C-statistics is quite modest.
    • real data 2: goal - evaluate the prognostic value of a new gene signature in predicting the time to death or metastasis for breast cancer patients. Two models were fitted; one with age+ER and the other is gene+age+ER. For each model we can calculate the point and interval estimates of [math]\displaystyle{ C_\tau }[/math] for different [math]\displaystyle{ \tau }[/math]s.
    • simulation: T is from Weibull regression for case 1 and log-normal regression for case 2. Covariates = (age, ER, gene). 3 kinds of censoring were considered. Sample size is 100, 150, 200 and 300. 1000 iterations. Compute coverage probabilities and average length of 95% confidence intervals, bias and root mean square error for [math]\displaystyle{ \tau }[/math] equals to 10 and 15. Compared with the conventional approach, the new method has higher coverage probabilities and less bias in 6 scenarios.
  • Statistical methods for the assessment of prognostic biomarkers (Part I): Discrimination by Tripep et al 2010
  • Assessment of Discrimination in Survival Analysis (C-statistics, etc) by anonymous
  • Uno's C-statistics
    • UnoC() from the survAUC package. It can take new data. The tau parameter: Truncation time. The resulting C tells how well the given prediction model works in predicting events that occur in the time range from 0 to tau. Con: no confidence interval estimate for [math]\displaystyle{ C_\tau }[/math] nor [math]\displaystyle{ C_\tau^{(A)} - C_\tau^{(B)} }[/math].
    • Est.Cval() from the survC1 package (authored by H. Uno). It doesn't take new data. Pro: Inf.Cval() can compute the CI of [math]\displaystyle{ C_\tau }[/math] & Inf.Cval.Delta() for the difference [math]\displaystyle{ C_\tau^{(A)} - C_\tau^{(B)} }[/math].
library(survAUC)
# require training and predict sets
TR <- ovarian[1:16,]
TE <- ovarian[17:26,]
train.fit  <- coxph(Surv(futime, fustat) ~ age, data=TR)

lpnew <- predict(train.fit, newdata=TE)
Surv.rsp <- Surv(TR$futime, TR$fustat)
Surv.rsp.new <- Surv(TE$futime, TE$fustat)              

UnoC(Surv.rsp, Surv.rsp.new, lpnew)
# [1] 0.7333333
UnoC(Surv.rsp, Surv.rsp.new, lpnew, time=365.25*5)
# [1] 0.7333333
UnoC(Surv.rsp, Surv.rsp, train.fit$linear.predictors, time=365.25*1) 
# [1] 0.9761905
UnoC(Surv.rsp, Surv.rsp, train.fit$linear.predictors, time=365.25*2) 
# [1] 0.7308979
UnoC(Surv.rsp, Surv.rsp, train.fit$linear.predictors, time=365.25*3) 
# [1] 0.7308979
UnoC(Surv.rsp, Surv.rsp, train.fit$linear.predictors, time=365.25*4) 
# [1] 0.7308979
UnoC(Surv.rsp, Surv.rsp, train.fit$linear.predictors, time=365.25*5) 
# [1] 0.7308979
# So the function UnoC() can obtain the exact result as Est.Cval().

library(survC1)
# tau is mandatory (>0), no need to have training and predict sets
Est.Cval(ovarian[1:16, c(1,2, 3)], tau=365.25*1)$Dhat
# [1] 0.9761905
Est.Cval(ovarian[1:16, c(1,2, 3)], tau=365.25*2)$Dhat
# [1] 0.7308979
Est.Cval(ovarian[1:16, c(1,2, 3)], tau=365.25*3)$Dhat
# [1] 0.7308979
Est.Cval(ovarian[1:16, c(1,2, 3)], tau=365.25*4)$Dhat
# [1] 0.7308979
Est.Cval(ovarian[1:16, c(1,2, 3)], tau=365.25*5)$Dhat
# [1] 0.7308979

Time dependent ROC curves

tdrocc()

Prognostic markers vs predictive markers

More

Logistic regression

Simulate binary data from the logistic model

https://stats.stackexchange.com/questions/46523/how-to-simulate-artificial-data-for-logistic-regression 

set.seed(666)
x1 = rnorm(1000)           # some continuous variables 
x2 = rnorm(1000)
z = 1 + 2*x1 + 3*x2        # linear combination with a bias
pr = 1/(1+exp(-z))         # pass through an inv-logit function
y = rbinom(1000,1,pr)      # bernoulli response variable
 
#now feed it to glm:
df = data.frame(y=y,x1=x1,x2=x2)
glm( y~x1+x2,data=df,family="binomial")

Building a Logistic Regression model from scratch

https://www.analyticsvidhya.com/blog/2015/10/basics-logistic-regression

Odds ratio

Calculate the odds ratio from the coefficient estimates; see this post. 

require(MASS)
N  <- 100               # generate some data
X1 <- rnorm(N, 175, 7)
X2 <- rnorm(N,  30, 8)
X3 <- abs(rnorm(N, 60, 30))
Y  <- 0.5*X1 - 0.3*X2 - 0.4*X3 + 10 + rnorm(N, 0, 12)

# dichotomize Y and do logistic regression
Yfac   <- cut(Y, breaks=c(-Inf, median(Y), Inf), labels=c("lo", "hi"))
glmFit <- glm(Yfac ~ X1 + X2 + X3, family=binomial(link="logit"))

exp(cbind(coef(glmFit), confint(glmFit)))

Medical applications

Subgroup analysis

Other related keywords: recursive partitioning, randomized clinical trials (RCT)

Statistical Learning

LDA, QDA

How to perform Logistic Regression, LDA, & QDA in R

Bagging

Chapter 8 of the book.

  • Bootstrap mean is approximately a posterior average.
  • Bootstrap aggregation or bagging average: Average the prediction over a collection of bootstrap samples, thereby reducing its variance. The bagging estimate is defined by
[math]\displaystyle{ \hat{f}_{bag}(x) = \frac{1}{B}\sum_{b=1}^B \hat{f}^{*b}(x). }[/math]

Where Bagging Might Work Better Than Boosting

Boosting

AdaBoost

AdaBoost.M1 by Freund and Schapire (1997):

The error rate on the training sample is [math]\displaystyle{ \bar{err} = \frac{1}{N} \sum_{i=1}^N I(y_i \neq G(x_i)), }[/math]

Sequentially apply the weak classification algorithm to repeatedly modified versions of the data, thereby producing a sequence of weak classifiers [math]\displaystyle{ G_m(x), m=1,2,\dots,M. }[/math]

The predictions from all of them are combined through a weighted majority vote to produce the final prediction: [math]\displaystyle{ G(x) = sign[\sum_{m=1}^M \alpha_m G_m(x)]. }[/math] Here [math]\displaystyle{ \alpha_1,\alpha_2,\dots,\alpha_M }[/math] are computed by the boosting algorithm and weight the contribution of each respective [math]\displaystyle{ G_m(x) }[/math]. Their effect is to give higher influence to the more accurate classifiers in the sequence.

Dropout regularization

DART: Dropout Regularization in Boosting Ensembles

Gradient descent

Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function (Wikipedia).

The error function from a simple linear regression looks like

[math]\displaystyle{ \begin{align} Err(m,b) &= \frac{1}{N}\sum_{i=1}^n (y_i - (m x_i + b))^2, \\ \end{align} }[/math]

We compute the gradient first for each parameters.

[math]\displaystyle{ \begin{align} \frac{\partial Err}{\partial m} &= \frac{2}{n} \sum_{i=1}^n -x_i(y_i - (m x_i + b)), \\ \frac{\partial Err}{\partial b} &= \frac{2}{n} \sum_{i=1}^n -(y_i - (m x_i + b)) \end{align} }[/math]

The gradient descent algorithm uses an iterative method to update the estimates using a tuning parameter called learning rate. 

new_m &= m_current - (learningRate * m_gradient) 
new_b &= b_current - (learningRate * b_gradient)

After each iteration, derivative is closer to zero. Coding in R for the simple linear regression.

Classification and Regression Trees (CART)

Construction of the tree classifier

  • Node proportion
[math]\displaystyle{ p(1|t) + \dots + p(6|t) =1 }[/math] where [math]\displaystyle{ p(j|t) }[/math] define the node proportions (class proportion of class j on node t. Here we assume there are 6 classes.
  • Impurity of node t
[math]\displaystyle{ i(t) }[/math] is a nonnegative function [math]\displaystyle{ \phi }[/math] of the [math]\displaystyle{ p(1|t), \dots, p(6|t) }[/math] such that [math]\displaystyle{ \phi(1/6,1/6,\dots,1/6) }[/math] = maximumm [math]\displaystyle{ \phi(1,0,\dots,0)=0, \phi(0,1,0,\dots,0)=0, \dots, \phi(0,0,0,0,0,1)=0 }[/math]. That is, the node impurity is largest when all classes are equally mixed together in it, and smallest when the node contains only one class.
  • Gini index of impurity
[math]\displaystyle{ i(t) = - \sum_{j=1}^6 p(j|t) \log p(j|t). }[/math]
  • Goodness of the split s on node t
[math]\displaystyle{ \Delta i(s, t) = i(t) -p_Li(t_L) - p_Ri(t_R). }[/math] where [math]\displaystyle{ p_R }[/math] are the proportion of the cases in t go into the left node [math]\displaystyle{ t_L }[/math] and a proportion [math]\displaystyle{ p_R }[/math] go into right node [math]\displaystyle{ t_R }[/math].

A tree was grown in the following way: At the root node [math]\displaystyle{ t_1 }[/math], a search was made through all candidate splits to find that split [math]\displaystyle{ s^* }[/math] which gave the largest decrease in impurity;

[math]\displaystyle{ \Delta i(s^*, t_1) = \max_{s} \Delta i(s, t_1). }[/math]
  • Class character of a terminal node was determined by the plurality rule. Specifically, if [math]\displaystyle{ p(j_0|t)=\max_j p(j|t) }[/math], then t was designated as a class [math]\displaystyle{ j_0 }[/math] terminal node.

R packages

Supervised Classification, Logistic and Multinomial

Variable selection and variable importance plot

Variable selection and cross-validation

Variable selection for mode regression

http://www.tandfonline.com/doi/full/10.1080/02664763.2017.1342781 Chen & Zhou, Journal of applied statistics ,June 2017

Neural network

Support vector machine (SVM)

Quadratic Discriminant Analysis (qda), KNN

Machine Learning. Stock Market Data, Part 3: Quadratic Discriminant Analysis and KNN

Regularization

Regularization is a process of introducing additional information in order to solve an ill-posed problem or to prevent overfitting

Lasso/glmnet

  • Glmnet Vignette. It tries to minimize [math]\displaystyle{ RSS(\beta) + \lambda [(1-\alpha)||\beta||_2^2/2 + \alpha ||\beta||_1] }[/math]. The elastic-net penalty is controlled by [math]\displaystyle{ \alpha }[/math], and bridge the gap between lasso ([math]\displaystyle{ \alpha = 1 }[/math]) and ridge ([math]\displaystyle{ \alpha = 0 }[/math]). Following is a CV curve (adaptive lasso) using the example from glmnet(). 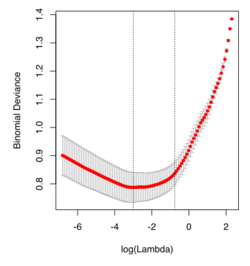Glmnetplot.svg
set.seed(1010)
n=1000;p=100
nzc=trunc(p/10)
x=matrix(rnorm(n*p),n,p)
beta=rnorm(nzc)
fx= x[,seq(nzc)] %*% beta
eps=rnorm(n)*5
y=drop(fx+eps)
px=exp(fx)
px=px/(1+px)
ly=rbinom(n=length(px),prob=px,size=1)

## Full lasso
set.seed(999)
cv.full <- cv.glmnet(x, ly, family='binomial', alpha=1, parallel=TRUE)
plot(cv.full)
log(cv.full$lambda.min) # -4.546394
log(cv.full$lambda.1se) # -3.61605
sum(coef(cv.full, s=cv.full$lambda.min) != 0) # 44

## Ridge Regression to create the Adaptive Weights Vector
set.seed(999)
cv.ridge <- cv.glmnet(x, ly, family='binomial', alpha=0, parallel=TRUE)
wt <- 1/abs(matrix(coef(cv.ridge, s=cv.ridge$lambda.min)
                   [, 1][2:(ncol(x)+1)] ))^1 ## Using gamma = 1, exclude intercept
## Adaptive Lasso
set.seed(999)
cv.lasso <- cv.glmnet(x, ly, family='binomial', alpha=1, parallel=TRUE, penalty.factor=wt)
# defautl type.measure="deviance" for logistic regression
plot(cv.lasso)
log(cv.lasso$lambda.min) # -2.995375
log(cv.lasso$lambda.1se) # -0.7625655
sum(coef(cv.lasso, s=cv.lasso$lambda.min) != 0) # 34

Ridge regression

Since L2 norm is used in the regularization, ridge regression is also called L2 regularization.

ridge regression with glmnet

Imbalanced Classification

Deep Learning

Tensor Flow (tensorflow package)

Biological applications

Bootstrap

Cross Validation

R packages:

.632 bootstrap

What is the .632 bootstrap?

Create partitions

set.seed(), sample.split(),createDataPartition(), and createFolds() functions.

k-fold cross validation with modelr and broom

Nested resampling

Nested resampling is need when we want to tuning a model by using a grid search. The default settings of a model are likely not optimal for each data set out. So an inner CV has to be performed with the aim to find the best parameter set of a learner for each fold.

See a diagram at https://i.stack.imgur.com/vh1sZ.png

In BRB-ArrayTools -> class prediction with multiple methods, the alpha (significant level of threshold used for gene selection, 2nd option in individual genes) can be viewed as a tuning parameter for the development of a classifier.

Pre-validation

Clustering

k-means clustering

Hierarchical clustering

For the kth cluster, define the Error Sum of Squares as [math]\displaystyle{ ESS_m = }[/math] sum of squared deviations (squared Euclidean distance) from the cluster centroid. [math]\displaystyle{ ESS_m = \sum_{l=1}^{n_m}\sum_{k=1}^p (x_{ml,k} - \bar{x}_{m,k})^2 }[/math] in which [math]\displaystyle{ \bar{x}_{m,k} = (1/n_m) \sum_{l=1}^{n_m} x_{ml,k} }[/math] the mean of the mth cluster for the kth variable, [math]\displaystyle{ x_{ml,k} }[/math] being the score on the kth variable [math]\displaystyle{ (k=1,\dots,p) }[/math] for the lth object [math]\displaystyle{ (l=1,\dots,n_m) }[/math] in the mth cluster [math]\displaystyle{ (m=1,\dots,g) }[/math].

If there are C clusters, define the Total Error Sum of Squares as Sum of Squares as [math]\displaystyle{ ESS = \sum_m ESS_m, m=1,\dots,C }[/math]

Consider the union of every possible pair of clusters.

Combine the 2 clusters whose combination combination results in the smallest increase in ESS.

Comments:

  1. Ward's method tends to join clusters with a small number of observations, and it is strongly biased toward producing clusters with the same shape and with roughly the same number of observations.
  2. It is also very sensitive to outliers. See Milligan (1980).

Take pomeroy data (7129 x 90) for an example: 

library(gplots)

lr = read.table("C:/ArrayTools/Sample datasets/Pomeroy/Pomeroy -Project/NORMALIZEDLOGINTENSITY.txt")
lr = as.matrix(lr)
method = "average" # method <- "complete"; method <- "ward.D"; method <- "ward.D2"
hclust1 <- function(x) hclust(x, method= method)
heatmap.2(lr, col=bluered(75), hclustfun = hclust1, distfun = dist,
              density.info="density", scale = "none",               
              key=FALSE, symkey=FALSE, trace="none", 
              main = method)

Hc ave.png Hc com.png Hc ward.png

Density based clustering

http://www.r-exercises.com/2017/06/10/density-based-clustering-exercises/

Optimal number of clusters

Mixed Effect Model

Model selection criteria

Assessing the Accuracy of our models (R Squared, Adjusted R Squared, RMSE, MAE, AIC)

Overfitting

How to judge if a supervised machine learning model is overfitting or not?

Entropy

Definition

Entropy is defined by -log2(p) where p is a probability. Higher entropy represents higher unpredictable of an event.

Some examples:

  • Fair 2-side die: Entropy = -.5*log2(.5) - .5*log2(.5) = 1.
  • Fair 6-side die: Entropy = -6*1/6*log2(1/6) = 2.58
  • Weighted 6-side die: Consider pi=.1 for i=1,..,5 and p6=.5. Entropy = -5*.1*log2(.1) - .5*log2(.5) = 2.16 (less unpredictable than a fair 6-side die).

Use

When entropy was applied to the variable selection, we want to select a class variable which gives a largest entropy difference between without any class variable (compute entropy using response only) and with that class variable (entropy is computed by adding entropy in each class level) because this variable is most discriminative and it gives most information gain. For example,

  • entropy (without any class)=.94,
  • entropy(var 1) = .69,
  • entropy(var 2)=.91,
  • entropy(var 3)=.725.

We will choose variable 1 since it gives the largest gain (.94 - .69) compared to the other variables (.94 -.91, .94 -.725).

Why is picking the attribute with the most information gain beneficial? It reduces entropy, which increases predictability. A decrease in entropy signifies an decrease in unpredictability, which also means an increase in predictability.

Consider a split of a continuous variable. Where should we cut the continuous variable to create a binary partition with the highest gain? Suppose cut point c1 creates an entropy .9 and another cut point c2 creates an entropy .1. We should choose c2.

Related

In addition to information gain, gini (dʒiːni) index is another metric used in decision tree. See wikipedia page about decision tree learning.

Ensembles

Combining classifiers. Pro: better classification performance. Con: time consuming.

Comic http://flowingdata.com/2017/09/05/xkcd-ensemble-model/

Bagging

Draw N bootstrap samples and summary the results (averaging for regression problem, majority vote for classification problem). Decrease variance without changing bias. Not help much with underfit or high bias models.

Random forest

Variance importance: if you scramble the values of a variable, and the accuracy of your tree does not change much, then the variable is not very important.

Why is it useful to compute variance importance? So the model's predictions are easier to interpret (not improve the prediction performance).

Random forest has advantages of easier to run in parallel and suitable for small n large p problems.

Boosting

Instead of selecting data points randomly with the boostrap, it favors the misclassified points.

Algorithm:

  • Initialize the weights
  • Repeat
    • resample with respect to weights
    • retrain the model
    • recompute weights

Since boosting requires computation in iterative and bagging can be run in parallel, bagging has an advantage over boosting when the data is very large.

Time series

Ensemble learning for time series forecasting in R

p-values

p-values

Distribution of p values in medical abstracts

nominal p-value and Empirical p-values

  • Nominal p-values are based on asymptotic null distributions
  • Empirical p-values are computed from simulations/permutations

(nominal) alpha level

Conventional methodology for statistical testing is, in advance of undertaking the test, to set a NOMINAL ALPHA CRITERION LEVEL (often 0.05). The outcome is classified as showing STATISTICAL SIGNIFICANCE if the actual ALPHA (probability of the outcome under the null hypothesis) is no greater than this NOMINAL ALPHA CRITERION LEVEL.

T-statistic

Let [math]\displaystyle{ \scriptstyle\hat\beta }[/math] be an estimator of parameter β in some statistical model. Then a t-statistic for this parameter is any quantity of the form

[math]\displaystyle{ t_{\hat{\beta}} = \frac{\hat\beta - \beta_0}{\mathrm{s.e.}(\hat\beta)}, }[/math]

where β0 is a non-random, known constant, and [math]\displaystyle{ \scriptstyle s.e.(\hat\beta) }[/math] is the standard error of the estimator [math]\displaystyle{ \scriptstyle\hat\beta }[/math].

Two sample test assuming equal variance

The t statistic to test whether the means are different can be calculated as follows:

[math]\displaystyle{ t = \frac{\bar {X}_1 - \bar{X}_2}{s_{X_1X_2} \cdot \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} }[/math]

where

[math]\displaystyle{ s_{X_1X_2} = \sqrt{\frac{(n_1-1)s_{X_1}^2+(n_2-1)s_{X_2}^2}{n_1+n_2-2}}. }[/math]

[math]\displaystyle{ s_{X_1X_2} }[/math] is an estimator of the common/pooled standard deviation of the two samples. The square-root of a pooled variance estimator is known as a pooled standard deviation.

The degrees of freedom is :[math]\displaystyle{ n_1 + n_2 - 2. }[/math]

Two sample test assuming unequal variance

The t statistic (Behrens-Welch test statistic) to test whether the population means are different is calculated as:

[math]\displaystyle{ t = {\overline{X}_1 - \overline{X}_2 \over s_{\overline{X}_1 - \overline{X}_2}} }[/math]

where

[math]\displaystyle{ s_{\overline{X}_1 - \overline{X}_2} = \sqrt{{s_1^2 \over n_1} + {s_2^2 \over n_2}}. }[/math]

Here s2 is the unbiased estimator of the variance of the two samples.

The degrees of freedom is evaluated using the Satterthwaite's approximation

[math]\displaystyle{ df = { ({s_1^2 \over n_1} + {s_2^2 \over n_2})^2 \over {({s_1^2 \over n_1})^2 \over n_1-1} + {({s_2^2 \over n_2})^2 \over n_2-1} }. }[/math]

Unpooled vs pooled methods

Paired test

Have you ever asked yourself, "how should I approach the classic pre-post analysis?"

Z-value/Z-score

If the population parameters are known, then rather than computing the t-statistic, one can compute the z-score.

Nonparametric test: Wilcoxon rank sum test

Sensitive to differences in location

Nonparametric test: Kolmogorov-Smirnov test

Sensitive to difference in shape and location of the distribution functions of two groups

Empirical Bayes method

See Bioconductor's limma, RnBeads, IMA, minfi packages.

ANOVA

TukeyHSD, diagnostic checking

https://datascienceplus.com/one-way-anova-in-r/

  • TukeyHSD for the pairwise tests
  • Shapiro-Wilk test for normality
  • Bartlett test and Levene test for the homogeneity of variances across the groups

Cross-over Repeated Measure Designs

https://onlinecourses.science.psu.edu/stat502/node/206

Sample Size

Goodness of fit

Chi-square tests

Contingency Tables

Odds ratio and Risk ratio

The ratio of the odds of an event occurring in one group to the odds of it occurring in another group 

         drawn   | not drawn | 
-------------------------------------
white |   A      |   B       | Wh
-------------------------------------
black |   C      |   D       | Bk
  • Odds Ratio = (A / C) / (B / D) = (AD) / (BC)
  • Risk Ratio = (A / Wh) / (C / Bk)

Hypergeometric, One-tailed Fisher exact test

         drawn   | not drawn | 
-------------------------------------
white |   x      |           | m
-------------------------------------
black |  k-x     |           | n
-------------------------------------
      |   k      |           | m+n

For example, k=100, m=100, m+n=1000, 

> 1 - phyper(10, 100, 10^3-100, 100, log.p=F)
[1] 0.4160339
> a <- dhyper(0:10, 100, 10^3-100, 100)
> cumsum(rev(a))
  [1] 1.566158e-140 1.409558e-135 3.136408e-131 3.067025e-127 1.668004e-123 5.739613e-120 1.355765e-116
  [8] 2.325536e-113 3.018276e-110 3.058586e-107 2.480543e-104 1.642534e-101  9.027724e-99  4.175767e-96
 [15]  1.644702e-93  5.572070e-91  1.638079e-88  4.210963e-86  9.530281e-84  1.910424e-81  3.410345e-79
 [22]  5.447786e-77  7.821658e-75  1.013356e-72  1.189000e-70  1.267638e-68  1.231736e-66  1.093852e-64
 [29]  8.900857e-63  6.652193e-61  4.576232e-59  2.903632e-57  1.702481e-55  9.240350e-54  4.650130e-52
 [36]  2.173043e-50  9.442985e-49  3.820823e-47  1.441257e-45  5.074077e-44  1.669028e-42  5.134399e-41
 [43]  1.478542e-39  3.989016e-38  1.009089e-36  2.395206e-35  5.338260e-34  1.117816e-32  2.200410e-31
 [50]  4.074043e-30  7.098105e-29  1.164233e-27  1.798390e-26  2.617103e-25  3.589044e-24  4.639451e-23
 [57]  5.654244e-22  6.497925e-21  7.042397e-20  7.198582e-19  6.940175e-18  6.310859e-17  5.412268e-16
 [64]  4.377256e-15  3.338067e-14  2.399811e-13  1.626091e-12  1.038184e-11  6.243346e-11  3.535115e-10
 [71]  1.883810e-09  9.442711e-09  4.449741e-08  1.970041e-07  8.188671e-07  3.193112e-06  1.167109e-05
 [78]  3.994913e-05  1.279299e-04  3.828641e-04  1.069633e-03  2.786293e-03  6.759071e-03  1.525017e-02
 [85]  3.196401e-02  6.216690e-02  1.120899e-01  1.872547e-01  2.898395e-01  4.160339e-01  5.550192e-01
 [92]  6.909666e-01  8.079129e-01  8.953150e-01  9.511926e-01  9.811343e-01  9.942110e-01  9.986807e-01
 [99]  9.998018e-01  9.999853e-01  1.000000e+00

# Density plot
plot(0:100, dhyper(0:100, 100, 10^3-100, 100), type='h')

Dhyper.svg

Moreover, 

  1 - phyper(q=10, m, n, k) 
= 1 - sum_{x=0}^{x=10} phyper(x, m, n, k)
= 1 - sum(a[1:11]) # R's index starts from 1.

Another example is the data from the functional annotation tool in DAVID. 

               | gene list | not gene list | 
-------------------------------------------------------
pathway        |   3  (q)  |               | 40 (m)
-------------------------------------------------------
not in pathway |  297      |               | 29960 (n)
-------------------------------------------------------
               |  300 (k)  |               | 30000

The one-tailed p-value from the hypergeometric test is calculated as 1 - phyper(3-1, 40, 29960, 300) = 0.0074.

Fisher's exact test

Following the above example from the DAVID website, the following R command calculates the Fisher exact test for independence in 2x2 contingency tables. 

> fisher.test(matrix(c(3, 40, 297, 29960), nr=2)) #  alternative = "two.sided" by default

        Fisher's Exact Test for Count Data

data:  matrix(c(3, 40, 297, 29960), nr = 2)
p-value = 0.008853
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
  1.488738 23.966741
sample estimates:
odds ratio
  7.564602

> fisher.test(matrix(c(3, 40, 297, 29960), nr=2), alternative="greater")

        Fisher's Exact Test for Count Data

data:  matrix(c(3, 40, 297, 29960), nr = 2)
p-value = 0.008853
alternative hypothesis: true odds ratio is greater than 1
95 percent confidence interval:
 1.973   Inf
sample estimates:
odds ratio
  7.564602

> fisher.test(matrix(c(3, 40, 297, 29960), nr=2), alternative="less")

        Fisher's Exact Test for Count Data

data:  matrix(c(3, 40, 297, 29960), nr = 2)
p-value = 0.9991
alternative hypothesis: true odds ratio is less than 1
95 percent confidence interval:
  0.00000 20.90259
sample estimates:
odds ratio
  7.564602

From the documentation of fisher.test 

Usage:
     fisher.test(x, y = NULL, workspace = 200000, hybrid = FALSE,
                 control = list(), or = 1, alternative = "two.sided",
                 conf.int = TRUE, conf.level = 0.95,
                 simulate.p.value = FALSE, B = 2000)
  • For 2 by 2 cases, p-values are obtained directly using the (central or non-central) hypergeometric distribution.
  • For 2 by 2 tables, the null of conditional independence is equivalent to the hypothesis that the odds ratio equals one.
  • The alternative for a one-sided test is based on the odds ratio, so ‘alternative = "greater"’ is a test of the odds ratio being bigger than ‘or’.
  • Two-sided tests are based on the probabilities of the tables, and take as ‘more extreme’ all tables with probabilities less than or equal to that of the observed table, the p-value being the sum of such probabilities.

GSEA

Determines whether an a priori defined set of genes shows statistically significant, concordant differences between two biological states

Two categories of GSEA procedures:

  • Competitive: compare genes in the test set relative to all other genes.
  • Self-contained: whether the gene-set is more DE than one were to expect under the null of no association between two phenotype conditions (without reference to other genes in the genome). For example the method by Jiang & Gentleman Bioinformatics 2007

Confidence vs Credibility Intervals

http://freakonometrics.hypotheses.org/18117

Power Analysis

Power analysis for default Bayesian t-tests

http://daniellakens.blogspot.com/2016/01/power-analysis-for-default-bayesian-t.html

Using simulation for power analysis: an example based on a stepped wedge study design

https://www.rdatagen.net/post/using-simulation-for-power-analysis-an-example/

Power analysis and sample size calculation for Agriculture

http://r-video-tutorial.blogspot.com/2017/07/power-analysis-and-sample-size.html

Power calculation for proportions (shiny app)

https://juliasilge.shinyapps.io/power-app/

Common covariance structures

See psu.edu

  • Diagonal structure
  • Compound symmetry
  • Toeplitz structure
  • First-order autoregressive AR(1) structure
  • Spatial Power
  • Unstructured Covariance

Counter/Special Examples

Correlated does not imply independence

Suppose X is a normally-distributed random variable with zero mean. Let Y = X^2. Clearly X and Y are not independent: if you know X, you also know Y. And if you know Y, you know the absolute value of X.

The covariance of X and Y is 

  Cov(X,Y) = E(XY) - E(X)E(Y) = E(X^3) - 0*E(Y) = E(X^3)
           = 0,

because the distribution of X is symmetric around zero. Thus the correlation r(X,Y) = Cov(X,Y)/Sqrt[Var(X)Var(Y)] = 0, and we have a situation where the variables are not independent, yet have (linear) correlation r(X,Y) = 0.

This example shows how a linear correlation coefficient does not encapsulate anything about the quadratic dependence of Y upon X.

Spearman vs Pearson correlation

Pearson benchmarks linear relationship, Spearman benchmarks monotonic relationship. https://stats.stackexchange.com/questions/8071/how-to-choose-between-pearson-and-spearman-correlation 

x=(1:100);  
y=exp(x);                        
cor(x,y, method='spearman') # 1
cor(x,y, method='pearson')  # .25

Spearman vs Wilcoxon

By this post

  • Wilcoxon used to compare categorical versus non-normal continuous variable
  • Spearman's rho used to compare two continuous (including ordinal) variables that one or both aren't normally distributed

Anscombe quartet

Four datasets have almost same properties: same mean in X, same mean in Y, same variance in X, (almost) same variance in Y, same correlation in X and Y, same linear regression.

Anscombe's quartet 3.svg

The real meaning of spurious correlations

https://nsaunders.wordpress.com/2017/02/03/the-real-meaning-of-spurious-correlations/ 

library(ggplot2)
 
set.seed(123)
spurious_data <- data.frame(x = rnorm(500, 10, 1),
                            y = rnorm(500, 10, 1),
                            z = rnorm(500, 30, 3))
cor(spurious_data$x, spurious_data$y)
# [1] -0.05943856
spurious_data %>% ggplot(aes(x, y)) + geom_point(alpha = 0.3) + 
theme_bw() + labs(title = "Plot of y versus x for 500 observations with N(10, 1)")

cor(spurious_data$x / spurious_data$z, spurious_data$y / spurious_data$z)
# [1] 0.4517972
spurious_data %>% ggplot(aes(x/z, y/z)) + geom_point(aes(color = z), alpha = 0.5) +
 theme_bw() + geom_smooth(method = "lm") + 
scale_color_gradientn(colours = c("red", "white", "blue")) + 
labs(title = "Plot of y/z versus x/z for 500 observations with x,y N(10, 1); z N(30, 3)")

spurious_data$z <- rnorm(500, 30, 6)
cor(spurious_data$x / spurious_data$z, spurious_data$y / spurious_data$z)
# [1] 0.8424597
spurious_data %>% ggplot(aes(x/z, y/z)) + geom_point(aes(color = z), alpha = 0.5) + 
theme_bw() + geom_smooth(method = "lm") + 
scale_color_gradientn(colours = c("red", "white", "blue")) + 
labs(title = "Plot of y/z versus x/z for 500 observations with x,y N(10, 1); z N(30, 6)")

Time series

Structural change

Structural Changes in Global Warming

Dictionary

  • Prognosis is the probability that an event or diagnosis will result in a particular outcome.

Following

Retrieved from "https://wiki.taichimd.us/index.php?title=Statistics&oldid=15646"