Statistics

Boxcox transformation

Finding transformation for normal distribution

Visualize the random effects

http://www.quantumforest.com/2012/11/more-sense-of-random-effects/

Sensitivity/Specificity/Accuracy

		Predict
		1	0
True	1	TP	FN	Sens=TP/(TP+FN)
	0	FP	TN	Spec=TN/(FP+TN)
				N = TP + FP + FN + TN

• Sensitivity = TP / (TP + FN)
• Specificity = TN / (TN + FP)
• Accuracy = (TP + TN) / N

Elements of Statistical Learning

Bagging

Chapter 8 of the book.

• Bootstrap mean is approximately a posterior average.
• Bootstrap aggregation or bagging average: Average the prediction over a collection of bootstrap samples, thereby reducing its variance. The bagging estimate is defined by

[math]\displaystyle{ \hat{f}_{bag}(x) = \frac{1}{B}\sum_{b=1}^B \hat{f}^{*b}(x). }[/math]

Boosting

AdaBoost.M1 by Freund and Schapire (1997):

The error rate on the training sample is [math]\displaystyle{ \bar{err} = \frac{1}{N} \sum_{i=1}^N I(y_i \neq G(x_i)), }[/math]

Sequentially apply the weak classification algorithm to repeatedly modified versions of the data, thereby producing a sequence of weak classifiers [math]\displaystyle{ G_m(x), m=1,2,\dots,M. }[/math]

The predictions from all of them are combined through a weighted majority vote to produce the final prediction: [math]\displaystyle{ G(x) = sign[\sum_{m=1}^M \alpha_m G_m(x)]. }[/math] Here [math]\displaystyle{ \alpha_1,\alpha_2,\dots,\alpha_M }[/math] are computed by the boosting algorithm and weight the contribution of each respective [math]\displaystyle{ G_m(x) }[/math]. Their effect is to give higher influence to the more accurate classifiers in the sequence.

Hierarchical clustering

For the kth cluster, define the Error Sum of Squares as [math]\displaystyle{ ESS_m = }[/math] sum of squared deviations (squared Euclidean distance) from the cluster centroid. [math]\displaystyle{ ESS_m = \sum_{l=1}^{n_m}\sum_{k=1}^p (x_{ml,k} - \bar{x}_{m,k})^2 }[/math] in which [math]\displaystyle{ \bar{x}_{m,k} = (1/n_m) \sum_{l=1}^{n_m} x_{ml,k} }[/math] the mean of the mth cluster for the kth variable, [math]\displaystyle{ x_{ml,k} }[/math] being the score on the kth variable (k=1,\dots,p)</math> for the lth object [math]\displaystyle{ (l=1,\dots,n_m) }[/math] in the mth cluster [math]\displaystyle{ (m=1,\dots,g) }[/math].

If there are C clusters, define the Total Error Sum of Squares as Sum of Squares as [math]\displaystyle{ ESS = \sum_m ESS_m, for m=1,\dots,C }[/math]

Consider the union of every possible pair of clusters.

Combine the 2 clusters whose combination combination results in the smallest increase in ESS.

Comments:

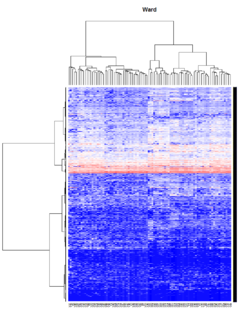
1. Ward's method tends to join clusters with a small number of observations, and it is strongly biased toward producing clusters with the same shape and with roughly the same number of observations.
2. It is also very sensitive to outliers. See Milligan (1980).

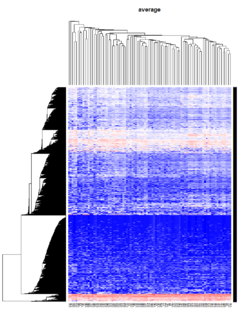
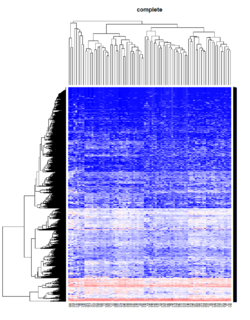
Take pomeroy data (7129 x 90) for an example:

library(gplots)

lr = read.table("C:/ArrayTools/Sample datasets/Pomeroy/Pomeroy -Project/NORMALIZEDLOGINTENSITY.txt")
lr = as.matrix(lr)
method = "average" # method <- "complete"; method <- "ward"
hclust1 <- function(x) hclust(x, method= method)
heatmap.2(lr, col=bluered(75), hclustfun = hclust1, distfun = dist,
              density.info="density", scale = "none",               
              key=FALSE, symkey=FALSE, trace="none", 
              main = method)