Statistics

BoxCox transformation

Finding transformation for normal distribution

Principal component analysis

R source code

> stats:::prcomp.default
function (x, retx = TRUE, center = TRUE, scale. = FALSE, tol = NULL, 
    ...) 
{
    x <- as.matrix(x)
    x <- scale(x, center = center, scale = scale.)
    cen <- attr(x, "scaled:center")
    sc <- attr(x, "scaled:scale")
    if (any(sc == 0)) 
        stop("cannot rescale a constant/zero column to unit variance")
    s <- svd(x, nu = 0)
    s$d <- s$d/sqrt(max(1, nrow(x) - 1))
    if (!is.null(tol)) {
        rank <- sum(s$d > (s$d[1L] * tol))
        if (rank < ncol(x)) {
            s$v <- s$v[, 1L:rank, drop = FALSE]
            s$d <- s$d[1L:rank]
        }
    }
    dimnames(s$v) <- list(colnames(x), paste0("PC", seq_len(ncol(s$v))))
    r <- list(sdev = s$d, rotation = s$v, center = if (is.null(cen)) FALSE else cen, 
        scale = if (is.null(sc)) FALSE else sc)
    if (retx) 
        r$x <- x %*% s$v
    class(r) <- "prcomp"
    r
}
<bytecode: 0x000000003296c7d8>
<environment: namespace:stats>

Related to SVD

Uusing the SVD to perform PCA makes much better sense numerically than forming the covariance matrix to begin with, since the formation of XX⊤ can cause loss of precision.

http://math.stackexchange.com/questions/3869/what-is-the-intuitive-relationship-between-svd-and-pca

Calculated by Hand

http://strata.uga.edu/software/pdf/pcaTutorial.pdf

Visualization based on simulated data

http://oracledmt.blogspot.com/2007/06/way-cooler-pca-and-visualization-linear.html

What does it do if we choose center=FALSE in prcomp()?

In USArrests data, use center=FALSE gives a better scatter plot of the first 2 PCA components.

x1 = prcomp(USArrests) 
x2 = prcomp(USArrests, center=F)
plot(x1$x[,1], x1$x[,2])  # looks random
windows(); plot(x2$x[,1], x2$x[,2]) # looks good in some sense

Visualize the random effects

http://www.quantumforest.com/2012/11/more-sense-of-random-effects/

Sensitivity/Specificity/Accuracy

		Predict
		1	0
True	1	TP	FN	Sens=TP/(TP+FN)
	0	FP	TN	Spec=TN/(FP+TN)
				N = TP + FP + FN + TN

• Sensitivity = TP / (TP + FN)
• Specificity = TN / (TN + FP)
• Accuracy = (TP + TN) / N

Generalized Linear Model

Lectures from a course in Simon Fraser University Statistics. Quasi-likelihood is on lecture 20.

Elements of Statistical Learning

Bagging

Chapter 8 of the book.

• Bootstrap mean is approximately a posterior average.
• Bootstrap aggregation or bagging average: Average the prediction over a collection of bootstrap samples, thereby reducing its variance. The bagging estimate is defined by

[math]\displaystyle{ \hat{f}_{bag}(x) = \frac{1}{B}\sum_{b=1}^B \hat{f}^{*b}(x). }[/math]

Boosting

AdaBoost.M1 by Freund and Schapire (1997):

The error rate on the training sample is [math]\displaystyle{ \bar{err} = \frac{1}{N} \sum_{i=1}^N I(y_i \neq G(x_i)), }[/math]

Sequentially apply the weak classification algorithm to repeatedly modified versions of the data, thereby producing a sequence of weak classifiers [math]\displaystyle{ G_m(x), m=1,2,\dots,M. }[/math]

The predictions from all of them are combined through a weighted majority vote to produce the final prediction: [math]\displaystyle{ G(x) = sign[\sum_{m=1}^M \alpha_m G_m(x)]. }[/math] Here [math]\displaystyle{ \alpha_1,\alpha_2,\dots,\alpha_M }[/math] are computed by the boosting algorithm and weight the contribution of each respective [math]\displaystyle{ G_m(x) }[/math]. Their effect is to give higher influence to the more accurate classifiers in the sequence.

Classification and Regression Trees (CART)

Construction of the tree classifier

• Node proportion

[math]\displaystyle{ p(1|t) + \dots + p(6|t) =1 }[/math] where [math]\displaystyle{ p(j|t) }[/math] define the node proportions (class proportion of class j on node t. Here we assume there are 6 classes.

• Impurity of node t

[math]\displaystyle{ i(t) }[/math] is a nonnegative function [math]\displaystyle{ \phi }[/math] of the [math]\displaystyle{ p(1|t), \dots, p(6|t) }[/math] such that [math]\displaystyle{ \phi(1/6,1/6,\dots,1/6) }[/math] = maximumm [math]\displaystyle{ \phi(1,0,\dots,0)=0, \phi(0,1,0,\dots,0)=0, \dots, \phi(0,0,0,0,0,1)=0 }[/math]. That is, the node impurity is largest when all classes are equally mixed together in it, and smallest when the node contains only one class.

• Gini index of impurity

[math]\displaystyle{ i(t) = - \sum_{j=1}^6 p(j|t) \log p(j|t). }[/math]

• Goodness of the split s on node t

[math]\displaystyle{ \Delta i(s, t) = i(t) -p_Li(t_L) - p_Ri(t_R). }[/math] where [math]\displaystyle{ p_R }[/math] are the proportion of the cases in t go into the left node [math]\displaystyle{ t_L }[/math] and a proportion [math]\displaystyle{ p_R }[/math] go into right node [math]\displaystyle{ t_R }[/math].

A tree was grown in the following way: At the root node [math]\displaystyle{ t_1 }[/math], a search was made through all candidate splits to find that split [math]\displaystyle{ s^* }[/math] which gave the largest decrease in impurity;

[math]\displaystyle{ \Delta i(s^*, t_1) = \max_{s} \Delta i(s, t_1). }[/math]

• Class character of a terminal node was determined by the plurality rule. Specifically, if [math]\displaystyle{ p(j_0|t)=\max_j p(j|t) }[/math], then t was designated as a class [math]\displaystyle{ j_0 }[/math] terminal node.

R packages

• rpart
• http://exploringdatablog.blogspot.com/2013/04/classification-tree-models.html

Hierarchical clustering

For the kth cluster, define the Error Sum of Squares as [math]\displaystyle{ ESS_m = }[/math] sum of squared deviations (squared Euclidean distance) from the cluster centroid. [math]\displaystyle{ ESS_m = \sum_{l=1}^{n_m}\sum_{k=1}^p (x_{ml,k} - \bar{x}_{m,k})^2 }[/math] in which [math]\displaystyle{ \bar{x}_{m,k} = (1/n_m) \sum_{l=1}^{n_m} x_{ml,k} }[/math] the mean of the mth cluster for the kth variable, [math]\displaystyle{ x_{ml,k} }[/math] being the score on the kth variable [math]\displaystyle{ (k=1,\dots,p) }[/math] for the lth object [math]\displaystyle{ (l=1,\dots,n_m) }[/math] in the mth cluster [math]\displaystyle{ (m=1,\dots,g) }[/math].

If there are C clusters, define the Total Error Sum of Squares as Sum of Squares as [math]\displaystyle{ ESS = \sum_m ESS_m, m=1,\dots,C }[/math]

Consider the union of every possible pair of clusters.

Combine the 2 clusters whose combination combination results in the smallest increase in ESS.

Comments:

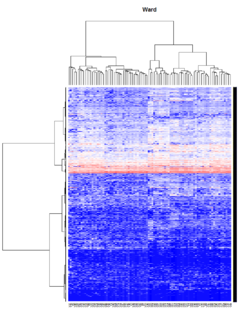
1. Ward's method tends to join clusters with a small number of observations, and it is strongly biased toward producing clusters with the same shape and with roughly the same number of observations.
2. It is also very sensitive to outliers. See Milligan (1980).

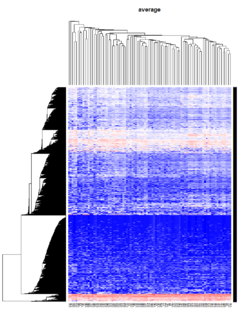
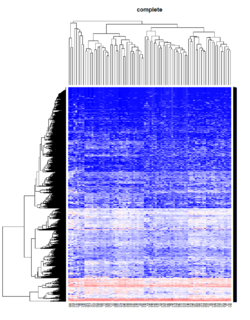
Take pomeroy data (7129 x 90) for an example:

library(gplots)

lr = read.table("C:/ArrayTools/Sample datasets/Pomeroy/Pomeroy -Project/NORMALIZEDLOGINTENSITY.txt")
lr = as.matrix(lr)
method = "average" # method <- "complete"; method <- "ward"
hclust1 <- function(x) hclust(x, method= method)
heatmap.2(lr, col=bluered(75), hclustfun = hclust1, distfun = dist,
              density.info="density", scale = "none",               
              key=FALSE, symkey=FALSE, trace="none", 
              main = method)

Mixed Effect Model

• Paper by Laird and Ware 1982
• John Fox's Linear Mixed Models Appendix to An R and S-PLUS Companion to Applied Regression. Very clear. It provides 2 typical examples (hierarchical data and longitudinal data) of using the mixed effects model. It also uses Trellis plots to examine the data.
• Chapter 10 Random and Mixed Effects from Modern Applied Statistics with S by Venables and Ripley.
• (Book) lme4: Mixed-effects modeling with R by Douglas Bates.
• (Book) Mixed-effects modeling in S and S-Plus by José Pinheiro and Douglas Bates.

Entropy

Definition

Entropy is defined by -log2(p) where p is a probability. Higher entropy represents higher unpredictable of an event.

Some examples:

• Fair 2-side die: Entropy = -.5*log2(.5) - .5*log2(.5) = 1.
• Fair 6-side die: Entropy = -6*1/6*log2(1/6) = 2.58
• Weighted 6-side die: Consider pi=.1 for i=1,..,5 and p6=.5. Entropy = -5*.1*log2(.1) - .5*log2(.5) = 2.16 (less unpredictable than a fair 6-side die).

Use

When entropy was applied to the variable selection, we want to select a class variable which gives a largest entropy difference between without any class variable (compute entropy using response only) and with that class variable (entropy is computed by adding entropy in each class level) because this variable is most discriminative and it gives most information gain. For example,

• entropy (without any class)=.94,
• entropy(var 1) = .69,
• entropy(var 2)=.91,
• entropy(var 3)=.725.

We will choose variable 1 since it gives the largest gain (.94 - .69) compared to the other variables (.94 -.91, .94 -.725).

Why is picking the attribute with the most information gain beneficial? It reduces entropy, which increases predictability. A decrease in entropy signifies an decrease in unpredictability, which also means an increase in predictability.

Consider a split of a continuous variable. Where should we cut the continuous variable to create a binary partition with the highest gain? Suppose cut point c1 creates an entropy .9 and another cut point c2 creates an entropy .1. We should choose c2.

Related

In addition to information gain, gini (dʒiːni) index is another metric used in decision tree. See wikipedia page about decision tree learning.

Ensembles

Combining classifiers. Pro: better classification performance. Con: time consuming.

Bagging

Draw N bootstrap samples and summary the results (averaging for regression problem, majority vote for classification problem). Decrease variance without changing bias. Not help much with underfit or high bias models.

Random forest

Variance importance: if you scramble the values of a variable, and the accuracy of your tree does not change much, then the variable is not very important.

Why is it useful to compute variance importance? So the model's predictions are easier to interpret (not improve the prediction performance).

Random forest has advantages of easier to run in parallel and suitable for small n large p problems.

Boosting

Instead of selecting data points randomly with the boostrap, it favors the misclassified points.

Algorithm:

• Initialize the weights
• Repeat
  • resample with respect to weights
  • retrain the model
  • recompute weights

Since boosting requires computation in iterative and bagging can be run in parallel, bagging has an advantage over boosting when the data is very large.

Counter Examples

Correlated does not imply independence

Suppose X is a normally-distributed random variable with zero mean. Let Y = X^2. Clearly X and Y are not independent: if you know X, you also know Y. And if you know Y, you know the absolute value of X.

The covariance of X and Y is

  Cov(X,Y) = E(XY) - E(X)E(Y) = E(X^3) - 0*E(Y) = E(X^3)
           = 0, 

because the distribution of X is symmetric around zero. Thus the correlation r(X,Y) = Cov(X,Y)/Sqrt[Var(X)Var(Y)] = 0, and we have a situation where the variables are not independent, yet have (linear) correlation r(X,Y) = 0.

This example shows how a linear correlation coefficient does not encapsulate anything about the quadratic dependence of Y upon X.