ICC: Difference between revisions
(→Basic) |
(→Basic) |
||
| Line 2: | Line 2: | ||
ICC: '''intra-class correlation''' | ICC: '''intra-class correlation''' | ||
* [https://dcricollab.dcri.duke.edu/sites/NIHKR/KR/Intraclass_Correlation_Coefficient_Cheat_Sheet_March_15_2020.pdf Intraclass Correlation Coefficient Cheat Sheet] | * [https://dcricollab.dcri.duke.edu/sites/NIHKR/KR/Intraclass_Correlation_Coefficient_Cheat_Sheet_March_15_2020.pdf Intraclass Correlation Coefficient Cheat Sheet] | ||
** The intraclass correlation coefficient (ICC) is a descriptive statistic that describes the extent to which outcomes 1) within each <span style="color: red">cluster</span> are likely to be similar or 2) between different <span style="color: red">clusters</span> are likely to be different from each other, relative to outcomes from other clusters. | |||
* https://en.wikipedia.org/wiki/Intraclass_correlation ('''the random effect <math>\alpha_j</math> in the one-way random model should be subjects, not raters''') | * https://en.wikipedia.org/wiki/Intraclass_correlation ('''the random effect <math>\alpha_j</math> in the one-way random model should be subjects, not raters''') | ||
** For the 1st 2 dot plots on the wikipedia, y-axis is | ** For the 1st 2 dot plots on the wikipedia, y-axis is raters values, x-axis is <span style="color: red">groups</span>. However in the R package such as like '''irr''', rows = subjects, columns = raters. | ||
** In the 3 scenario scatterplots on the wikipedia, x-axis represents rater 1 & y-axis represents rater 2. Different points represent different subjects. | ** In the 3 scenario scatterplots on the wikipedia, x-axis represents rater 1 & y-axis represents rater 2. Different points represent different subjects. | ||
** measure the '''reliability/consistency/agreement''' of | ** measure the '''reliability/consistency/agreement''' of ratings in studies where there are two or more <span style="color: red">raters</span> (主角). | ||
** It describes how strongly units in the same <span style="color: red">group</span> resemble each other. | ** It describes how strongly units in the same <span style="color: red">group</span> resemble each other. So the dot plots shown on the wikipedia should be rotated in order to match with the row/column meaning in the real data matrix. | ||
** (Early def of ICC) In the case of paired data (N groups, each group has 2 values), The key difference between this ICC and the interclass (Pearson) correlation is that the data are pooled to estimate the mean and variance. The reason for this is that in the setting where an intraclass correlation is desired, the pairs are considered to be unordered. | ** (Early def of ICC) In the case of paired data (N groups, each group has 2 values), The key difference between this ICC and the interclass (Pearson) correlation is that the data are pooled to estimate the mean and variance. The reason for this is that in the setting where an intraclass correlation is desired, the pairs are considered to be unordered. | ||
** [https://www.statisticshowto.com/intraclass-correlation/ Intraclass Correlation] from Statistics How To | ** [https://www.statisticshowto.com/intraclass-correlation/ Intraclass Correlation] from Statistics How To | ||
** [https://pdfs.semanticscholar.org/b8d4/7b0c0b12dd77543e82e6bf6636ddd335cfea.pdf Shrout, P.E., Fleiss, J.L. (1979), Intraclass correlation: uses in assessing rater reliability, Psychological Bulletin, 86, 420-428.] | ** [https://pdfs.semanticscholar.org/b8d4/7b0c0b12dd77543e82e6bf6636ddd335cfea.pdf Shrout, P.E., Fleiss, J.L. (1979), Intraclass correlation: uses in assessing rater reliability, Psychological Bulletin, 86, 420-428.] | ||
** ICC(1,1): each <span style="color: | ** ICC(1,1): each <span style="color: green">subject</span> is measured by a different set of k randomly selected <span style="color: red">raters<span>?; | ||
** ICC(2,1): k <span style="color: | ** ICC(2,1): k <span style="color: red">raters</span> are randomly selected, then, each <span style="color: green">subject</span> is measured by the same set of k raters; | ||
** ICC(3,1): similar to ICC(2,1) but k <span style="color: | ** ICC(3,1): similar to ICC(2,1) but k <span style="color: red">raters</span> are fixed. | ||
* (Modern ICC definitions) <math> | * (Modern ICC definitions) <math> | ||
Y_{ij} = \mu + \alpha_i + \varepsilon_{ij}, | Y_{ij} = \mu + \alpha_i + \varepsilon_{ij}, | ||
</math> where <math>\alpha_i</math> is the random effect from | </math> where <math>\alpha_i</math> is the random effect from <span style="color: red">'''group'''</span>, | ||
: <math> | : <math> | ||
ICC(1,1) = \frac{\sigma_\alpha^2}{\sigma_\alpha^2+\sigma_\varepsilon^2}. | ICC(1,1) = \frac{\sigma_\alpha^2}{\sigma_\alpha^2+\sigma_\varepsilon^2}. | ||
</math> | </math> | ||
: '''The intraclass correlation is the ratio of the variance attributable to subjects divided by the total of subject and error variances.''' See also the formula and estimation [https://www.uvm.edu/~statdhtx/StatPages/icc/icc.html here]. The intuition can be found in [https://stats.stackexchange.com/a/287391 examples] where the 1st case has large <math>\sigma_\alpha^2</math> and the other does not. | : '''The intraclass correlation is the ratio of the variance attributable to subjects divided by the total of subject and error variances.''' See also the formula and estimation [https://www.uvm.edu/~statdhtx/StatPages/icc/icc.html here]. The intuition can be found in [https://stats.stackexchange.com/a/287391 examples] where the 1st case has large <math>\sigma_\alpha^2</math> and the other does not. | ||
* [https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0219854 *Intraclass correlation – A discussion and demonstration of basic features] Liljequist, PLOS One 2019. It gives a good comprehensive review with formulas (including a derivation of expected mean square relations) and some simulation studies. The [https://journals.plos.org/plosone/article/figure?id=10.1371/journal.pone.0219854.g001 table] also shows the differences of '''agreement''' and '''consistency'''. | * [https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0219854 *Intraclass correlation – A discussion and demonstration of basic features] Liljequist, PLOS One 2019. It gives a good comprehensive review with formulas (including a derivation of expected mean square relations) and some simulation studies. The [https://journals.plos.org/plosone/article/figure?id=10.1371/journal.pone.0219854.g001 table] also shows the differences of '''agreement''' and '''consistency'''. | ||
* [https://www.sciencedirect.com/science/article/pii/S1556370716000158 A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research] Koo 2016. | * [https://www.sciencedirect.com/science/article/pii/S1556370716000158 A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research] Koo 2016. | ||
| Line 32: | Line 32: | ||
== Interpretation == | == Interpretation == | ||
* [https://www.statology.org/intraclass-correlation-coefficient/ Intraclass Correlation Coefficient: Definition + Example] we’d like to measure the absolute agreement among <span style="color: green">judges</span>. ... An ICC of 0.782 indicates that the exams can be rated with “good” reliability by different <span style="color: green">raters</span>. | * [https://www.statology.org/intraclass-correlation-coefficient/ Intraclass Correlation Coefficient: Definition + Example] we’d like to measure the absolute agreement among <span style="color: green">judges</span>. ... An ICC of 0.782 indicates that the exams can be rated with “good” reliability by different <span style="color: green">raters</span>. | ||
== Derive from Correlation == | |||
* The reason ICC(1,1) defined above is '''intraclass correlation <math>Corr(Y_{ij}, Y_{ik})</math>''' which can be derived here: [https://www.sas.com/content/dam/SAS/en_ca/User%20Group%20Presentations/Health-User-Groups/Maki-InterraterReliability-Apr2014.pdf Calculating the Intraclass Correlation Coefficient (ICC) in SAS]. ''Excellent!!'' For continuous data, ICC often used to assess interrater reliability. | |||
== Random intercept model == | == Random intercept model == | ||
Revision as of 14:56, 14 November 2023
Basic
ICC: intra-class correlation
- Intraclass Correlation Coefficient Cheat Sheet
- The intraclass correlation coefficient (ICC) is a descriptive statistic that describes the extent to which outcomes 1) within each cluster are likely to be similar or 2) between different clusters are likely to be different from each other, relative to outcomes from other clusters.
- https://en.wikipedia.org/wiki/Intraclass_correlation (the random effect [math]\displaystyle{ \alpha_j }[/math] in the one-way random model should be subjects, not raters)
- For the 1st 2 dot plots on the wikipedia, y-axis is raters values, x-axis is groups. However in the R package such as like irr, rows = subjects, columns = raters.
- In the 3 scenario scatterplots on the wikipedia, x-axis represents rater 1 & y-axis represents rater 2. Different points represent different subjects.
- measure the reliability/consistency/agreement of ratings in studies where there are two or more raters (主角).
- It describes how strongly units in the same group resemble each other. So the dot plots shown on the wikipedia should be rotated in order to match with the row/column meaning in the real data matrix.
- (Early def of ICC) In the case of paired data (N groups, each group has 2 values), The key difference between this ICC and the interclass (Pearson) correlation is that the data are pooled to estimate the mean and variance. The reason for this is that in the setting where an intraclass correlation is desired, the pairs are considered to be unordered.
- Intraclass Correlation from Statistics How To
- Shrout, P.E., Fleiss, J.L. (1979), Intraclass correlation: uses in assessing rater reliability, Psychological Bulletin, 86, 420-428.
- ICC(1,1): each subject is measured by a different set of k randomly selected raters?;
- ICC(2,1): k raters are randomly selected, then, each subject is measured by the same set of k raters;
- ICC(3,1): similar to ICC(2,1) but k raters are fixed.
- (Modern ICC definitions) [math]\displaystyle{ Y_{ij} = \mu + \alpha_i + \varepsilon_{ij}, }[/math] where [math]\displaystyle{ \alpha_i }[/math] is the random effect from group,
- [math]\displaystyle{ ICC(1,1) = \frac{\sigma_\alpha^2}{\sigma_\alpha^2+\sigma_\varepsilon^2}. }[/math]
- The intraclass correlation is the ratio of the variance attributable to subjects divided by the total of subject and error variances. See also the formula and estimation here. The intuition can be found in examples where the 1st case has large [math]\displaystyle{ \sigma_\alpha^2 }[/math] and the other does not.
- *Intraclass correlation – A discussion and demonstration of basic features Liljequist, PLOS One 2019. It gives a good comprehensive review with formulas (including a derivation of expected mean square relations) and some simulation studies. The table also shows the differences of agreement and consistency.
- A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research Koo 2016.
- Intraclass correlation coefficient vs. F-test (one-way ANOVA)?
- Good ICC, bad CV or vice-versa, how to interpret? Two examples are given show the difference of between-sample (think of using one value such as the average to represent a sample) variability and within-sample variability.
- Intraclass Correlation Coefficient in R. icc() [irr package] and the function ICC() [psych package] are considered with a simple example.
- Simulation. https://stats.stackexchange.com/q/135345 chapter 4 of this book: Headrick, T. C. (2010). Statistical simulation: Power method polynomials and other transformations. Boca Raton, FL: Chapman & Hall
- https://bookdown.org/roback/bookdown-bysh/ch-corrdata.html
- https://www.sas.com/content/dam/SAS/en_ca/User%20Group%20Presentations/Health-User-Groups/Maki-InterraterReliability-Apr2014.pdf
Interpretation
- Intraclass Correlation Coefficient: Definition + Example we’d like to measure the absolute agreement among judges. ... An ICC of 0.782 indicates that the exams can be rated with “good” reliability by different raters.
Derive from Correlation
- The reason ICC(1,1) defined above is intraclass correlation [math]\displaystyle{ Corr(Y_{ij}, Y_{ik}) }[/math] which can be derived here: Calculating the Intraclass Correlation Coefficient (ICC) in SAS. Excellent!! For continuous data, ICC often used to assess interrater reliability.
Random intercept model
- https://en.wikipedia.org/wiki/Multilevel_model#Random_intercepts_model
- A review of Longitudinal Data Analysis in R
R packages
The main input is a matrix of n subjects x p raters. Each rater is a class/group.
- psych: ICC()
- irr: icc() for one-way or two-way model. This works on my data 30k by 58. The default option gives ICC(1). It can also compute ICC(A,1)/agreement and ICC(C,1)/consistency.
- psy: icc(). No options are provided. I got an error: vector memory exhausted (limit reached?) when the data is 30k by 58.
- rptR:
Negative ICC
- Can ICC values be negative?
- Negative Values of the Intraclass Correlation Coefficient Are Not Theoretically Possible
- What to do with negative ICC values? Adjust the test or interpret it differently?
- Intraclass correlation – A discussion and demonstration of basic features on PLOS One. A negative ICC(1) is simply a bad (unfortunate) estimate. This may occur by chance, especially if the sample size (number of subjects n) is small.
Examples
psych package data
It shows ICC1 = ICC(1,1)
R> library(psych)
R> (o <- ICC(anxiety, lmer=FALSE) )
Call: ICC(x = anxiety, lmer = FALSE)
Intraclass correlation coefficients
type ICC F df1 df2 p lower bound upper bound
Single_raters_absolute ICC1 0.18 1.6 19 40 0.094 -0.0405 0.44
Single_random_raters ICC2 0.20 1.8 19 38 0.056 -0.0045 0.45
Single_fixed_raters ICC3 0.22 1.8 19 38 0.056 -0.0073 0.48
Average_raters_absolute ICC1k 0.39 1.6 19 40 0.094 -0.1323 0.70
Average_random_raters ICC2k 0.43 1.8 19 38 0.056 -0.0136 0.71
Average_fixed_raters ICC3k 0.45 1.8 19 38 0.056 -0.0222 0.73
Number of subjects = 20 Number of Judges = 3
R> library(irr)
R> (o2 <- icc(anxiety, model="oneway")) # subjects be considered as random effects
Single Score Intraclass Correlation
Model: oneway
Type : consistency
Subjects = 20
Raters = 3
ICC(1) = 0.175
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(19,40) = 1.64 , p = 0.0939
95%-Confidence Interval for ICC Population Values:
-0.077 < ICC < 0.484
R> o$results["Single_raters_absolute", "ICC"]
[1] 0.1750224
R> o2$value
[1] 0.1750224
R> icc(anxiety, model="twoway", type = "consistency")
Single Score Intraclass Correlation
Model: twoway
Type : consistency
Subjects = 20
Raters = 3
ICC(C,1) = 0.216
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(19,38) = 1.83 , p = 0.0562
95%-Confidence Interval for ICC Population Values:
-0.046 < ICC < 0.522
R> icc(anxiety, model="twoway", type = "agreement")
Single Score Intraclass Correlation
Model: twoway
Type : agreement
Subjects = 20
Raters = 3
ICC(A,1) = 0.198
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(19,39.7) = 1.83 , p = 0.0543
95%-Confidence Interval for ICC Population Values:
-0.039 < ICC < 0.494
library(magrittr)
library(tidyr)
library(ggplot2)
set.seed(1)
r1 <- round(rnorm(20, 10, 4))
r2 <- round(r1 + 10 + rnorm(20, 0, 2))
r3 <- round(r1 + 20 + rnorm(20, 0, 2))
df <- data.frame(r1, r2, r3) %>% pivot_longer(cols=1:3)
df %>% ggplot(aes(x=name, y=value)) + geom_point()
df0 <- cbind(r1, r2, r3)
icc(df0, model="oneway") # ICC(1) = -0.262 --> Negative.
# Shift can mess up the ICC. See wikipedia.
icc(df0, model="twoway", type = "consistency") # ICC(C,1) = 0.846 --> Make sense
icc(df0, model="twoway", type = "agreement") # ICC(A,1) = 0.106 --> Why?
ICC(df0)
Call: ICC(x = df0, lmer = T)
Intraclass correlation coefficients
type ICC F df1 df2 p lower bound upper bound
Single_raters_absolute ICC1 -0.26 0.38 19 40 9.9e-01 -0.3613 -0.085
Single_random_raters ICC2 0.11 17.43 19 38 2.9e-13 0.0020 0.293
Single_fixed_raters ICC3 0.85 17.43 19 38 2.9e-13 0.7353 0.920
Average_raters_absolute ICC1k -1.65 0.38 19 40 9.9e-01 -3.9076 -0.307
Average_random_raters ICC2k 0.26 17.43 19 38 2.9e-13 0.0061 0.555
Average_fixed_raters ICC3k 0.94 17.43 19 38 2.9e-13 0.8929 0.972
Number of subjects = 20 Number of Judges = 3
Wine rating
Intraclass Correlation: Multiple Approaches from David C. Howell. The data appeared on the paper by Shrout and Fleiss 1979.
library(magrittr)
library(psych); library(lme4)
rating <- matrix(c(9, 2, 5, 8,
6, 1, 3, 2,
8, 4, 6, 8,
7, 1, 2, 6,
10, 5, 6, 9,
6, 2, 4, 7), ncol=4, byrow=TRUE)
(o <- ICC(rating))
o$results[, 1:2]
# type ICC
#Single_raters_absolute ICC1 0.1657423 # match with icc(, "oneway")
#Single_random_raters ICC2 0.2897642 # match with icc(, "twoway", "agreement")
#Single_fixed_raters ICC3 0.7148415 # match with icc(, "twoway", "consistency")
#Average_raters_absolute ICC1k 0.4427981
#Average_random_raters ICC2k 0.6200510
#Average_fixed_raters ICC3k 0.9093159
# Plot
rating2 <- data.frame(rating) %>%
dplyr::bind_cols(data.frame(subj = paste0("s", 1:nrow(rating)))) %>%
tidyr::pivot_longer(1:4, names_to="group", values_to="y")
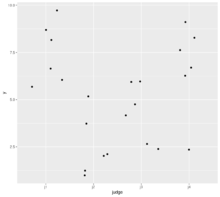
rating2 %>% ggplot(aes(x=group, y=y)) + geom_point()
library(irr) icc(rating, "oneway") # Single Score Intraclass Correlation # # Model: oneway # Type : consistency # # Subjects = 6 # Raters = 4 # ICC(1) = 0.166 # # F-Test, H0: r0 = 0 ; H1: r0 > 0 # F(5,18) = 1.79 , p = 0.165 # # 95%-Confidence Interval for ICC Population Values: # -0.133 < ICC < 0.723 icc(rating, "twoway", "agreement") # Single Score Intraclass Correlation # # Model: twoway # Type : agreement # # Subjects = 6 # Raters = 4 # ICC(A,1) = 0.29 # # F-Test, H0: r0 = 0 ; H1: r0 > 0 # F(5,4.79) = 11 , p = 0.0113 # # 95%-Confidence Interval for ICC Population Values: # 0.019 < ICC < 0.761 icc(rating, "twoway", "consistency") # Single Score Intraclass Correlation # # Model: twoway # Type : consistency # # Subjects = 6 # Raters = 4 # ICC(C,1) = 0.715 # # F-Test, H0: r0 = 0 ; H1: r0 > 0 # F(5,15) = 11 , p = 0.000135 # # 95%-Confidence Interval for ICC Population Values: # 0.342 < ICC < 0.946
anova(aov(y ~ subj + group, rating2))
# Analysis of Variance Table
#
# Response: y
# Df Sum Sq Mean Sq F value Pr(>F)
# subj 5 56.208 11.242 11.027 0.0001346 ***
# group 3 97.458 32.486 31.866 9.454e-07 ***
# Residuals 15 15.292 1.019
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(11.242 - (97.458+15.292)/18) / (11.242 + 3*(97.458+15.292)/18)
# [1] 0.165751 # ICC(1) = (BMS - WMS) / (BMS + (k-1)WMS)
# k = number of raters
(11.242 - 1.019) / (11.242 + 3*1.019 + 4*(32.486-1.019)/6)
# [1] 0.2897922 # ICC(2,1) = (BMS - EMS) / (BMS + (k-1)EMS + k(JMS-EMS)/n)
# n = number of subjects/targets
(11.242 - 1.019) / (11.242 + 3*1.019)
# [1] 0.7149451 # ICC(3,1)
Wine rating2
Intraclass correlation (from Real Statistics Using Excel) with a simple example.
R> wine <- cbind(c(1,1,3,6,6,7,8,9), c(2,3,8,4,5,5,7,9),
c(0,3,1,3,5,6,7,9), c(1,2,4,3,6,2,9,8))
R> icc(wine, model="oneway")
Single Score Intraclass Correlation
Model: oneway
Type : consistency
Subjects = 8
Raters = 4
ICC(1) = 0.728
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(7,24) = 11.7 , p = 2.18e-06
95%-Confidence Interval for ICC Population Values:
0.434 < ICC < 0.927
# For one-way random model, the order of raters is not important
R> wine2 <- wine
R> for(j in 1:8) wine2[j, ] <- sample(wine[j,])
R> icc(wine2, model="oneway")
Single Score Intraclass Correlation
Model: oneway
Type : consistency
Subjects = 8
Raters = 4
ICC(1) = 0.728
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(7,24) = 11.7 , p = 2.18e-06
95%-Confidence Interval for ICC Population Values:
0.434 < ICC < 0.927
R> icc(wine, model="twoway", type="agreement")
Single Score Intraclass Correlation
Model: twoway
Type : agreement
Subjects = 8
Raters = 4
ICC(A,1) = 0.728
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(7,24) = 11.8 , p = 2.02e-06
95%-Confidence Interval for ICC Population Values:
0.434 < ICC < 0.927
R> icc(wine, model="twoway", type="consistency")
Single Score Intraclass Correlation
Model: twoway
Type : consistency
Subjects = 8
Raters = 4
ICC(C,1) = 0.729
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(7,21) = 11.8 , p = 5.03e-06
95%-Confidence Interval for ICC Population Values:
0.426 < ICC < 0.928
Two-way fixed effects model
R> wine3 <- data.frame(wine) %>%
dplyr::bind_cols(data.frame(subj = paste0("s", 1:8))) %>%
tidyr::pivot_longer(1:4, names_to="group", values_to="y")
R> wine3 %>% ggplot(aes(x=group, y=y)) + geom_point()
R> anova(aov(y ~ subj + group, data = wine3))
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
subj 7 188.219 26.8884 11.7867 5.026e-06 ***
group 3 7.344 2.4479 1.0731 0.3818
Residuals 21 47.906 2.2813
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R> anova(aov(y ~ group + subj, data = wine3))
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
group 3 7.344 2.4479 1.0731 0.3818
subj 7 188.219 26.8884 11.7867 5.026e-06 ***
Residuals 21 47.906 2.2812
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R> library(car)
R> Anova(aov(y ~ subj + group, data = wine3))
Anova Table (Type II tests)
Response: y
Sum Sq Df F value Pr(>F)
subj 188.219 7 11.7867 5.026e-06 ***
group 7.344 3 1.0731 0.3818
Residuals 47.906 21
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Comparing intraclass correlation to Pearson correlation coefficient
Comparing intraclass correlation to Pearson correlation coefficient (with R)
In the second example (two raters, slope != 1), Pearson correlation is 1 but ICC is not large.
Is there an example where intra-class correlation ICC is large but Pearson correlation is small from two raters? One example where this can occur is when the raters are measuring the same quantity, but with different units or scales. In this case, the ICC can indicate a high level of agreement between the raters, while the Pearson correlation may not show a strong relationship between the two sets of measurements.
Cluster randomized trials
- Generating variable cluster sizes to assess power in cluster randomize trials
- A demo of power estimation by simulation for a cluster randomized trial with a time-to-event outcome
Fleiss Kappa statistic
- https://en.wikipedia.org/wiki/Fleiss%27_kappa
- Fleiss’ Kappa in R: For Multiple Categorical Variables
- It was used on the paper Comparison of pathway and gene-level models for cancer prognosis prediction Zheng 2020 to evaluate the stability of prediction models (subjects=genes/pathways, raters=replicates of CV prediction models).
Cohen's Kappa statistic
ICC and Kappa totally disagree
Concordance correlation coefficient/CCC
- https://en.wikipedia.org/wiki/Concordance_correlation_coefficient
- [math]\displaystyle{ \rho_c = \frac{2\rho\sigma_x\sigma_y}{\sigma_x^2 + \sigma_y^2 + (\mu_x - \mu_y)^2}, }[/math]
- The CCC is used to evaluate the degree of agreement between two sets of measurements or observations, and it provides a value between -1 and 1.
- The CCC is an extension of the Pearson correlation coefficient, but it takes into account not only the magnitude of the correlation between two variables but also the difference in their means. This makes it a more robust measure of agreement, especially when dealing with data that have a wide range of values or when there is a bias between the two sets of measurements.
- The CCC ranges from -1 to 1, where values close to 1 indicate strong agreement between the two sets of measurements, values close to 0 indicate no agreement, and values close to -1 indicate strong disagreement or inverse agreement. A CCC of 0.8 or higher is generally considered to indicate good agreement, while a value of less than 0.5 indicates poor agreement.
- Concordance Correlation Coefficient R-blogger
- How to compare concordance correlation coefficient to Pearson's r?
- R functions: DescTools::CCC(), yardstick::ccc(), epiR::epi.ccc()
ICC vs CCC
- Methods for evaluating the agreement between diagnostic tests Morgan 2015
- At the heart of this issue is quantifying the agreement between the results of two (or more) tests. That is, the two tests should yield similar results when applied to the same subject.
- While the paired t test could then be used to test whether the mean difference significantly differs from zero, this test cannot provide evidence that there is agreement. That is, rejecting the null hypothesis of no difference between the two sets of test results would only allow us to say that the tests do not agree; failing to reject this hypothesis would not constitute proof that the tests agree.
- M vs A plot in gene expression is an application of Bland-Altman plot. M = log2(R/G), the intensity log ratio and A is mean log intensity. The M value provides a measure of the fold change in expression between the two samples. By taking the log of the ratio of expression values, the M value is transformed into a scale that is symmetrical around zero. The log transformation of the ratio of expression values also helps to stabilize the variance of the data, making it easier to identify differentially expressed genes or transcripts between the two samples. The MA plot uses the average log expression (A value) in the x-axis because it provides a measure of the overall expression level of each gene or transcript, which is useful for identifying systematic biases in the data. See figures on SciencDirect. At each point on MA plot, M value is adjusted by subtracting the estimated bias (the height of the loess curve) at the same A value, that is, log2(R/G)=log2(R/G)−c(A), where c(A) is the lowess fit to MA plot.
- How to Create a Bland-Altman Plot in R (Step-by-Step) y=A-B, x=(A+B)/2, BlandAltmanLeh R package, y=A-B=difference, x=(A+B)/2=average.
- A simple example (Y=X+3 from wikipedia)
df <- 1:5; df <- cbind(df, df+3) cor(df[, 1], df[, 2]) # 1 library(irr) icc(df, model="twoway", type = "agreement") # Single Score Intraclass Correlation # # Model: twoway # Type : agreement # # Subjects = 5 # Raters = 2 # ICC(A,1) = 0.357 library(DescTools) CCC(df[,1], df[, 2]) # $rho.c # est lwr.ci upr.ci # 1 0.3076923 -0.0584809 0.6008884 # # $s.shift # [1] 1 # # $l.shift # [1] 2.12132 # # $C.b # [1] 0.3076923 # Note that the sample variance/covariance estimators, we use "n" as denominator 2*cov(df[, 1], df[, 2]) / (sd(df[,1])^2 + sd(df[,2])^2 + (mean(df[,1] - mean(df[,2]))^2)) # [1] 0.3571429 2*cov(df[, 1], df[, 2])*4/5 / (var(df[,1])*4/5 + var(df[,2])*4/5 + (mean(df[,1] - mean(df[,2]))^2)) [1] 0.3076923 # And if we use one-way ANOVA icc(df, model="oneway") # Single Score Intraclass Correlation # # Model: oneway # Type : consistency # # Subjects = 5 # Raters = 2 # ICC(1) = 0.0526 # Ronald Fisher n <- 5 xbar <- mean(df) s2 <- (sum((df[,1]-xbar)^2) + sum((df[,2]-xbar)^2))/ (2*n) sum( (df[,1]-xbar)*(df[,2]-xbar) ) / (n*s2) # [1] -0.05882353