Batch effect
Merging two gene expression studies
Possible batch
STAT115 Chapter 6.5 Batch Effect Removal
Visualization
- Chapter 2 Batch effect detection from the ebook Managing Batch Effects in Microbiome Data
Boxplots
X-axis is the samples and y-axis is the distributions
PCA
- Use PCA to identify batch factors
- Biological replicates can be a batch; Biological replicates consideration in DESeq2 design formula.
M vs A
MA plot for two conditions. LOESS can be applied to the data before statistical analysis. See
ComBat
- Adjusting batch effects in microarray expression data using empirical Bayes methods Johnson 2006. Note the term "ComBat" has not been used.
- Statistics for Genomic Data Science (Coursera) and https://github.com/jtleek/genstats
- Some possible batch variables: operators, runs, machines, library kits, laboratories.
- sva::ComBat() function in sva package from Bioconductor. [math]\displaystyle{ \begin{align} Y_{ijg} = \alpha_g + X \beta_g + \gamma_{ig} + \delta_{ig} \epsilon_{ijg} \end{align} }[/math] where [math]\displaystyle{ X=X_{ij} }[/math] consists of covariates (eg biological) of scientific interests (e.g. Pathway activation levels in Zhang's 2018 simulation example), while [math]\displaystyle{ \gamma_{ig} }[/math] and [math]\displaystyle{ \delta_{ig} }[/math] characterize the additive and multiplicative batch effects of batch i for gene g. The error terms, [math]\displaystyle{ \epsilon_{ijg} }[/math], are assumed to follow a normal distribution with expected value of zero and variance [math]\displaystyle{ \sigma^2_𝑔 }[/math]. The batch corrected data is [math]\displaystyle{ \begin{align} \frac{Y_{ijg} - \hat{\alpha_g} - X \hat{\beta_g} - \hat{\gamma_{ig}}}{\hat{\delta_{ig}}} + \hat{\alpha_g} + X \hat{\beta_g}. \end{align} }[/math]
- Alternative empirical Bayes models for adjusting for batch effects in genomic studies Zhang et al. BMC Bioinformatics 2018. The R package is sva and BatchQC from Bioconductor.
- Reference batch adjustment: [math]\displaystyle{ \begin{align} Y_{ijg} = \alpha_{rg} + X \beta_{rg} + \gamma_{rig} + \delta_{rig} \epsilon_{ijg} \end{align} }[/math] where [math]\displaystyle{ \alpha_{rg} }[/math] is the average gene expression in the chosen reference batch (r). Furthermore, [math]\displaystyle{ \gamma_{rig} }[/math] and [math]\displaystyle{ \delta_{rig} }[/math] represent the additive and multiplicative batch differences between the reference batch and batch i for gene g. The error terms, [math]\displaystyle{ \epsilon_{ijg} }[/math], are assumed to follow a normal distribution with expected value of zero and a reference batch variance [math]\displaystyle{ \sigma^2_{𝑟𝑔} }[/math].
- Mean-only adjustment for batch effects: [math]\displaystyle{ \begin{align} Y_{ijg} = \alpha_{g} + X \beta_{g} + \gamma_{ig} + \epsilon_{ijg} \end{align} }[/math]
- pyComBat, a Python tool for batch effects correction in high-throughput molecular data using empirical Bayes method 2023
- Q: does data from each batch after correction have the same mean and variance?
- No, the data from each batch do not necessarily have the same mean and variance after correction by ComBat. The goal of ComBat is to adjust the data so that the batch effects are removed, making the data from different batches more comparable. However, this does not mean that the mean and variance of the data from each batch will be identical after correction.
- ComBat uses empirical Bayes methods (pooling information across genes to generate more robust estimates for gene-wise mean and variance batch effect) to estimate the parameters of the Gaussian distribution (mean and variance) for each batch. These parameters are then shrunk towards a common value. The data is adjusted based on these shrunken parameters. This process helps to remove the batch effects, but it does not force the data from each batch to have the same mean and variance.
- It’s important to note that while ComBat can effectively adjust for known batch effects, it may not completely eliminate all batch effects, especially if there are unknown or unmodeled batch effects present. Therefore, it’s always important to visually inspect the data and perform additional statistical tests to confirm the effectiveness of the batch correction.
- Q: how to verify the batch effects have been corrected?
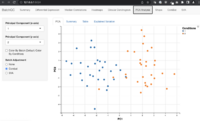
- Visual Inspection: After batch correction, you can visually inspect the data using plots such as PCA plots or t-SNE plots. The samples from different batches should overlap with each other if the batch effects have been successfully removed.
- Statistical Tests: You can perform statistical tests to check if the distribution of the data from different batches has become more similar after batch correction. For example, you can use tests such as the Kolmogorov-Smirnov test or the Anderson-Darling test.
- Correlation and Linear Fit Plots: You can follow up the conditional plot with a linear correlation plot, a linear intercept plot, a linear slope plot, and a linear residual standard deviation plot. These four plots show the correlation, the intercept and slope from a linear fit, and the residual standard deviation for linear fits applied to each batch.
- Benchmarking Metrics: Performance can be evaluated using benchmarking metrics including kBET, LISI, ASW, and ARI.
- Differential Expression Analysis: Investigate the use of batch-corrected data to study differential gene expression.
- Q: What is Bayesian estimation and Shrinkage. Empirical Bayes methods shrink the estimated parameters (eg sample mean from one gene for mean parameter) towards a common value (depending on the prior). Multiple genes/batches were used to estimate the hyperparameter. Th estimated hyperparameter was used to compute the posterior distribution of the unknown main parameter. See revisit and Understanding empirical Bayes estimation (using baseball statistics).
- Naive method:
# Step 1 data <- matrix(rnorm(1000), nrow=100) batch <- factor(rep(c(1,2), each=50)) # Step 2: estimate batch means batch_means <- tapply(1:nrow(data), batch, function(rows) colMeans(data[rows,])) # Step 3: estimate overall means overall_means <- colMeans(data) # Step 4: shrink batch means. Shrink the batch means towards the overall means. # The degree of shrinkage could be determined empirically, or set to a fixed value. shrunken_means <- (batch_means + overall_means) / 2 # Step 5; adjust data # (shrunken_means[batch[i]] - overall_means[i]) = batch effect; # the batch-specific deviation from the overall mean corrected_data <- data for(i in 1:ncol(data)) { corrected_data[,i] <- data[,i] - (shrunken_means[batch[i]] - overall_means[i]) } - svg vignette example to remove the batch effect
BiocManager::install("sva") library(sva) library(bladderbatch) data(bladderdata) pheno = pData(bladderEset) edata = exprs(bladderEset) batch = pheno$batch table(pheno$batch, pheno$cancer) table(batch) # batch # 1 2 3 4 5 # 11 18 4 5 19 modcombat = model.matrix(~1, data=pheno) combat_edata = ComBat(dat=edata, batch=batch, mod=modcombat, prior.plots=FALSE) # This returns an expression matrix, with the same dimensions # as your original dataset (genes x samples). # mod: Model matrix for outcome of interest and other covariates besides batch # By default, it performs parametric empirical Bayesian adjustments. # If you would like to use nonparametric empirical Bayesian adjustments, # use the par.prior=FALSE option (this will take longer). dim(edata) # [1] 22283 57 combat_edata = ComBat(dat=edata, batch=batch, ref.batch=1) dim(combat_edata) # [1] 22283 57Does the result change if we use a subset of samples in combat but fix the ref.batch?
Ans: the change is almost negligible(batch.sub <- batch %in% c(1,2,3,4)) # [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE FALSE TRUE # [11] FALSE TRUE FALSE TRUE FALSE FALSE TRUE TRUE FALSE TRUE # [21] TRUE TRUE TRUE FALSE TRUE TRUE FALSE TRUE TRUE TRUE # [31] TRUE TRUE TRUE FALSE TRUE TRUE TRUE TRUE TRUE TRUE # [41] FALSE FALSE FALSE TRUE FALSE TRUE FALSE FALSE TRUE TRUE # [51] FALSE FALSE FALSE FALSE TRUE TRUE TRUE combat_edata2 = ComBat(dat=edata[, batch.sub], batch=batch[batch.sub], ref.batch=1) range(combat_edata[, batch.sub] - combat_edata2) # [1] -0.00000000000004796163 0.00000000000003019807
Does the result change if we use a subset of genes?
Ans: yes, more appreciable depending on how much is the subset of genes.combat_edata3 = ComBat(dat=edata[1:20000,], batch=batch, ref.batch=1) range(combat_edata[1:20000,] - combat_edata3) # [1] -0.03803818 0.01561327 combat_edata4 = ComBat(dat=edata[1:22000,], batch=batch, ref.batch=1) range(combat_edata[1:22000,] - combat_edata4) # [1] -0.006031209 0.012482280
- ref.batch for reference-based batch adjustment. mean.only option if there is no need to adjust the variancec. Check out paper Alternative empirical Bayes models for adjusting for batch effects in genomic studies Zhang 2018. Figure 4 shows reference-based ComBat can clearly show the pathway activated samples in Batch 1 samples and show the true data pattern in Batch 2 samples from the simulated study (vs the original ComBat approach failed for both cases). In Figure 5 when we cluster genes using K-means, referenced-based Combat can better identify the role of DE or control genes (compared to the original ComBat method). In addition to the github reposition for the simulation R code, BatchQC::rnaseq_sim() can also do that.
- Merging two gene-expression studies via cross-platform normalization by Shabalin et al, Bioinformatics 2008. This method (called Cross-Platform Normalization/XPN)was used by Ternès Biometrical Journal 2017.
- Batch effect removal methods for microarray gene expression data integration: a survey by Lazar et al, Bioinformatics 2012. The R package is inSilicoMerging which has been removed from Bioconductor 3.4.
- Question: Combine hgu133a&b and hgu133plus2. Adjusting batch effects in microarray expression data using empirical Bayes methods
- Gene expression profiling of 1200 pancreatic ductal adenocarcinoma reveals novel subtypes
- Figure S1 shows the principal component analysis (PCA) before and after batch effect correction for training and validation datasets
- Batch effects and GC content of NGS by Michael Love
- 困扰的batch effect
- Some note by Mikhail Dozmorov
mod parameter
- ?ComBat. mod: Model matrix for outcome of interest and other covariates besides batch.
- The mod parameter is a design matrix, typically created using the model.matrix() function in R. It represents known biological covariates or experimental conditions that you want to protect during the batch effect correction.
- When you adjust for batch effects with ComBat(), you want to remove only the variation due to batch — not the variation due to your variables of interest (like case/control, treatment groups, etc.). The mod matrix helps ComBat() distinguish between batch effects and biological signal.
- What exactly should and shouldn't go in Combat's model matrix?
- Simulated data to demonstrate the effect of the 'mod' parameter has been ignored.

CovBat
- Mitigating site effects in covariance for machine learning in neuroimaging data Chen 2022. CovBat is a novel harmonization method called Correcting Covariance Batch Effects that removes site effects in mean, variance, and covariance. It was proposed to address the issue of differences in images acquired across multiple sites in multi-site neuroimaging studies. These differences, often referred to as site effects, have been shown to bias comparison between sites, mask biologically meaningful associations, and even introduce spurious associations. The field has focused on harmonizing data by removing site-related effects in the mean and variance of measurements, but these methods may not be sufficient for machine learning. CovBat accounts for the joint distribution of ComBat-adjusted observations.
- https://github.com/andy1764/CovBat_Harmonization
- Comprehensive evaluation of harmonization on functional brain imaging for multisite data-fusion Wang 2023
ComBat-Seq
- sva package vignette
# Example 1 count_matrix <- matrix(rnbinom(400, size=10, prob=0.1), nrow=50, ncol=8) batch <- c(rep(1, 4), rep(2, 4)) adjusted <- ComBat_seq(count_matrix, batch=batch, group=NULL) # Example 2 - one biological variable group <- rep(c(0,1), 4) adjusted_counts <- ComBat_seq(count_matrix, batch=batch, group=group) # Example 3 - multiple biological variables cov1 <- rep(c(0,1), 4) cov2 <- c(0,0,1,1,0,0,1,1) covar_mat <- cbind(cov1, cov2) adjusted_counts <- ComBat_seq(count_matrix, batch=batch, group=NULL, covar_mod=covar_mat)
- ? ComBat_seq It currently (sva version 3.44.0 as of 2022/6) does not have the ref.batch option? See this post Can you add the parameter of ref.batch in ComBat-Seq? #51. One alternative is to normalize the count data of the two batches separately first (for example, using DEseq2) and correct the batch effect then using combat.
- ComBat-seq: batch effect adjustment for RNA-seq count data 2020
- Introduction to Bioconductor SVA and ComBat-Seq in R
- Using ComBat-seq on transcript counts.
- You need to use the RSEM expected counts (values in the expected_counts column are still not integers).
- There is no need to round them to exact integers. You absolutely cannot use TPM or FPKM.
- An example of RSEM output here.
- How to use combat in order to remove batch effects? DESeq() + vst() + limma::removeBatchEffect()
- 数据分析:RNA-seq数据的批次校正方法 It includes complete R code for running ComBat_seq() including ComBat_seq(), limma+removeBatchEffect, PCA, VOOM+SNM, DESeq2.
- Evaluation of critical data processing steps for reliable prediction of gene co-expression from large collections of RNA-seq data Vandenbon 2022
svaseq
Applications
DESeq2
- Batch effects vs biological variables
- Batch Effect in DESeq2, how to control, how to remove it, how to address biological question
- Batch-correction on tximport data from salmon. Include the batch effect in the design of DESeq2. No need to use an external tool like ComBat_seq(). Search the keyword batch in the Vignette.
- Batch correction for RNA-seq didn't work with ComBat-seq tool
- How to get TPM / FPKM after batch correction with DESeq2?
- Convert uncorrected counts to FPKM (DESeq2::fpkm()) and then log2 scale and use it for Batch correction with limma::removeBatchEffect.
limma::removeBatchEffect()
- removeBatchEffect() from limma package
- Batch effects : ComBat or removebatcheffects (limma package) ?
- Tutorial:Basic normalization, batch correction and visualization of RNA-seq data
- Extracting fitted expression matrix from Limma
- How to use removeBatchEffect for removing effect of multiple confounding variables? The batch1 and batch2 arguments are really just for convenience. Everything gets combined into the covariates matrix before doing the math.
design <- model.matrix(~TREAT + A + B + C, data=covariates_df) treatment.design <- design[,1:2] batch.design <- design[,-(1:2)] corrected_vst_df <- removeBatchEffect(t(vst_df), design=treatment.design, covariates=batch.design) - how to remove batch effects of RNA seq data based on continuous variables(like surrogate variables from sva package) using combatseq or limma (removebatcheffect function)?)
ComBat or removebatcheffects (limma package)
- Batch effects : ComBat or removebatcheffects (limma package) ?
- The conclusion that you should get from reading this is that correcting for batch directly with programs like ComBat is best avoided.
- See Methods that remove batch effects while retaining group differences may lead to exaggerated confidence in downstream analyses Nygaard 2016 (215 cites vs 5372 cites from ComBat)
- batch effect : comBat or blocking in limma ?. See the comment by Evan Johnson
- correcting the batch effects in Limma and SVA answered by Gordon Smyth.
ComBat or blocking in limma
batch effect : comBat or blocking in limma ?. The main difference between what Limma does and ComBat is that ComBat adjusts for differences in both the mean and variance differences across the batches, whereas Limma (I believe--Gordon please confirm) assumes that the batch variances are the same and only accounts for mean differences across the batches. So if there are large differences in batch variances, it might still be better to use ComBat. If there are not large variance differences, then Limma should be the best.
Repeat measure
Batch correction and repeated measures. You should just do a standard limma analysis as recommended. You should not use ComBat to pre batch-correct.
Comparisons of svaseq and Combat
Evaluation of Methods in Removing Batch Effects on RNA-seq Data. The results show the SVA method has the best performance, while the ComBat method over-corrects the batch effect.
HarmonizeR, proteomic
MultiBaC- Multiomic Batch effect Correction
Review: Thinking points
Thinking points for effective batch correction on biomedical data
BatchQC tool
- https://www.bioconductor.org/packages/release/bioc/html/BatchQC.html
- What is Explained Variance? (Definition & Example)
- The explained variance can be found in the SS (“sum of squares”) column for the Between Groups variation.
- In a regression model, the explained variance is summarized by R-squared, often written R2 = SSR/SST; Coefficient of Determination.
- Some screenshots
AMDBNorm - adjustment mean distribution-based normalization
AMDBNorm: an approach based on distribution adjustment to eliminate batch effects of gene expression data Zhang, Briefings in Bioinformatics 2021
AMDBNorm assumes that each sample in the biologic condition has the same distribution.
It selects a reference batch in advance, then
- aligns other batches with the distribution of the reference batch, and finally
- corrects the gene expression according to their mean values in the reference batch so that the expression of each gene in each batch is at the same level.
Evaluation methods
- Visualization by principal component analysis
- Evaluation of batch effects by BatchQC software
- Principal variance component analysis
- Hierarchical cluster analysis
- Sensitivity analysis of AMDBNorm to reference batch
- Adaptability analysis of batch correction methods to the new samples
TCGA
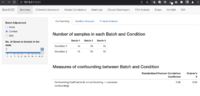
Confounding factors
- AC-PCoA: Adjustment for confounding factors using principal coordinate analysis 2022
- Controling for batch effect while preserving variation within repeated measures. Your batch and subject are (mostly) confounded.
Impute
- Why you should not use mean imputation for missing data
- The Problem: When missing values are replaced by a single constant (the mean), the imputed data points have zero deviation from the mean, which shrinks the overall spread of the data.
- The Result: The standard deviation (and thus the variance) of the imputed variable is significantly underestimated compared to the standard deviation of the observed data.
- Consequence: Since many statistical tests (like t-tests and regression) rely on variance, reducing it can lead to inflated test statistics and result in false positive conclusions (spurious significance). The simulation showed a statistically significant difference between the standard deviation of the dropped-missing-data set and the mean-imputed set.
impute.knn
- ?impute.knn impute.knn(data ,k = 10, rowmax = 0.5, colmax = 0.8, maxp = 1500, rng.seed=362436069)
- rowmax: The maximum percent missing data allowed in any row (default 50%). For any rows with more than rowmax% missing are imputed using the overall mean per sample.
- colmax: The maximum percent missing data allowed in any column (default 80%). If any column has more than colmax% missing data, the program halts and reports an error.
BiocManager::install("impute") library(impute) set.seed(1) x <- matrix(rnorm(10*4), nr=10) x[1,1] <- NA x[2,1:2] <- NA x[3,1:3] <- NA x[1:9, 1] <- NA x2 <- impute.knn(x, k=2) # Error in impute.knn(x, k = 2) : # a column has more than 80 % missing values! set.seed(1) x <- matrix(rnorm(10*4), nr=10) x[1,1] <- NA x[2,1:2] <- NA x[3,1:3] <- NA x2 <- impute.knn(x, k=2) # Warning message: # In knnimp(x, k, maxmiss = rowmax, maxp = maxp) : # 1 rows with more than 50 % entries missing; # mean imputation used for these rows names(x2) [1] "data" "rng.seed" "rng.state" head(x2$data) # [,1] [,2] [,3] [,4] # [1,] 0.1351965 1.51178117 0.91897737 1.35867955 # [2,] -0.5629284 0.27448386 0.78213630 -0.10278773 # [3,] 0.0000000 0.00000000 0.00000000 0.38767161 # [4,] 1.5952808 -2.21469989 -1.98935170 -0.05380504 # [5,] 0.3295078 1.12493092 0.61982575 -1.37705956 set.seed(1) x <- 2^matrix(rnorm(10*4), nr=10) x[1,1] <- NA x[2,1:2] <- NA x[3,1:3] <- NA x2 <- impute.knn(x, k=2) head(x2$data) x3 <- impute.knn(x, k=2) identical(x2$data, x3$data) # trueAnother case that we are able to verify imputed for rows with more than rowmax% missing values. Two rows satisfy the condition. Note the missing value on row 3, column 3 is computed by excluding ALL rows satisfying the condition.
set.seed(1) x <- matrix(rnorm(10*4), nr=10) x[1,1] <- NA x[2,1:2] <- NA x[3,1:3] <- NA x2 <- impute.knn(x, k=2, rowmax=.25) # Warning message: # In knnimp(x, k, maxmiss = rowmax, maxp = maxp) : # 2 rows with more than 25 % entries missing; # mean imputation used for these rows head(x2$data) # [,1] [,2] [,3] [,4] # [1,] 0.1351965 1.51178117 0.91897737 1.35867955 # [2,] 0.3714953 0.33998088 0.78213630 -0.10278773 # [3,] 0.3714953 0.33998088 -0.27417921 0.38767161 # [4,] 1.5952808 -2.21469989 -1.98935170 -0.05380504 mean(x[,1], na.rm = T) # [1] 0.3714953 # same mean(x[,2], na.rm = T) # [1] 0.3399809 # same mean(x[,3], na.rm = T) # [1] -0.1568108 # not the same mean(x[-c(2,3),3], na.rm = T) # [1] -0.2741792 # same x3 <- x2$data x3[1,1] <- NA dist(x3) # find row1's 2 nearest neighbors are rows9 & 10. round(as.matrix(dist(x3))[1,], 2) # 1 2 3 4 5 6 7 8 9 10 # 0.00 2.17 2.23 5.70 3.21 2.95 2.96 3.27 1.82 1.39 mean(x[9:10,1]) # [1] 0.1351965
Nearest-neighbor samples
kNN Imputation for Missing Values in Machine Learning. A new sample is imputed by finding the samples in the training set “closest” to it and averages these nearby points to fill in the value.
Proteomics data
- Comparative assessment and novel strategy on methods for imputing proteomics data Shen 2022
- As shown in Fig. 3c, NIPALS (non-linear estimation by iterative partial least squares), SVT (singular value thresholding), and protein-wise or sample-wise KNN achieve the best performance.
- A comparative study of evaluating missing value imputation methods in label-free proteomics Jin 2021