Glmnet

From 太極
Jump to navigation Jump to search

Basic

  • https://en.wikipedia.org/wiki/Lasso_(statistics). It has a discussion when two covariates are highly correlated. For example if gene [math]\displaystyle{ i }[/math] and gene [math]\displaystyle{ j }[/math] are identical, then the values of [math]\displaystyle{ \beta _{j} }[/math] and [math]\displaystyle{ \beta _{k} }[/math] that minimize the lasso objective function are not uniquely determined. Elastic Net has been designed to address this shortcoming.
    • Strongly correlated covariates have similar regression coefficients, is referred to as the grouping effect. From the wikipedia page "one would like to find all the associated covariates, rather than selecting only one from each set of strongly correlated covariates, as lasso often does. In addition, selecting only a single covariate from each group will typically result in increased prediction error, since the model is less robust (which is why ridge regression often outperforms lasso)".
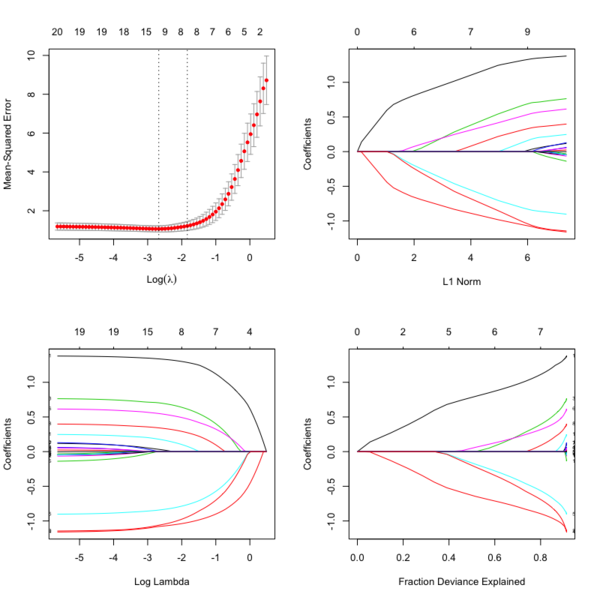
  • Glmnet Vignette. It tries to minimize [math]\displaystyle{ RSS(\beta) + \lambda [(1-\alpha)\|\beta\|_2^2/2 + \alpha \|\beta\|_1] }[/math]. The elastic-net penalty is controlled by [math]\displaystyle{ \alpha }[/math], and bridge the gap between lasso ([math]\displaystyle{ \alpha = 1 }[/math]) and ridge ([math]\displaystyle{ \alpha = 0 }[/math]). Following is a CV curve (adaptive lasso) using the example from glmnet(). Two vertical lines are indicated: left one is lambda.min (that gives minimum mean cross-validated error) and right one is lambda.1se (the most regularized model such that error is within one standard error of the minimum). For the tuning parameter [math]\displaystyle{ \lambda }[/math],
    • The larger the [math]\displaystyle{ \lambda }[/math], more coefficients are becoming zeros (think about coefficient path plots) and thus the simpler (more regularized) the model.
    • If [math]\displaystyle{ \lambda }[/math] becomes zero, it reduces to the regular regression and if [math]\displaystyle{ \lambda }[/math] becomes infinity, the coefficients become zeros.
    • In terms of the bias-variance tradeoff, the larger the [math]\displaystyle{ \lambda }[/math], the higher the bias and the lower the variance of the coefficient estimators.
  • Video by Trevor Hastie

File:Glmnetplot.svg File:Glmnet path.svg File:Glmnet l1norm.svg 

set.seed(1010)
n=1000;p=100
nzc=trunc(p/10)
x=matrix(rnorm(n*p),n,p)
beta=rnorm(nzc)
fx= x[,seq(nzc)] %*% beta
eps=rnorm(n)*5
y=drop(fx+eps)
px=exp(fx)
px=px/(1+px)
ly=rbinom(n=length(px),prob=px,size=1)

## Full lasso
library(doParallel)
registerDoParallel(cores = 2)
set.seed(999)
cv.full <- cv.glmnet(x, ly, family='binomial', alpha=1, parallel=TRUE)
plot(cv.full)  # cross-validation curve and two lambda's
plot(glmnet(x, ly, family='binomial', alpha=1), xvar="lambda", label=TRUE) # coefficient path plot
plot(glmnet(x, ly, family='binomial', alpha=1))  # L1 norm plot
log(cv.full$lambda.min) # -4.546394
log(cv.full$lambda.1se) # -3.61605
sum(coef(cv.full, s=cv.full$lambda.min) != 0) # 44

## Ridge Regression to create the Adaptive Weights Vector
set.seed(999)
cv.ridge <- cv.glmnet(x, ly, family='binomial', alpha=0, parallel=TRUE)
wt <- 1/abs(matrix(coef(cv.ridge, s=cv.ridge$lambda.min)
                   [, 1][2:(ncol(x)+1)] ))^1 ## Using gamma = 1, exclude intercept
## Adaptive Lasso using the 'penalty.factor' argument
set.seed(999)
cv.lasso <- cv.glmnet(x, ly, family='binomial', alpha=1, parallel=TRUE, 
                      penalty.factor=wt)
# defautl type.measure="deviance" for logistic regression
plot(cv.lasso)
log(cv.lasso$lambda.min) # -2.995375
log(cv.lasso$lambda.1se) # -0.7625655
sum(coef(cv.lasso, s=cv.lasso$lambda.min) != 0) # 34

Lambda [math]\displaystyle{ \lambda }[/math]

  • A list of potential lambdas: see Linear Regression case. The λ sequence is determined by lambda.max and lambda.min.ratio.
    • lambda.max is computed from the input x and y; it is the maximal value for lambda such that all the coefficients are zero. How does glmnet compute the maximal lambda value? & Choosing the range and grid density for regularization parameter in LASSO. However see the Random data example.
    • lambda.min.ratio (default is ifelse(nobs<nvars,0.01,0.0001)) is the ratio of smallest value of the generated λ sequence (say lambda.min) to lambda.max.
    • The program then generated nlambda values linear on the log scale from lambda.max down to lambda.min.
    • The sequence of lambda does not change with different data partitions from running cv.glmnet().
    • Avoid supplying a single value for lambda (for predictions after CV use predict() instead). Supply instead a decreasing sequence of lambda values. I'll get different coefficients when I use coef(cv.glmnet obj) and coef(glmnet obj). See the complete code on gist. 
      cvfit <- cv.glmnet(x, y, family = "cox", nfolds=10)
fit <- glmnet(x, y, family = "cox", lambda = lambda)
coef.cv <- coef(cvfit, s = lambda)
coef.fit <- coef(fit)
length(coef.cv[coef.cv != 0]) # 31
length(coef.fit[coef.fit != 0]) # 30
all.equal(lambda, cvfit$lambda[40])  # TRUE
length(cvfit$lambda) # [1] 100

Optimal lambda for Cox model

See Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent Simon 2011. We choose the λ value which maximizes [math]\displaystyle{ \hat{CV}(\lambda) }[/math].

[math]\displaystyle{ \begin{align} \hat{CV}_{i}(\lambda) = l(\beta_{-i}(\lambda)) - l_{-i}(\beta_{-i}(\lambda)). \end{align} }[/math]

Our total goodness of fit estimate, [math]\displaystyle{ \hat{CV}(\lambda) }[/math], is the sum of all [math]\displaystyle{ \hat{CV}_{i}(\lambda). }[/math] By using the equation above – subtracting the log-partial likelihood evaluated on the non-left out data from that evaluated on the full data – we can make efficient use of the death times of the left out data in relation to the death times of all the data.

Get the partial likelihood of a Cox PH model with new data

Random data

  • For random survival (response) data, glmnet easily returns 0 covariates by using lambda.min.
  • For random binary or quantitative trait (response) data, it seems glmnet returns at least 1 covariate at lambda.min which is max(lambda). This seems contradicts the documentation which describes all coefficients are zero with max(lambda).

See the code here.

Multiple seeds in cross-validation

  • Variablity in cv.glmnet results. From the cv.glmnet() reference manual: Note also that the results of cv.glmnet are random, since the folds are selected at random. Users can reduce this randomness by running cv.glmnet many times, and averaging the error curves. 
    MSEs <- NULL
for (i in 1:100){
                 cv <- cv.glmnet(y, x, alpha=alpha, nfolds=k)  
                 MSEs <- cbind(MSEs, cv$cvm)
             }
rownames(MSEs) <- cv$lambda
lambda.min <- as.numeric(names(which.min(rowMeans(MSEs))))
  • Stabilizing the lasso against cross-validation variability
  • caret::trainControl(.., repeats, ...)

    Cross Validated LASSO: What are its weaknesses?

    Cross Validated LASSO with the glmnet package: What are its weaknesses?

    At what lambda is each coefficient shrunk to 0

    glmnet: at what lambda is each coefficient shrunk to 0?

    Mixing parameter [math]\displaystyle{ \alpha }[/math]

    cva.glmnet() from the glmnetUtils package to choose both the alpha and lambda parameters via cross-validation, following the approach described in the help page for cv.glmnet.

    Underfittig, overfitting and relaxed lasso

    Plots

    library(glmnet)
data(QuickStartExample) # x is 100 x 20 matrix

cvfit = cv.glmnet(x, y)
fit = glmnet(x, y)

oldpar <- par(mfrow=c(2,2))
plot(cvfit) # mse vs log(lambda)
plot(fit) # coef vs L1 norm
plot(fit, xvar = "lambda", label = TRUE) # coef vs log(lambda)
plot(fit, xvar = "dev", label = TRUE) # coef vs Fraction Deviance Explained
par(oldpar)

    Glmnet4plotn.png

    print() method

    ?print.glmnet and ?print.cv.glmnet

    Extract/compute deviance

    deviance(fitted_glmnet_object)

coxnet.deviance(pred = NULL, y, x = 0, offset = NULL,
  weights = NULL, beta = NULL) # This calls a Fortran function loglike()

    According to the source code, coxnet.deviance() returns 2 *(lsat-fit$flog).

    coxnet.deviance() was used in assess.coxnet.R (CV, not intended for use by users) and buildPredmat.coxnetlist.R (CV).

    See also Survival → glmnet.

    coefplot: Plots Coefficients from Fitted Models

    cv.glmnet and deviance

    Usage 

    cv.glmnet(x, y, weights = NULL, offset = NULL, lambda = NULL,
  type.measure = c("default", "mse", "deviance", "class", "auc", "mae",
  "C"), nfolds = 10, foldid = NULL, alignment = c("lambda",
  "fraction"), grouped = TRUE, keep = FALSE, parallel = FALSE,
  gamma = c(0, 0.25, 0.5, 0.75, 1), relax = FALSE, trace.it = 0, ...)

    type.measure parameter (loss to use for CV):

    • default
      • type.measure = deviance which uses squared-error for gaussian models (a.k.a type.measure="mse"), logistic and poisson regression (PS: for binary response data I found that type='class' gives a discontinuous CV curve while 'deviance' give a smooth CV curve), deviance formula for binomial model which is the same as the formula shown here and binomial glm case.
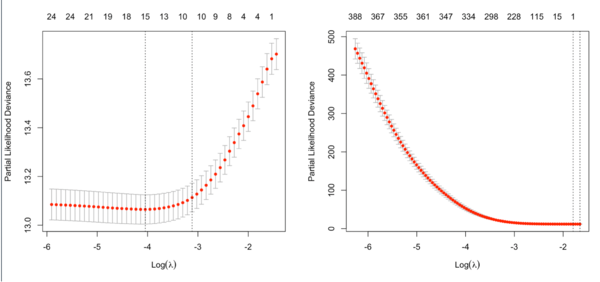
      • type.measure = partial-likelihood for the Cox model (note that the y-axis from plot.cv.glmnet() gives deviance but the values are quite different from what deviace() gives from a non-CV modelling).
    • mse or mae (mean absolute error) can be used by all models except the "cox"; they measure the deviation from the fitted mean to the response
    • class applies to binomial and multinomial logistic regression only, and gives misclassification error.
    • auc is for two-class logistic regression only, and gives area under the ROC curve. In order to calculate the AUC (which really needs a way to rank your test cases) glmnet needs at least 10 obs; see Calculate LOO-AUC values using glmnet.
    • C is Harrel's concordance measure, only available for cox models

    How to choose type.measure for binary response.

    grouped parameter

    • This is an experimental argument, with default TRUE, and can be ignored by most users.
    • For the "cox" family, grouped=TRUE obtains the CV partial likelihood for the Kth fold by subtraction; by subtracting the log partial likelihood evaluated on the full dataset from that evaluated on the on the (K-1)/K dataset. This makes more efficient use of risk sets. With grouped=FALSE the log partial likelihood is computed only on the Kth fold
    • Gradient descent for the elastic net Cox-PH model
    package deviance CV
    survival -2*fit$loglik[1]
    glmnet deviance(fit)
    assess.glmnet(fit, newx, newy, family = "cox")
    coxnet.deviance(x, y, beta)     		cv.glmnet(x, y, lambda, family="cox", nfolds, foldid)$cvm
    which calls cv.glmnet.raw() (save lasso models for each CV)
    which calls buildPredmat.coxnetlist(foldid) to create a matrix cvraw (eg 10x100)
    and then calls cv.coxnet(foldid) (it creates weights of length 10 based on status and do cvraw/=weights)
    and cvstats(foldid) which will calculate weighted mean of cvraw matrix for each lambda
    and return the cvm vector; cvm[1]=sum(original cvraw[,1])/sum(weights)
    Note: the document says the measure (cvm) is partial likelihood for survival data.
    But cvraw calculation from buildPredmat.coxnetlist() shows the original/unweighted cvraw is CVPL.
    BhGLM measure.bh(fit, new.x, new.y) cv.bh(fit, nfolds=10, foldid, ncv)$measures[1]
    which calls an internal function measure.cox(y.obj, lp) (lp is obtained from CV)
    which calls bcoxph() [coxph()] using lp as the covariate and returns
    deviance = -2 * ff$loglik[2] (a CV deviance)
    cindex = summary(ff)$concordance[[1]] (a CV c-index)

    An example from the glmnet vignette The deviance value is the same from both survival::deviance() and glmnet::deviance(). But how about cv.glmnet()$cvm (partial-likelihood)? 

    library(glmnet)
library(survival)
library(tidyverse); library(magrittr)

data(CoxExample)
dim(x) # 1000 x 30
# I'll focus some lambdas based on one run of cv.glmnet()
set.seed(1); cvfit = cv.glmnet(x, y, family = "cox", lambda=c(10,2,1,.237,.016,.003))
rbind(cvfit$lambda, cvfit$cvm,
      deviance(glmnet(x, y, family = "cox", lambda=c(10, 2, 1, .237, .016, .003))))%>% 
      set_rownames(c("lambda", "cvm", "deviance"))
               [,1]       [,2]       [,3]       [,4]       [,5]      [,6]
lambda     10.00000    2.00000    1.00000    0.23700    0.01600    0.0030
cvm        13.70484   13.70484   13.70484   13.70316   13.07713   13.1101
deviance 8177.16378 8177.16378 8177.16378 8177.16378 7707.53515 7697.3357

-2* coxph(Surv(y[,1], y[, 2]) ~ x)$loglik[1]
[1] 8177.164
coxph(Surv(y[,1], y[, 2]) ~ x)$loglik[1]
[1] -4088.582

# coxnet.deviance: compute the deviance (-2 log partial likelihood) for right-censored survival data
fit1 = glmnet(x, y, family = "cox", lambda=.016)
coxnet.deviance(x=x, y=y, beta=fit1$coef)
# [1] 8177.164
fit2 = glmnet(x, y, family = "cox", lambda=.003)
coxnet.deviance(x=x, y=y, beta=fit2$coef)
# [1] 8177.164

# assess.glmnet
assess.glmnet(fit1, newx=x, newy=y)
# $deviance
# [1] 7707.444
# attr(,"measure")
# [1] "Partial Likelihood Deviance"
#
# $C
# [1] 0.7331241
# attr(,"measure")
# [1] "C-index"

assess.glmnet(fit2, newx=x, newy=y)
# $deviance
# [1] 7697.314
# attr(,"measure")
# [1] "Partial Likelihood Deviance"
#
# $C
# [1] 0.7342417
# attr(,"measure")
# [1] "C-index"

    What deviance is glmnet using

    What deviance is glmnet using to compare values of 𝜆?

    No need for glmnet if we have run cv.glmnet

    https://stats.stackexchange.com/a/77549 Do not supply a single value for lambda. Supply instead a decreasing sequence of lambda values. glmnet relies on its warms starts for speed, and its often faster to fit a whole path than compute a single fit.

    Exact definition of Deviance measure in glmnet package, with CV

    cv.glmnet in cox model

    Note: the CV result may changes unless we fix the random seed.

    Note that the y-axis on the plot depends on the type.measure parameter. It is not the objective function used to find the estimator. For survival data, the y-axis is (residual) deviance (-2*loglikelihood, or RSS in linear regression case) [so the optimal lambda should give a minimal deviance value].

    It is not always partial likelihood device has a largest value at a large lambda. In the following two plots, the first one is from the glmnet vignette and the 2nd one is from the coxnet vignette. The survival data are not sparse in both examples.

    Cvcoxnet.png

    CVPL

    Sparse data 

    library(glmnet); library(survival)
n = 100; p <- 1000
beta1 = 2; beta2 = -1; beta3 =1; beta4 = -2
lambdaT = .002 # baseline hazard
lambdaC = .004  # hazard of censoring
set.seed(1234)
x1 = rnorm(n)
x2 = rnorm(n)
x3 <- rnorm(n)
x4 <- rnorm(n)
# true event time
T = Vectorize(rweibull)(n=1, shape=1, scale=lambdaT*exp(-beta1*x1-beta2*x2-beta3*x3-beta4*x4))
C = rweibull(n, shape=1, scale=lambdaC)   #censoring time
time = pmin(T,C)  #observed time is min of censored and true
event = time==T   # set to 1 if event is observed
cox <- coxph(Surv(time, event)~ x1 + x2 + x3 + x4); cox
-2*cox$loglik[2] # deviance [1] 301.7461
summary(cox)$concordance[1]  # 0.9006085

# create a sparse matrix
X <- cbind(x1, x2, x3, x4, matrix(rnorm(n*(p-4)), nr=n))
colnames(X) <- paste0("x", 1:p)
# X <- data.frame(X)
y <- Surv(time, event)
set.seed(1234)
nfold <- 10
foldid <- sample(rep(seq(nfold), length = n))
cvfit <- cv.glmnet(X, y, family = "cox", foldid = foldid)
plot(cvfit)
plot(cvfit$lambda, log = "y")
assess.glmnet(cvfit, newx=X, newy = y, family="cox") # return deviance 361.4619 and C 0.897421
            # Question: what lambda has been used?
            # Ans: assess.glmnet() calls predict.cv.glmnet() which by default uses s = "lambda.1se"

fit <- glmnet(X, y, family = "cox", lambda = cvfit$lambda.min)
assess.glmnet(fit, newx=X, newy = y, family="cox") # deviance 308.3646 and C 0.9382788
cvfit$cvm[cvfit$lambda == cvfit$lambda.min]
# [1] 7.959283

fit <- glmnet(X, y, family = "cox", lambda = cvfit$lambda.1se)
assess.glmnet(fit, newx=X, newy = y, family="cox") # deviance  361.4786 and C 0.897421
deviance(fit)
# [1] 361.4786

fit <- glmnet(X, y, family = "cox", lambda = 1e-3)
assess.glmnet(fit, newx=X, newy = y, family="cox") # deviance 13.33405 and C 1

fit <- glmnet(X, y, family = "cox", lambda = 1e-8)
assess.glmnet(fit, newx=X, newy = y, family="cox") # deviance 457.3695 and C .5

fit <- glmnet(cbind(x1,x2,x3,x4), y, family = "cox", lambda = 1e-8)
assess.glmnet(fit, newx=X, newy = y, family="cox")
# Error in h(simpleError(msg, call)) :
#  error in evaluating the argument 'x' in selecting a method for function 'as.matrix': Cholmod error 
#  'X and/or Y have wrong dimensions' at file ../MatrixOps/cholmod_sdmult.c, line 90
deviance(fit) # [1] 301.7462

library(BhGLM)
X2 <- data.frame(X)
f1 = bmlasso(X2, y, family = "cox",  ss = c(.04, .5))
measure.bh(f1, X2, y)
# deviance   Cindex
#   303.39     0.90

o <- cv.bh(f1, foldid = foldid)
o$measures  # deviance and C
# deviance   Cindex
#  311.743    0.895

    update() function

    update() will update and (by default) re-fit a model. It does this by extracting the call stored in the object, updating the call and (by default) evaluating that call. Sometimes it is useful to call update with only one argument, for example if the data frame has been corrected.

    It can be used in glmnet() object without a new implementation method.

    • Linear regression 
      lm(y ~ x + z, data=myData)
lm(y ~ x + z, data=subset(myData, sex=="female"))
lm(y ~ x + z, data=subset(myData, age > 30))
    • Lasso regression 
      R> fit <- glmnet(glmnet(X, y, family="cox", lambda=cvfit$lambda.min); fit
Call:  glmnet(x = X, y = y, family = "cox", lambda = cvfit$lambda.min)

  Df   %Dev Lambda
1 21 0.3002 0.1137

R> fit2 <- update(fit, subset = c(rep(T, 50), rep(F, 50)); fit2
Call:  glmnet(x = X[1:50, ], y = y[1:50], family = "cox", lambda = cvfit$lambda.min)

  Df   %Dev Lambda
1 24 0.4449 0.1137

R> fit3 <- update(fit, lambda=cvfit$lambda); fit3

Call:  glmnet(x = X, y = y, family = "cox", lambda = cvfit$lambda)

    Df    %Dev  Lambda
1    1 0.00000 0.34710
2    2 0.01597 0.33130
...

    cv.glmnet and glmnet give different coefficients

    glmnet: same lambda but different coefficients for glmnet() & cv.glmnet()

    Number of nonzero in cv.glmnet plot is not monotonic in lambda

    It is possible since this is based on CV? But if we use coef() to compute the nonzero coefficients for each lambda from the fitted model, it should be monotonic. Below is one case and the Cox regression example above is another case.

    Cvglmnetplot.png

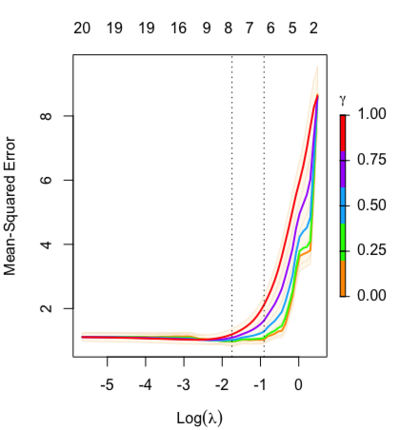
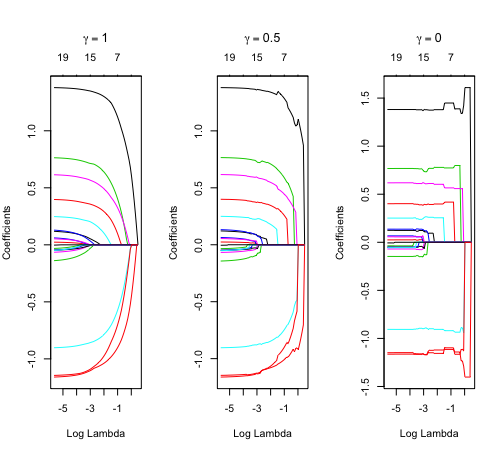
    Relaxed fit and [math]\displaystyle{ \gamma }[/math] parameter

    https://cran.r-project.org/web/packages/glmnet/vignettes/relax.pdf

    Relaxed fit: Take a glmnet fitted object, and then for each lambda, refit the variables in the active set without any penalization.

    Suppose the glmnet fitted linear predictor at [math]\displaystyle{ \lambda }[/math] is [math]\displaystyle{ \hat\eta_\lambda(x) }[/math] and the relaxed version is [math]\displaystyle{ \tilde\eta_\lambda(x) }[/math]. We also allow for shrinkage between the two:

    [math]\displaystyle{ \begin{align} \tilde \eta_{\lambda,\gamma}= \gamma\hat\eta_\lambda(x) + (1-\gamma)\tilde\eta_\lambda(x). \end{align} }[/math]

    [math]\displaystyle{ \gamma\in[0,1] }[/math] is an additional tuning parameter which can be selected by cross validation.

    The debiasing will potentially improve prediction performance, and CV will typically select a model with a smaller number of variables.

    The default behavior of extractor functions like predict and coef, as well as plot will be to present results from the glmnet fit (not cv.glmnet), unless a value of [math]\displaystyle{ \gamma }[/math] is given different from the default value [math]\displaystyle{ \gamma=1 }[/math].

    Question: how does cv.glmnet() select [math]\displaystyle{ \gamma }[/math] parameter? Ans: it depends on the parameter type.measure in cv.glmnet. 

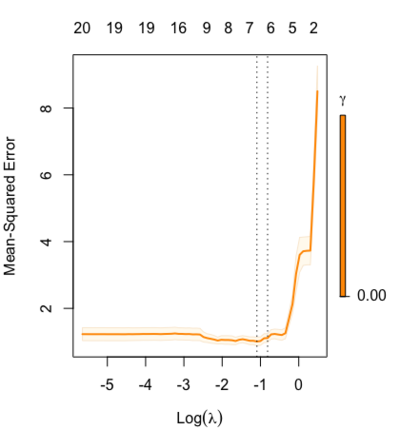
    library(glmnet)
data(QuickStartExample)
fitr=glmnet(x,y, relax=TRUE)
set.seed(1)
cfitr=cv.glmnet(x,y,relax=TRUE)
c(fitr$lambda.min, fitr$lambda.1se)
# [1] 0.08307327 0.15932708
str(cfitr$relaxed)
plot(cfitr),oldpar <- par(mfrow=c(1,3), mar = c(5,4,6,2))
plot(fitr, main = expression(gamma == 1))
plot(fitr,gamma=0.5, main = expression(gamma == .5))
plot(fitr,gamma=0, main = expression(gamma == 0))
par(oldpar)
    		Special cases:
    • [math]\displaystyle{ \gamma=1 }[/math]: only regularized fit, no relaxed fit.
    • [math]\displaystyle{ \gamma=0 }[/math]: only relaxed fit; a faster version of forward stepwise regression.
    set.seed(1)
cfitr2=cv.glmnet(x,y,gamma=0,relax=TRUE) 
  # default gamma = c(0, 0.25, 0.5, 0.75, 1)
plot(cfitr2)
c(cfitr2$lambda.min, cfitr2$lambda.1se)
# [1] 0.08307327 0.15932708
str(cfitr2$relaxed)

    Glmnetrelaxcv.png Glmnetrelaxfit.png

    Glmnetrelaxcv2.png

    Computation time

    beta1 = 2; beta2 = -1
lambdaT = .002 # baseline hazard
lambdaC = .004  # hazard of censoring
set.seed(1234)
x1 = rnorm(n)
x2 = rnorm(n)
# true event time
T = Vectorize(rweibull)(n=1, shape=1, scale=lambdaT*exp(-beta1*x1-beta2*x2)) 
# No censoring
event2 <- rep(1, length(T))

system.time(fit <- cv.glmnet(x, Surv(T,event2), family = 'cox'))
#    user  system elapsed 
#   4.701   0.016   4.721 
system.time(fitr <- cv.glmnet(x, Surv(T,event2), family = 'cox', relax= TRUE))
#    user  system elapsed 
# 161.002   0.382 161.573

    predict() and coef() methods

    ?predict.glmnet OR ?coef.glmnet OR ?coef.relaxed. Similar to other predict methods, this functions predicts fitted values, logits, coefficients and more from a fitted "glmnet" object.

    For family="binomial" (logistic model),

    • type = "response": fitted probabilities
    • type = "link": the linear predictors, e.g. beta*x
    • type = "class": class label corresponding to the maximum probability
    • type = "nonzero": a list of the indices of the nonzero coefficients for each value of 's'

    In other words, response(fitted probabilities) = exp(Link)/(1+exp(Link)) and class = 1 if response <.5 and class = 2 if response >.5. 

    ## S3 method for class 'glmnet'
predict(object, newx, s = NULL, type = c("link",
  "response", "coefficients", "nonzero", "class"), exact = FALSE,
  newoffset, ...)

## S3 method for class 'relaxed'
predict(object, newx, s = NULL, gamma = 1,
  type = c("link", "response", "coefficients", "nonzero", "class"),
  exact = FALSE, newoffset, ...)
## S3 method for class 'glmnet'
coef(object, s = NULL, exact = FALSE, ...)

    ?predict.cv.glmnet OR ?coef.cv.glmnet OR ?coef.cv.relaxed. This function makes predictions from a cross-validated glmnet model, using the stored "glmnet.fit" object, and the optimal value chosen for lambda (and gamma for a 'relaxed' fit). 

    ## S3 method for class 'cv.glmnet'
predict(object, newx, s = c("lambda.1se",
  "lambda.min"), ...)

## S3 method for class 'cv.relaxed'
predict(object, newx, s = c("lambda.1se",
  "lambda.min"), gamma = c("gamma.1se", "gamma.min"), ...)

    AUC

    Cindex

    https://www.rdocumentation.org/packages/glmnet/versions/3.0-2/topics/Cindex

    Usage: 

    Cindex(pred, y, weights = rep(1, nrow(y)))

    assess.glmnet

    https://www.rdocumentation.org/packages/glmnet/versions/3.0-2/topics/assess.glmnet

    Usage: 

    assess.glmnet(object, newx = NULL, newy, weights = NULL,
  family = c("gaussian", "binomial", "poisson", "multinomial", "cox",
  "mgaussian"), ...)
confusion.glmnet(object, newx = NULL, newy, family = c("binomial",
  "multinomial"), ...)

roc.glmnet(object, newx = NULL, newy, ...)

    Variable importance

    R-square/R2 and dev.ratio

    • How to calculate 𝑅2 for LASSO (glmnet). Use cvfit$glmnet.fit$dev.ratio. According to ?glmnet, dev.ratio is the fraction of (null) deviance explained (for "elnet", this is the R-square).
    • How to calculate R Squared value for Lasso regression using glmnet in R
    • Coefficient of determination from wikipedia. R2 is the proportion of the variation in the dependent variable that is predictable from the independent variable(s).
    • What is the main difference between multiple R-squared and correlation coefficient? It provides 4 ways (same value) to calculate R2 for multiple regression (not glmnet). 
      fm <- lm(Y ~ X1 + X2) # regression of Y on X1 and X2
fm_null <- lm(Y ~ 1)  # null model

# Method 1: definition
var(fitted(fm)) / var(Y) # ratio of variances
# Method 2
cor(fitted(fm), Y)^2 # squared correlation
# Method 3
summary(fm)$r.squared # multiple R squared
# Method 4
1 - deviance(fm) / deviance(fm_null)  # improvement in residual sum of squares
    • %Dev is R2 in linear regression case. How to calculate R Squared value for Lasso regression using glmnet in R, How to calculate 𝑅2 for LASSO (glmnet) 
      library(glmnet)
data(QuickStartExample)
x <- QuickStartExample$x
y <- QuickStartExample$y
dim(x)
# [1] 100  20

fit2 <- lm(y~x)
summary(fit2)
# Multiple R-squared:  0.9132,    Adjusted R-squared:  0.8912

glmnet(x, y)
#    Df  %Dev  Lambda
# 1   0  0.00 1.63100
# 2   2  5.53 1.48600
# 3   2 14.59 1.35400
# ...
# 64 20 91.31 0.00464
# 65 20 91.32 0.00423
# 66 20 91.32 0.00386
# 67 20 91.32 0.00351
    • An example to get R2 (deviance) from glmnet. %DEV or cv.glmnet()$glmnet.fit$dev.ratio is fraction of (null) deviance explained. ?deviance.glmnet 
      set.seed(1010)
n=1000;p=100
nzc=trunc(p/10)
x=matrix(rnorm(n*p),n,p)
beta=rnorm(nzc)
fx= x[,seq(nzc)] %*% beta
eps=rnorm(n)*5
y=drop(fx+eps)

set.seed(999)
cvfit <- cv.glmnet(x, y)
cvfit 
# Measure: Mean-Squared Error 
#     Lambda Index Measure     SE Nonzero
# min 0.2096    24   24.32 0.8105      21
# 1se 0.3663    18   24.93 0.8808      12
cvfit$cvm[cvfit$lambda == cvfit$lambda.min]
# 24.3218   <- mean cross-validated error
cvfit$glmnet.fit
#    Df  %Dev  Lambda
# 1   0  0.00 1.78100
# 2   1  1.72 1.62300
# 23 19 25.40 0.23000
# 24 21 25.96 0.20960  <- Same as glmnet() result   -----------------------------+
# 25 21 26.44 0.19100                                                            |
# ...                                                                            |
cvfit$glmnet.fit$dev.ratio[cvfit$lambda == cvfit$lambda.min]                     |
# [1] 0.2596395   dev.ratio=1-dev/nulldev. ?deviance.glmnet                      |
                                                                                 |
fit <- glmnet(x, y, lambda=cvfit$lambda.min); fit                                |
#   Df  %Dev Lambda                                                              |
# 1 21 25.96 0.2096    <---------------------------------------------------------+
predict.lasso <- predict(fit, newx=x, s="lambda.min", type = 'response')[,1]     |
                                                                                 |
1 - deviance(fit)/deviance(lm(y~1))                                              |
# [1] 0.2596395   <- Same as glmnet()  ------------------------------------------+
deviance(lm(y~1))  # Same as sum((y-mean(y))**2)
deviance(fit)      # Same as sum((y-predict.lasso)**2)
cor(predict.lasso, y)^2
# [1] 0.2714228   <- Not the same as glmnet()
var(predict.lasso) / var(y)                                       
# [1] 0.1701002   <- Not the same as glmnet()

    ridge regression and multicollinear

    https://en.wikipedia.org/wiki/Ridge_regression. Ridge regression is a method of estimating the coefficients of multiple-regression models in scenarios where linearly independent variables are highly correlated. 

    # example from SGL package
set.seed(1)
n = 50; p = 100; size.groups = 10
X = matrix(rnorm(n * p), ncol = p, nrow = n)
beta = (-2:2)
y = X[,1:5] %*% beta + 0.1*rnorm(n)
data = list(x = X, y = y)

cvfit <- cv.glmnet(X, y, alpha = 0)
plot(cvfit)

o <- coef(cvfit, lambda = cvfit$lambda.min) %>% drop()

sum(o != 0) # [1] 101. 
            # Too biased.
o[1:10] 
#   (Intercept)            V1            V2            V3            V4 
# -3.269401e-01 -2.253226e-36 -8.900799e-37  5.198885e-37  1.311976e-36 
#            V5            V6            V7            V8            V9 
#  1.873125e-36  1.582532e-37  2.085781e-37  4.732839e-37  2.997614e-37

y_predicted <- predict(cvfit, s = cvfit$lambda.min, newx = X)
# Sum of Squares Total and Error
sst <- sum((y - mean(y))^2)
sse <- sum((y_predicted - y)^2)
# R squared
rsq <- 1 - sse / sst
rsq  # 0.46

library(SGL)  # sparse group lasso
set.seed(1)
index <- ceiling(1:p / size.groups)
cvFit = cvSGL(data, index, type = "linear", alpha=.95) # this alpha is the default
plot(cvFit)
cvFit$fit$beta[, 20] # 20th lambda gives smallest negative log likelihood  
                     # identify correct predictors
#  [1] -10.942712  -6.167799   0.000000   6.595406  14.442019   0.000000 ...

set.seed(1)
cvFit2 = cvSGL(data, index, type = "linear", alpha=0)
plot(cvFit2)
cvFit2$fit$beta[, 20]
#  [1] -10.8417371  -6.5251240   0.2476438   6.7223001  14.1605263   0.2149542
#  [7]   0.2481450   0.1404282   0.1799818   0.3784596   0.0000000   0.0000000 ...
    • Tikhonov regularization (ridge regression). It was used to handle ill-posed/overfitting situation. Ridge regression shrinks the coefficients by a uniform factor of [math]\displaystyle{ {\displaystyle (1+N\lambda )^{-1}}{\displaystyle (1+N\lambda )^{-1}} }[/math] and does not set any coefficients to zero.
    • cvSGL
    • How and when: ridge regression with glmnet. On training data, ridge regression fits less well than the OLS but the parameter estimate is more stable. So it does better in prediction because it is less sensitive to extreme variance in the data such as outliers.

    Filtering variables

    See its vignette.

    One might think that unsupervised filtering using just x before fitting the model is fair game, and perhaps need not be accounted for in cross-validation. This is an interesting issue, and one can argue that there could be some bias if it was not accounted for. But filtering using x and y definitely introduces potential bias. However, it can still give good results, as long as it it correctly accounted for when running CV.

    Graphical lasso

    Group lasso

    • pcLasso: Principal Components Lasso package
      • pclasso paper, slides, Blog
      • Each feature must be assigned to a group
      • It allows to assign each feature to groups (including overlapping). 
        library(pcLasso)

set.seed(1)
n = 50; p = 100; size.groups = 10
index <- ceiling(1:p / size.groups)
X = matrix(rnorm(n * p), ncol = p, nrow = n)
beta = (-2:2)
y = X[,1:5] %*% beta + 0.1*rnorm(n)

groups <- vector("list", 3)
for (k in 1:2) {
    groups[[k]] <- 5 * (k-1) + 1:5
}
groups[[3]] <- 11:p
cvfit <- cv.pcLasso(X, y, ratio = 0.8, groups = groups)
plot(cvfit)

pred.pclasso <- predict(cvfit, xnew = X, s = "lambda.min")
mean((y-pred.pclasso)^2)  #  [1] 1.956387

library(SGL)
index <- ceiling(1:p / size.groups)
data = list(x = X, y = y)
set.seed(1)
cvFit = cvSGL(data, index, type = "linear")
Fit = SGL(data, index, type = "linear")
  # 1. SGL() uses a different set of lambdas than cvSGL() does (WHY)
  #    After looking at cvFit$lambdas; Fit$lambdas
  #    I should pick the last lambda; the smallest 
  # 2. predictSGL() source code shows Fit$X.transform$X.means
  #    and Fit$X.transform$X.scale should be applied to the new data
  #    before it calls X %*% x$beta[, lam] + intercept
  # 3. The returned values of predictSGL() depends on the response type
  #    (linear, logit or cox).
  #    For linear, it returns eta = X %*% x$beta[, lam] + intercept
  #    For logit, it returns exp(eta)/(1 + exp(eta))
  #    For cox, it returns exp(eta)
pred.SGL <- predictSGL(Fit, X, length(Fit$lambdas))
mean((y-pred.SGL)^2)    # [1] 0.146027
# Coefficients
Fit$beta[, 20]
Fit$intercept

library(ggplot2)
library(tidyr)
dat <- tibble(y=y, SGL=pred.SGL, pclasso=pred.pclasso) %>% gather("method", "predict", 2:3)

ggplot(dat, aes(x=y, y=predict, color=method)) + geom_point() + geom_abline(slope=1)

    Minimax concave penalty (MCP)

    penalty.factor

    The is available in glmnet() but not in cv.glmnet().

    Collinearity

    categorical covariates, multi-collinearity/multicollinearity, contrasts()

    • Group lasso
    • Can glmnet logistic regression directly handle factor (categorical) variables without needing dummy variables? 
      x_train <- model.matrix( ~ .-1, factor(x)) # affect encoding for the 1st level; see ?formula
cvfit = cv.glmnet(x=x_train, y=y, intercept=FALSE)
coef(cvfit, s="lambda.min") # still contains intercept but it is 0
    • GLM vs Lasso vs SGL 
      library(glmnet)
library(SGL)

set.seed(1010)
n=1000;p=100
nzc=trunc(p/10)
x=matrix(rnorm(n*p),n,p)
beta=rnorm(nzc)
tumortype <- sample(c(1:4), size = n, replace = TRUE)
fx= x[,seq(nzc)] %*% beta + .5*tumortype
eps=rnorm(n)*5
y=drop(fx+eps)
if (FALSE) {
  # binary response based on the logistic model
  px=exp(fx)
  px=px/(1+px)
  ly=rbinom(n=length(px),prob=px,size=1)
}

# glm. Assume we know the true variables.
df <- cbind(data.frame(x[, 1:10]), tumortype, y)
colnames(df) <- c(paste0("x", 1:10), "tumortype", "y")
mod <- glm(y ~ ., data = df)
broom::tidy(mod) # summary(mod)
pred.glm <- predict(mod, newdata = df)
mean((y-pred.glm)^2) # 23.32704

# lasso 1. tumortype is continuous
X <- cbind(x, tumortype)
set.seed(1234)
fit.lasso <- cv.glmnet(X, y, alpha=1)
predict.lasso1 <- predict(fit.lasso, newx=X, s="lambda.min", type = 'response')[,1]
coef.lasso1 <- coef(fit.lasso)[,1]
sum(coef.lasso1 != 0) # 11
unname(which(coef.lasso1 != 0))
# [1]   1   2   3   4   5   7   8   9  10  71 102
mean((y-predict.lasso1)^2) # 23.2942

# lasso 2. tumortype is categorical, intercept = FALSE
X <- cbind(x, model.matrix( ~ .-1, data.frame(factor(tumortype))))
dim(X) # 104 columns
set.seed(1234)
fit.lasso2 <- cv.glmnet(X, y, alpha=1, intercept = FALSE)
predict.lasso2 <- predict(fit.lasso2, newx=X, s="lambda.min", type = 'response')[,1]
coef.lasso2 <- coef(fit.lasso2)[,1]
length(coef.lasso2) # 105
sum(coef.lasso2 != 0) # 12
unname(which(coef.lasso2 != 0))
# [1]   2   3   4   5   7   8   9  10  71 103 104 105
mean((y-predict.lasso2)^2)  # 23.3353

# lasso 3. tumortype is categorical, intercept = TRUE
set.seed(1234)
fit.lasso3 <- cv.glmnet(X, y, alpha=1)
predict.lasso3 <- predict(fit.lasso3, newx=X, s="lambda.min", type = 'response')[,1]
coef.lasso3 <- coef(fit.lasso3)[,1]
length(coef.lasso3) # 105
sum(coef.lasso3 != 0) # 11
unname(which(coef.lasso3 != 0))
# [1]   1   2   3   4   5   7   8   9  10  71 102
mean((y-predict.lasso3)^2)  # 23.16397

# SGL
set.seed(1234)
index <- c(1:p, rep(p+1, nlevels(factor(tumortype))))
data <- list(x=X, y=y)
cvFit = cvSGL(data, index, type = "linear", alpha=.95) # this alpha is the default
                      # this takes a longer time
plot(cvFit)
i <- which.min(cvFit$lldiff); i # 15
Fit = SGL(data, index, type = "linear", lambdas = cvFit$lambdas)
sum(Fit$beta[, i] != 0) # 28
pred.SGL <- predictSGL(Fit, X, i)
mean((y-pred.SGL)^2) # 23.33841
which(Fit$beta[, i] != 0)
# [1]   1   2   3   4   6   7   8   9  10  12  21  23  29  35  37  40  45
# [18]  53  60  62  68  70  85  86 101 102 103 104

# Plot. A mess unless n is small
dat <- tibble(y=y, 
              glm=pred.glm, 
              lasso1=predict.lasso1,
              lasso2=predict.lasso2,
              SGL=pred.SGL) %>% 
          pivot_longer(-y, names_to="method", values_to="predict")
ggplot(dat, aes(x=y, y=predict, color=method)) + geom_point() + geom_abline(slope=1)
    • How to include all levels of a factor variable in a model matrix in R - model.matrix, Changing the column names for model.matrix output
    • How does glmnet's standardize argument handle dummy variables?

    Adaptive lasso and weights

    Oracle property and adaptive lasso

    • Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties, Fan & Li (2001) JASA
    • Adaptive Lasso: What it is and how to implement in R. Adaptive lasso weeks to minimize [math]\displaystyle{ RSS(\beta) + \lambda \sum_1^p \hat{\omega}_j |\beta_j| }[/math] where [math]\displaystyle{ \lambda }[/math] is the tuning parameter, [math]\displaystyle{ \hat{\omega}_j = \frac{1}{(|\hat{\beta}_j^{ini}|)^\gamma} }[/math] is the adaptive weights vector and [math]\displaystyle{ \hat{\beta}_j^{ini} }[/math] is an initial estimate of the coefficients obtained through ridge regression. Adaptive Lasso ends up penalizing more those coefficients with lower initial estimates. [math]\displaystyle{ \gamma }[/math] is a positive constant for adjustment of the adaptive weight vector, and the authors suggest the possible values of 0.5, 1 and 2.
    • When n goes to infinity, [math]\displaystyle{ \hat{\omega}_j |\beta_j| }[/math] converges to [math]\displaystyle{ I(\beta_j \neq 0) }[/math]. So the adaptive Lasso procedure can be regarded as an automatic implementation of best-subset selection in some asymptotic sense.
    • What is the oracle property of an estimator? An oracle estimator must be consistent in 1) variable selection and 2) consistent parameter estimation.
    • Oracle property: Oracle property is a name given to techniques for estimating the regression parameters in the models fitted to high-dimensional data which have the property that they can correctly select the nonzero coefficients with the probability converging to one and that the estimators of nonzero coefficients are asymptotically normal with the identical means and covariances that they would have if the zero coefficients were known in advance that is the estimators are asymptotically as efficient as the ideal estimation assisted by an 'oracle' who knows which coefficients are nonzero.
    • (Linear regression) The adaptive lasso and its oracle properties Zou (2006, JASA)
    • (Cox model) Adaptive-LASSO for Cox's proportional hazard model by Zhang and Lu (2007, Biometrika)
    • When the LASSO fails???. Adaptive lasso is used to demonstrate its usefulness.
    • On the use of cross-validation for the calibration of the adaptive lasso Ballout 2023

    Biologically weighted LASSO

    Biologically weighted LASSO: enhancing functional interpretability in gene expression data analysis 2024

    Survival data

    data(CoxExample)
dim(x) # 1000 x 30
ind.train <- 1:nrow(x)/2
cv.fit <- cv.glmnet(x[ind.train, ], y[ind.train, ], family="cox")
coef(cv.fit, s = "lambda.min") 
    # 30 x 1, coef(...) is equivalent to predict(type="coefficients",...)
pr <- predict(cv.fit, x[-ind.train, ], type = "link", s = "lambda.min")
    # the default option for type is 'link' which gives the linear predictors for "cox" models. 
pr2 <- x[-ind.train, ] %*% coef(cv.fit, s = "lambda.min")
all.equal(pr[, 1], pr2[, 1]) # [1] TRUE
class(pr) # [1] "matrix"
class(pr2) # [1] "dgeMatrix"
# we can also use predict() with glmnet object
pr22 <- predict(fit, x[-ind.train, ], type='link', s = cv.fit$lambda.min)
all.equal(pr[, 1], pr22[, 1]) # [1] TRUE

pr3 <- predict(cv.fit, x[-ind.train, ], type = "response", s = "lambda.min")
range(pr3)  # relative risk [1]  0.05310623 19.80143519

    Logistic

    Multi-response

    Survival analysis on rare events using group-regularized multi-response Cox regression Li et al 2021

    Weights on samples for unbalanced responses data for binary response

    w1 <- rep(1, n.sample)
w1[bin == "Sensitive" <- sum(bin == "Resistant") / sum(bin == "Sensitive")
cv.glmnet(xx, yy, family = 'binomial', weights = w1)

    Proportional matrix: family="binomial"

    What does a proportional matrix look like for glmnet response variable in R? You can provide a matrix of proportion, 2nd column for success but this assumes the weight or n is same for all observations:

    glmnet 4.0: family

    glmnet v4.0: generalizing the family parameter

    Timing

    nvec <- c(100, 400)
pvec <- c(1000, 5000)
for(n in nvec)
  for(p in pvec) {
    nzc = trunc(p/10)  # 1/10 variables are non-zeros 
    x = matrix(rnorm(n * p), n, p)
    beta = rnorm(nzc)
    fx = x[, seq(nzc)] %*% beta/3
    hx = exp(fx)
    ty = rexp(n, hx)
    tcens = rbinom(n = n, prob = 0.3, size = 1)  # censoring indicator
    y = cbind(time = ty, status = 1 - tcens)  # y=Surv(ty,1-tcens) with library(survival)
    foldid = sample(rep(seq(10), length = n))
    o <- system.time(fit1_cv <- cv.glmnet(x, y, family = "cox", foldid = foldid) )
    cat(sprintf("n=%1d, p=%5d, time=%8.3f\n", n, p, o['elapsed']))
}

    Running on core i7 2.6GHz, macbook pro 2018. Unit is seconds.

    p ∖ n 100 400
    1000 5 58
    5000 9 96

    Xeon E5-2680 v4 @ 2.40GHz

    p ∖ n 100 400
    1000 7 98
    5000 13 125

    All interactions

    How to make all interactions before using glmnet

    Algorithm

    warm start

    Soft thresholding

    • Finding the Right Balance: Better Choices with Lasso Regression
    • The Lasso penalization results in the following update for each coefficient:
      [math]\displaystyle{ \beta_j = \text{sign}(\tilde{\beta_j}) \cdot \max\left(0, |\tilde{\beta_j}| - \frac{\lambda}{2}\right) }[/math]
      where [math]\displaystyle{ \tilde{\beta_j} }[/math] represents the least-squares estimate without the penalty, and [math]\displaystyle{ \lambda }[/math] is the penalty term. This is the soft-thresholding operation.
      • For values of [math]\displaystyle{ |\tilde{\beta_j}| \leq \frac{\lambda}{2} }[/math], the soft-thresholding rule will set [math]\displaystyle{ \beta_j = 0 }[/math].
      • For values of [math]\displaystyle{ |\tilde{\beta_j}| \gt \frac{\lambda}{2} }[/math], the soft-thresholding rule shrinks the coefficients by a fixed amount [math]\displaystyle{ \lambda/2 }[/math], and retains the sign without setting them to zero.
    • The glmnet package uses a coordinate descent algorithm to optimize the Lasso objective function
      1. Initialization: Start with initial values for the coefficients, often set to zero.
      2. Coordinate-wise Updates: The algorithm applies the soft-thresholding formula to update [math]\displaystyle{ \beta_j }[/math] based on the current values of all other coefficients.
      3. Iteration: This process is repeated, updating one coefficient at a time while keeping the others fixed, iterating over all predictors in cycles until convergence is reached.
    • IEOR 265 – Lecture 6 Lasso Regression
    • Lecture 5: Soft-Thresholding and Lasso

    Gradient descent

    Cyclical coordinate descent algorithm

    Quadratic programming

    Other

    Simulation study

    Feature selection

    Release

    Discussion

    Prediction

    ROC

    How to plot ROC-curve for logistic regression (LASSO) in R?

    LASSO vs Least angle regression

    LassoNet

    R packages related to glmnet

    caret

    Caret

    Tidymodels and tune

    Tidymodels

    biglasso

    biglasso: Extend Lasso Model Fitting to Big Data in R

    snpnet

    snpnet: Efficient Lasso Solver for Large-scale SNP Data

    cornet: Elastic Net with Dichotomised Outcomes

    Pretraining

    Python

    GLMNet in Python: Generalized Linear Models

    Other methods, reviews

Retrieved from "https://wiki.taichimd.us/index.php?title=Glmnet&oldid=40660"