PCA

From 太極
Jump to navigation Jump to search

Principal component analysis

What is PCA

Linear Algebra

Linear Algebra for Data Science with examples in R

R source code

> stats:::prcomp.default
function (x, retx = TRUE, center = TRUE, scale. = FALSE, tol = NULL, 
    ...) 
{
    x <- as.matrix(x)
    x <- scale(x, center = center, scale = scale.)
    cen <- attr(x, "scaled:center")
    sc <- attr(x, "scaled:scale")
    if (any(sc == 0)) 
        stop("cannot rescale a constant/zero column to unit variance")
    s <- svd(x, nu = 0)
    s$d <- s$d/sqrt(max(1, nrow(x) - 1))
    if (!is.null(tol)) {
        rank <- sum(s$d > (s$d[1L] * tol))
        if (rank < ncol(x)) {
            s$v <- s$v[, 1L:rank, drop = FALSE]
            s$d <- s$d[1L:rank]
        }
    }
    dimnames(s$v) <- list(colnames(x), paste0("PC", seq_len(ncol(s$v))))
    r <- list(sdev = s$d, rotation = s$v, center = if (is.null(cen)) FALSE else cen, 
        scale = if (is.null(sc)) FALSE else sc)
    if (retx) 
        r$x <- x %*% s$v
    class(r) <- "prcomp"
    r
}
<bytecode: 0x000000003296c7d8>
<environment: namespace:stats>

rank of a matrix

Matrix::rankMatrix()

R example

Principal component analysis (PCA) in R including bi-plot.

R built-in plot

http://genomicsclass.github.io/book/pages/pca_svd.html 

pc <- prcomp(x)
group <- as.numeric(tab$Tissue)
plot(pc$x[, 1], pc$x[, 2], col = group, main = "PCA", xlab = "PC1", ylab = "PC2")

The meaning of colors can be found by palette().

  1. black
  2. red
  3. green3
  4. blue
  5. cyan
  6. magenta
  7. yellow
  8. gray

palmerpenguins data

PCA with penguins and recipes

Theory with an example

Principal Component Analysis in R: prcomp vs princomp

Biplot

factoextra

Properties

  • Definition. If x is a random vector with mean [math]\displaystyle{ \mu }[/math] and covariance matrix [math]\displaystyle{ \Sigma }[/math], the the principal component transformation is
    [math]\displaystyle{ y = \Gamma ' (x - \mu), }[/math]
    where [math]\displaystyle{ \Gamma }[/math] is orthogonal, [math]\displaystyle{ \Gamma' \Sigma \Gamma = \Lambda }[/math] is diagonal and [math]\displaystyle{ \lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_p \geq 0 }[/math]. The strict positivity of the eigenvalues [math]\displaystyle{ \lambda_i }[/math] is guaranteed if [math]\displaystyle{ \Sigma }[/math] is positive definite. The ith principal component of x may be defined as the ith element of the vector y, namely, as [math]\displaystyle{ y_i = \gamma_{(i)}' (x-\mu) }[/math]. Here [math]\displaystyle{ \gamma_{(i)} }[/math] is the ith column of [math]\displaystyle{ \Gamma }[/math], and may be called the ith vector of principal component loadings.
  • Properties
    • [math]\displaystyle{ E(y_i) =0, }[/math]
    • [math]\displaystyle{ Var(y_i) =\lambda_i, }[/math]
    • [math]\displaystyle{ Cov(y_i, y_j) =0, i \neq j, }[/math]
    • [math]\displaystyle{ Var(y_1) \geq Var(y_2) \geq \cdots Var(y_p) \geq 0, }[/math]
    • [math]\displaystyle{ \sum Var(y_i) = tr \Sigma, }[/math] total variation
    • [math]\displaystyle{ \prod Var(y_i) = |\Sigma| }[/math].
  • The sum of the first k eigenvalues divided by the sum of all the eigenvalues, [math]\displaystyle{ (\lambda_1 + \cdots + \lambda_k)/(\lambda_1 + \cdots + \lambda_p) }[/math], represents the proportion of total variation explained by the first k principal components.
  • The principal component of a random vector are not scale-invariant. For example, given three variables, say weight in pounds, height in feet, and age in years, we may seek a principal component expressed say in ounces, inches, and decades. Two procedures see feasible:
    • Multiple the data by 16, 12 and .1, respectively, and then carry out a PCA,
    • Carry out a PCA and then multiply the elements of the relevant component by 16, 12 and .1.
    Unfortunately the above procedures do not generally lead to the same result
  • Number of principals?
    • Include just enough components to explain say 90% of the total variations scree graph;
    • Exclude those principal components whose eigenvalues are less than the average (Kaiser)
  • Rotation/loadings matrix is orthogonal 
    x <- matrix(c(10,6,12,5,11,4,9,7,8,5,10,6,3,3,2.5,2,2,2.8,1.3,4,1,1,2,7), 
     nr=4)
x <- t(x)  # 6 samples, 4 genes
rownames(x) <- paste("mouse",1:6)
colnames(x) <- paste("gene", 1:4)
pr <- prcomp(x, scale = T)

t(pr$rotation) %*% pr$rotation - diag(4)
#               PC1           PC2           PC3           PC4
# PC1  0.000000e+00  0.000000e+00  1.804112e-16 -2.081668e-17
# PC2  0.000000e+00 -1.110223e-16  1.387779e-16 -2.220446e-16
# PC3  1.804112e-16  1.387779e-16 -2.220446e-16 -5.551115e-17
# PC4 -2.081668e-17 -2.220446e-16 -5.551115e-17  6.661338e-16
range(t(pr$rotation) %*% pr$rotation - diag(4))
# [1] -2.220446e-16  6.661338e-16

range(pr$rotation %*% t(pr$rotation) - diag(4))
[1] -6.661338e-16  2.220446e-16
  • Principals are orthogonal 
    cor(pr$x) |> round(3)
#     PC1 PC2 PC3 PC4
# PC1   1   0   0   0
# PC2   0   1   0   0
# PC3   0   0   1   0
# PC4   0   0   0   1
  • SLC (standardized linear combination). A linear combination [math]\displaystyle{ l' x }[/math] is SLC if [math]\displaystyle{ \sum l_i^2 = 1 }[/math]. 
    apply(pr$rotation, 2, function(x) sum(x^2))
# PC1 PC2 PC3 PC4 
#   1   1   1   1
  • No SLC of x has a variance larger than [math]\displaystyle{ \lambda_1 }[/math], the variance of the first principal component.
  • If [math]\displaystyle{ \alpha = a'x }[/math] is a SLC of x which is uncorrelated with the first k principal component of x, then the variance of [math]\displaystyle{ \alpha }[/math] is maximized when [math]\displaystyle{ \alpha }[/math] is the (k+1)th principal component of x.

Tips

Removing Zero Variance Columns

Efficiently Removing Zero Variance Columns (An Introduction to Benchmarking) 

# Assume df is a data frame or a list (matrix is not enough!)
removeZeroVar3 <- function(df){
  df[, !sapply(df, function(x) min(x) == max(x))]
}
# Assume df is a matrix
removeZeroVar3 <- function(df){
  df[, !apply(df, 2, function(x) min(x) == max(x))]
}

# benchmark
dim(t(tpmlog))  # [1]    58 28109
system.time({a <- t(tpmlog); a <- a[, apply(a, 2, sd) !=0]}) # 0.54
system.time({a <- t(tpmlog); a <- removeZeroVar3(a)})        # 0.18

Removal of constant columns in R

Do not scale your matrix

https://privefl.github.io/blog/(Linear-Algebra)-Do-not-scale-your-matrix/

Apply the transformation on test data

Calculated by Hand

http://strata.uga.edu/software/pdf/pcaTutorial.pdf

Variance explained by the first XX components

  • StatQuest: Principal Component Analysis (PCA), Step-by-Step. So the variance explained by the K-th principals means (pr$sdev^2)[k]/sum(pr$sdev^2). 
    x <- matrix(c(10,6,12,5,11,4,9,7,8,5,10,6,3,3,2.5,2,2,2.8,1.3,4,1,1,2,7), nr=4)
x <- t(x)  # 6 samples, 4 genes
rownames(x) <- paste("mouse",1:6)
colnames(x) <- paste("gene", 1:4)
pr <- prcomp(x, scale = T)

names(pr)
# [1] "sdev"     "rotation" "center"   "scale"    "x"

summary(pr)
# Importance of components:
#   PC1    PC2     PC3     PC4
# Standard deviation     1.6966 1.0091 0.29225 0.13321
# Proportion of Variance 0.7197 0.2546 0.02135 0.00444
# Cumulative Proportion  0.7197 0.9742 0.99556 1.00000
apply(x, 2, var)|> sum()
# [1] 48.10667
apply(pr$x, 2, var) |> sum()
# [1] 4

cumsum(pr$sdev^2)
# [1] 2.878596 3.896846 3.982256 4.000000
cumsum(pr$sdev^2)/sum(pr$sdev^2)
# [1] 0.7196489 0.9742115 0.9955639 1.0000000
round(pr$sdev^2/sum(pr$sdev^2), 4)
# [1] 0.7196 0.2546 0.0214 0.0044

pr$x  # n x p
#               PC1         PC2         PC3         PC4
# mouse 1 -1.968265 -0.58969012  0.19246648 -0.04876951
# mouse 2 -1.350451  0.80465212 -0.48923602  0.04034721
# mouse 3 -1.268878  0.09892713  0.28501094  0.01538360
# mouse 4  1.368867 -1.36891596 -0.20417800 -0.13328931
# mouse 5  1.484377 -0.38237471  0.06095533  0.23453002
# mouse 6  1.734349  1.43740154  0.15498128 -0.10820202

pr$rotation
#               PC1         PC2        PC3        PC4
# gene 1 -0.5723917  0.01405298 -0.8132373  0.1039973
# gene 2 -0.5327490 -0.39598718  0.4450008  0.6011214
# gene 3 -0.5839377  0.00459261  0.3154255 -0.7479990
# gene 4 -0.2180896  0.91813701  0.2027959  0.2614100

pr$center
#   gene 1   gene 2   gene 3   gene 4 
# 5.833333 3.633333 6.133333 5.166667 

pr$scale
#   gene 1   gene 2   gene 3   gene 4 
# 4.355074 1.768238 4.716637 1.940790 

scale(x) %*% pr$rotation
#               PC1         PC2         PC3         PC4
# mouse 1 -1.968265 -0.58969012  0.19246648 -0.04876951
# mouse 2 -1.350451  0.80465212 -0.48923602  0.04034721
# mouse 3 -1.268878  0.09892713  0.28501094  0.01538360
# mouse 4  1.368867 -1.36891596 -0.20417800 -0.13328931
# mouse 5  1.484377 -0.38237471  0.06095533  0.23453002
# mouse 6  1.734349  1.43740154  0.15498128 -0.10820202
  • Singular Value Decomposition (SVD) Tutorial Using Examples in R 
    svd2 <- svd(Z)
variance.explained <- prop.table(svd2$d^2)

    OR 

    pr <- prcomp(USArrests, scale. = TRUE) # PS default is scale. = FALSE
summary(pr)
# Importance of components:
#                           PC1    PC2     PC3     PC4
# Standard deviation     1.5749 0.9949 0.59713 0.41645
# Proportion of Variance 0.6201 0.2474 0.08914 0.04336  <-------
# Cumulative Proportion  0.6201 0.8675 0.95664 1.00000
pr$sdev^2/ sum(pr$sdev^2) 
# [1] 0.62006039 0.24744129 0.08914080 0.04335752

Visualization

  • Tutorial:Basic normalization, batch correction and visualization of RNA-seq data. log(CPM) was used.
  • DESeq2 - PCAplot differs between rlog and vsd transformation. VST is the one to use or log2(count + 1), which can be performed with normTransform().
  • ggfortify or the basic method Pca autoplot.png Pca directly2.png Pca factoextra.png Pca ggplot2.png
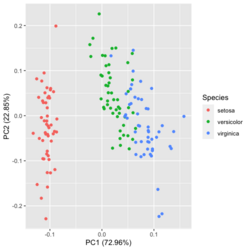
    ?ggfortify::autoplot.prcomp 
    library(ggfortify)
iris[1:2,]
#   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
# 1          5.1         3.5          1.4         0.2  setosa
# 2          4.9         3.0          1.4         0.2  setosa
df <- iris[1:4]  # exclude "Species" column

pca_res <- prcomp(df, scale. = TRUE)
p <- autoplot(pca_res, data = iris, colour = 'Species')
# OR turn off scaling on axes in order to get the same plot as the direct method
# p <- autoplot(pca_res, data = iris, colour = 'Species', scale = 0) 
p  # PC1 (72.96%), PC2 (22.85%)

library(plotly)
ggplotly(p)

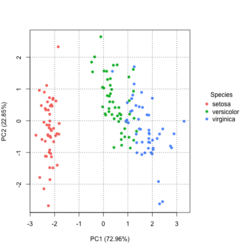
    Basic method 

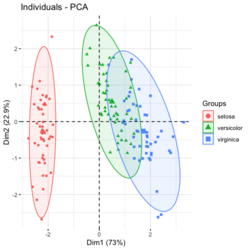
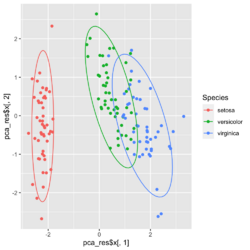
    group <- as.numeric(iris$Species)

# ggplot2's palette
gg_color_hue <- function(n) {
  hues = seq(15, 375, length = n + 1)
  hcl(h = hues, l = 65, c = 100)[1:n]
}
n <- 3   # iris$Species has 3 levels
cols = gg_color_hue(n)

prp <- pca_res$sdev^2/ sum(pca_res$sdev^2) 
xlab <- paste0("PC1 (", round(prp[1]*100,2), "%)")
ylab <- paste0("PC2 (", round(prp[2]*100,2), "%)")
omar <- par(mar=c(5,4,4,8))
plot(pca_res$x[, 1], pca_res$x[, 2], 
     xlab = xlab, ylab = ylab,
     col = cols[group], pch=16)
grid(NULL, NULL, lty=3, lwd=1, col="#000000")
par(xpd=TRUE)
legend(4, 1, legend = levels(iris$Species), col=cols, pch=16, bty = "n", title = "Species")
par(xpd=FALSE)
par(omar)

    ? factoextra::fviz_pca_ind 

    library(factoextra)
fviz_pca_ind(pca_res, 
             habillage=iris$Species,
             label = "none",
             ellipse.level=0.95,  # default
             addEllipses=TRUE, title = "PCA")
  • Why the ellipses generated by fviz_pca_ind() and stat_ellipse() are different? How does R calculate the PCA ellipses? 
    # Example dataset
data <- iris

# ggplot2 method
ggplot(data, aes(x = Sepal.Length, y = Sepal.Width)) +
     geom_point() +
     stat_ellipse(level = 0.95, type = "norm") + 
     ggtitle("norm distribution")

# Base R method
# Select x and y variables
x <- data$Sepal.Length
y <- data$Sepal.Width

# Calculate the mean of x and y
mean_x <- mean(x)
mean_y <- mean(y)

# Create a covariance matrix
cov_matrix <- cov(cbind(x, y))

# Calculate the eigenvalues and eigenvectors of the covariance matrix
eigen_decomp <- eigen(cov_matrix)
eig_val <- eigen_decomp$values
eig_vec <- eigen_decomp$vectors

# Set the confidence level
confidence_level <- 0.95

# Get the number of observations
n <- length(x)

# Compute the scaling factor
t_val <- sqrt(2 * qf(confidence_level, 2, n - 1))

# Generate points for the ellipse
theta <- seq(0, 2 * pi, length.out = 100)
ellipse_coords <- t(eig_vec %*% diag(sqrt(eig_val)) %*% rbind(cos(theta), sin(theta))) * t_val

# Translate the ellipse to the mean
ellipse_coords[,1] <- ellipse_coords[,1] + mean_x
ellipse_coords[,2] <- ellipse_coords[,2] + mean_y

# Plot the points and the ellipse
plot(x, y, xlab = "Sepal Length", ylab = "Sepal Width", main = "Scatter Plot with Confidence Ellipse")
lines(ellipse_coords, col = "red", lwd = 2)
  • Two categorical variables: one point shape and one fill color?
  • PCA and Visualization
  • Scree plots from the FactoMineR package (based on ggplot2)
  • 2 lines of code, plotPCA() from DESeq2

Interactive Principal Component Analysis

center and scale

What does it do if we choose center=FALSE in prcomp()?

In USArrests data, use center=FALSE gives a better scatter plot of the first 2 PCA components. 

x1 = prcomp(USArrests) 
x2 = prcomp(USArrests, center=F)
plot(x1$x[,1], x1$x[,2])  # looks random
windows(); plot(x2$x[,1], x2$x[,2]) # looks good in some sense

"scale. = TRUE" and Mean subtraction

  • PCA is sensitive to the scaling of the variables. See PCA -> Further considerations.
  • https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/prcomp
  • By default scale. = FALSE in prcomp()
  • By default, it centers the variable to have mean equals to zero. With parameter scale. = T, we normalize the variables to have standard deviation equals to 1. See also Normalizing all the variarbles vs. using scale=TRUE option in prcomp in R.
  • Practical Guide to Principal Component Analysis (PCA) in R & Python
  • What is the best way to scale parameters before running a Principal Component Analysis (PCA)?
    • As a rule of thumb, if all your variables are measured on the same scale and have the same unit, it might be a good idea *not* to scale the variables (i.e., PCA based on the covariance matrix). If you want to maximize variation, it is fair to let variables with more variation contribute more. On the other hand, If you have different types of variables with different units, it is probably wise to scale the data first (i.e., PCA based on the correlation matrix).
    • If all your variables are recorded in the same scale and/or the difference in variable magnitudes are of interest, you may choose not to normalize your data prior to PCA. See Normalizing all the variarbles vs. using scale=TRUE option in prcomp in R
  • Let's compare the difference using the USArrests data 
    USArrests[1:3,]
#         Murder Assault UrbanPop Rape
# Alabama   13.2     236       58 21.2
# Alaska    10.0     263       48 44.5
# Arizona    8.1     294       80 31.0

pca1 <- prcomp(USArrests)  # inappropriate, default is scale. = FALSE
pca2 <- prcomp(USArrests, scale. = TRUE)
pca1$x[1:3, 1:3]
#               PC1        PC2       PC3
# Alabama  64.80216 -11.448007 -2.494933
# Alaska   92.82745 -17.982943 20.126575
# Arizona 124.06822   8.830403 -1.687448
pca2$x[1:3, 1:3]
#                PC1        PC2         PC3
# Alabama -0.9756604  1.1220012 -0.43980366
# Alaska  -1.9305379  1.0624269  2.01950027
# Arizona -1.7454429 -0.7384595  0.05423025

set.seed(1)
X <- matrix(rnorm(10*100), nr=10)
pca1 <- prcomp(X)
pca2 <- prcomp(X, scale. = TRUE)
range(abs(pca1$x - pca2$x))  # [1] 3.764350e-16 1.139182e+01
par(mfrow=c(1,2))
plot(pca1$x[,1], pca1$x[, 2], main='scale=F')
plot(pca2$x[,1], pca2$x[, 2], main='scale=T')
par(mfrow=c(1,1))
# rotation matrices are different
# sdev are different
# rotation matrices are different

# Same observations for a long matrix too
set.seed(1)
X <- matrix(rnorm(10*100), nr=100)
pca1 <- prcomp(X)
pca2 <- prcomp(X, scale. = TRUE)
range(abs(pca1$x - pca2$x))  # [1] 0.001915974 5.112158589

svd1 <- svd(USArrests)
svd2 <- svd(scale(USArrests, F, T))
svd1$d
# [1] 1419.06140  194.82585   45.66134   18.06956
svd2$d
# [1] 13.560545  2.736843  1.684743  1.335272
# u (or v) are also different
  • Biplot

Number of components

Obtaining the number of components from cross validation of principal components regression

AIC/BIC in estimating the number of components

Consistency of AIC and BIC in estimating the number of significant components in high-dimensional principal component analysis

PCA and SVD

Using the SVD to perform PCA makes much better sense numerically than forming the covariance matrix to begin with, since the formation of [math]\displaystyle{ X X^T }[/math] can cause loss of precision.

R example

covMat <- matrix(c(4, 0, 0, 1), nr=2)
p <- 2
n <- 1000
set.seed(1)
x <- mvtnorm::rmvnorm(n, rep(0, p), covMat)
svdx <- svd(x)
result= prcomp(x, scale = TRUE) 
summary(result)
# Importance of components:
#                          PC1    PC2
# Standard deviation     1.0004 0.9996
# Proportion of Variance 0.5004 0.4996
# Cumulative Proportion  0.5004 1.0000

# It seems scale = FALSE result can reflect the original data
result2 <- prcomp(x, scale = FALSE) # DEFAULT
summary(result2)
# Importance of components:
#                           PC1    PC2
# Standard deviation     2.1332 1.0065  ==> Close to the original data
                                     #  ==> How to compute
                              # sqrt(eigen(var(x))$values ) = 2.133203 1.006460
# Proportion of Variance 0.8179 0.1821  ==> How to verify
                                        # 2.1332^2/(2.1332^2+1.0065^2) = 0.8179
# Cumulative Proportion  0.8179 1.0000
result2$sdev
# 2.133203 1.006460    #  sqrt( SS(distance)/(n-1) )
result2$sdev^2 / sum(result2$sdev^2)
# 0.8179279 0.1820721
result2$rotation
#                PC1           PC2
# [1,]  0.9999998857 -0.0004780211
# [2,] -0.0004780211 -0.9999998857
result2$sdev^2 * (n-1)
# [1] 4546.004 1011.948   #  SS(distance)

# eigenvalue for PC1 = singular value^2
svd(scale(x, center=T, scale=F))$d
# [1] 67.42406 31.81113
svd(scale(x, center=T, scale=F))$d ^ 2  # SS(distance)
# [1] 4546.004 1011.948
svd(scale(x, center=T, scale=F))$d / sqrt(nrow(x) -1)
# [1] 2.133203 1.006460     ==> This is the same as prcomp()$sdev
svd(scale(x, center=F, scale=F))$d / sqrt(nrow(x) -1)
# [1] 2.135166 1.006617     ==> So it does not matter to center or scale
svd(var(x))$d
# [1] 4.550554 1.012961
svd(scale(x, center=T, scale=F))$v # same as result2$rotation
#               [,1]          [,2]
# [1,]  0.9999998857 -0.0004780211
# [2,] -0.0004780211 -0.9999998857
sqrt(eigen(var(x))$values )
# [1] 2.133203 1.006460
eigen(t(scale(x,T,F)) %*% scale(x,T,F))$values  # SS(distance)
# [1] 4546.004 1011.948
sqrt(eigen(t(scale(x,T,F)) %*% scale(x,T,F))$values ) # Same as svd(scale(x.T,F))$d
# [1] 67.42406 31.81113.   

# So SS(distance) = eigen(t(scale(x,T,F)) %*% scale(x,T,F))$values
#                 = svd(scale(x.T,F))$d ^ 2

Related to Factor Analysis

In short,

  1. In Principal Components Analysis, the components are calculated as linear combinations of the original variables. In Factor Analysis, the original variables are defined as linear combinations of the factors.
  2. In Principal Components Analysis, the goal is to explain as much of the total variance in the variables as possible. The goal in Factor Analysis is to explain the covariances or correlations between the variables.
  3. Use Principal Components Analysis to reduce the data into a smaller number of components. Use Factor Analysis to understand what constructs underlie the data.

prcomp vs princomp

prcomp vs princomp from sthda. prcomp() is preferred compared to princomp().

Missing data

pcaMethods

Relation to Multidimensional scaling/MDS

With no missing data, classical MDS (Euclidean distance metric) is the same as PCA.

Comparisons are here.

Differences are asked/answered on stackexchange.com. The post also answered the question when these two are the same.

isoMDS (Non-metric)

cmdscale (Metric)

Matrix factorization methods

http://joelcadwell.blogspot.com/2015/08/matrix-factorization-comes-in-many.html Review of principal component analysis (PCA), K-means clustering, nonnegative matrix factorization (NMF) and archetypal analysis (AA).

Outlier samples

Detecting outlier samples in PCA

Reconstructing images

Reconstructing images using PCA

Sparse PCA

Misc

Data reduction prior to inference: Are there consequences of comparing groups using a t‐test based on principal component scores? Bedrick 2019

PCA for Categorical Variables

psych package

Principal component analysis (PCA) in R

glmpca: Generalized PCA for dimension reduction of sparse counts

Feature selection and dimension reduction for single-cell RNA-Seq based on a multinomial model

Retrieved from "https://wiki.taichimd.us/index.php?title=PCA&oldid=40162"