Heatmap
Clustering
Task View
https://cran.r-project.org/web/views/Cluster.html
k-means clustering
- Assumptions, a post from varianceexplained.org.
- UTILIZING K-MEANS TO EXTRACT COLOURS FROM YOUR FAVOURITE IMAGES
- k-Means 101: An introductory guide to k-Means clustering in R. Interactive 3D plot. Elbow plot.
k-medoids/Partitioning Around Medoids (PAM)
- https://en.wikipedia.org/wiki/K-medoids
- https://www.rdocumentation.org/packages/cluster/versions/2.0.7-1/topics/pam
Number of clusters: Intraclass Correlation/ Intra Cluster Correlation (ICC)
- https://en.wikipedia.org/wiki/Intraclass_correlation
- ICC was used by Integrating gene expression and GO classification for PCA by preclustering by Hann et al 2010
mbkmeans
- https://bioconductor.org/packages/release/bioc/html/mbkmeans.html Proposed by Sculley 2010. Useful for scRNA-Seq data. talk by Hicks 2021.
Hierarchical clustering
For the kth cluster, define the Error Sum of Squares as [math]\displaystyle{ ESS_m = }[/math] sum of squared deviations (squared Euclidean distance) from the cluster centroid. [math]\displaystyle{ ESS_m = \sum_{l=1}^{n_m}\sum_{k=1}^p (x_{ml,k} - \bar{x}_{m,k})^2 }[/math] in which [math]\displaystyle{ \bar{x}_{m,k} = (1/n_m) \sum_{l=1}^{n_m} x_{ml,k} }[/math] the mean of the mth cluster for the k-th variable, [math]\displaystyle{ x_{ml,k} }[/math] being the score on the kth variable [math]\displaystyle{ (k=1,\dots,p) }[/math] for the l-th object [math]\displaystyle{ (l=1,\dots,n_m) }[/math] in the mth cluster [math]\displaystyle{ (m=1,\dots,g) }[/math].
If there are C clusters, define the Total Error Sum of Squares as Sum of Squares as [math]\displaystyle{ ESS = \sum_m ESS_m, m=1,\dots,C }[/math]
Consider the union of every possible pair of clusters.
Combine the 2 clusters whose combination combination results in the smallest increase in ESS.
Comments:
- The default linkage is "complete" in R.
- Ward's method tends to join clusters with a small number of observations, and it is strongly biased toward producing clusters with the same shape and with roughly the same number of observations.
- It is also very sensitive to outliers. See Milligan (1980).
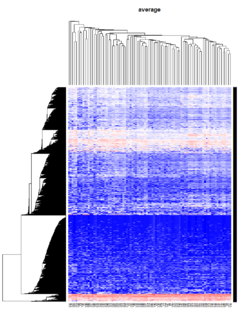
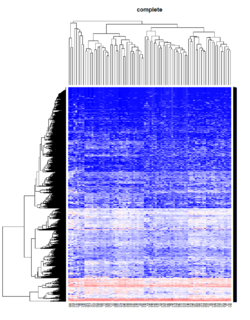
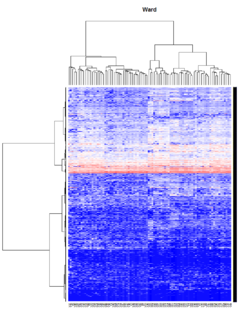
Take pomeroy data (7129 x 90) for an example:
library(gplots)
lr = read.table("C:/ArrayTools/Sample datasets/Pomeroy/Pomeroy -Project/NORMALIZEDLOGINTENSITY.txt")
lr = as.matrix(lr)
method = "average" # method <- "complete"; method <- "ward.D"; method <- "ward.D2"
hclust1 <- function(x) hclust(x, method= method)
heatmap.2(lr, col=bluered(75), hclustfun = hclust1, distfun = dist,
density.info="density", scale = "none",
key=FALSE, symkey=FALSE, trace="none",
main = method)
It seems average method will create a waterfall like dendrogram. Ward method will produce a tight clusters. Complete linkage produces a more 中庸 result.
Wards agglomeration/linkage method
- Ward's minimum variance method
- Murtagh, F., & Legendre, P. (2014). http://adn.biol.umontreal.ca/~numericalecology/Reprints/Murtagh_Legendre_J_Class_2014.pdf Ward’s hierarchical agglomerative clustering method: which algorithms implement Ward’s criterion?. Journal of Classification, 31(3), 274-295.
- IAML19.5 Single-link, complete-link, Ward's method. For Ward's method, we compute the centroid of the merged data. We calculate the deviations from each observations to the centroid and take the sum of this squared deviation.
- It is based on the notion that clusters of multivariate observations should be approximately elliptical in shape. We assume that the data from each of the clusters have been realized in a multivariate distribution. Therefore, it would follow that they would fall into an elliptical shape when plotted in a p-dimensional scatter plot. Basically, it looks at cluster analysis as an analysis of variance problem, instead of using distance metrics or measures of association.
- Agglomertive Hierarchical Clustering using Ward Linkage. We merge two clusters if they have the smallest merging cost/the sum of squares will increase when we merge them.
- Ward’s Hierarchical Agglomerative Clustering Method: Which Algorithms Implement Ward’s Criterion?. In R, only "ward.D2" minimizes the Ward clustering criterion and produces the Ward method.
- A Comparison of Hierarchical Methods for Clustering Functional Data Ferreira & Hitchcock 2009. Rand index. Ward’s method was usually the best, while average linkage performed best in some special situations, in particular, when the number of clusters is over specified (page 5 of the PDF).
- Comparison of hierarchical cluster analysis methods by cophenetic correlation 2013
- Since Ward method is used as the linkage method, the height is not limited to the original scale and can be larger than 2 if 1-Pearson distance is used. See the formula of the distance [math]\displaystyle{ d_{(ij)k} }[/math] in wikipedia page.
Density based clustering
http://www.r-exercises.com/2017/06/10/density-based-clustering-exercises/
Optimal number of clusters
- Cluster analysis -> Evaluation and assessment
- Determining the number of clusters in a data set
- https://datascienceplus.com/finding-optimal-number-of-clusters/
- 10 Tips for Choosing the Optimal Number of Clusters
- Determining Optimal Clusters
- Elbow method
- Silhouette method
- Gap statistic
- 10 Tips for Choosing the Optimal Number of Clusters
- Christian Hennig - Assessing the quality of a clustering
Silhouette score/width
- https://en.wikipedia.org/wiki/Silhouette_(clustering)
- Silhouettes: A graphical aid to the interpretation and validation of cluster analysis Rousseeuw 1987
- This silhouette shows which objects lie well within their cluster, and which ones are merely somewhere in between clusters.
- The entire clustering is displayed by combining the silhouettes into a single plot, allowing an appreciation of the relative quality of the clusters and an overview of the data configuration.
- The average silhouette width provides an evaluation of clustering validity, and might be used to select an ‘appropriate’ number of clusters. The k (number of clusters) that maximizes the average silhouette scores is the best k.
- https://github.com/cran/cluster/blob/master/R/silhouette.R
- Cluster Analysis 5th Edition. Everitt et al. page 129. Average silhouette width - the average of the s(i) over the entire data set – can be maximized to provide a more formal criterion for selecting the number of groups.
- The silhouette coefficient tells you how similar is a data point to the points in its own cluster compared to points in other clusters.
- Now the absolute value of the silhouette coefficient does not matter.
- Silhouette Coefficient (python)
- Silhouette Score = (b-a)/max(a,b) where
- a= average intra-cluster distance
- b= (minimum) average inter-cluster distance
- Clustering Validation Statistics: 4 Vital Things Everyone Should Know - Unsupervised Machine Learning
- Observations with a large Si (almost 1) are very well clustered
- A small Si (around 0) means that the observation lies between two clusters
- Observations with a negative Si are probably placed in the wrong cluster.
- Clustering Analysis in R using K-means
- Cluster silhouette plot
- Average silhouette width (one value for the whole data)
- Cluster evaluation
- Selecting the (optimal) number of clusters with silhouette analysis on KMeans clustering (python, scikit). Graphically compare silhouette width for different number of clusters.
- 10 Tips for Choosing the Optimal Number of Clusters
- Silhouette Analysis in K-means Clustering
- KMeans Silhouette Score Explained With Python Example
- Using Silhouette analysis for selecting the number of cluster for K-means clustering.
- Silhouette Method — Better than Elbow Method to find Optimal Clusters
- Selecting optimal number of clusters in KMeans Algorithm (Silhouette Score)
- When ai << bi, Si will be close to 1. This happens when a(i) is very close to its assigned cluster. A large value of bi implies its extremely far from its next closest cluster.
- Mean Silhouette score
- Average SS vs K plot from the ebook 'An R Companion for Introduction to Data Mining'. The ruspini data (originally used by Rousseeuw 1987) is used in the chapter.
- Silhouette width using generalized mean—A flexible method for assessing clustering efficiency Lengyel 2019
- clusterability: quantifies how well two different types of cells are separated from each other
kBET: k-nearest neighbour batch effect test
- Buttner, M., Miao, Z., Wolf, F. A., Teichmann, S. A. & Theis, F. J. A test metric for assessing single-cell RNA-seq batch correction. Nat. Methods 16, 43–49 (2019).
- https://github.com/theislab/kBET
- quantify mixability; how well cells of the same type from different batches were grouped together
Alignment score
- Butler, A., Hoffman, P., Smibert, P., Papalexi, E. & Satija, R. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 36, 411–420 (2018).
- quantify mixability; how well cells of the same type from different batches were grouped together
Compare 2 clustering methods, ARI
- https://en.wikipedia.org/wiki/Rand_index
- The Adjusted Rand index
- mclust::adjustedRandIndex()
- clue: package - Cluster Ensembles
- Examples: Effects of normalization on clustering from Normalization by distributional resampling of high throughput single-cell RNA-sequencing data Brown 2021.
Benchmark clustering algorithms
Using clusterlab to benchmark clustering algorithms
Louvain algorithm: graph-based method
Mahalanobis distance
- The Mahalanobis distance is a measure of the distance between a point P and a distribution D.
- Mahalanobis distance is widely used in cluster analysis and classification techniques.
- Mahalanobis distance can be used to classify a test point as belonging to one of N classes
- Mahalanobis distance and leverage are often used to detect outliers, especially in the development of linear regression models.
- How to Calculate Mahalanobis Distance in R. We can determine if any of the distances are statistically significant by calculating their p-values. The p-value for each distance is calculated as the p-value that corresponds to the Chi-Square statistic of the Mahalanobis distance with k-1 degrees of freedom, where k = number of variables. ?stats::mahalanobis
- Question: low-rank covariance case (high-dimensional data)? Matrix::rankMatrix(var(X)) < nr if nr=nrow(X) < nc=ncol(X).
- Mahalanobis distance: What if S is not invertible? Moore-Penrose generalized inverse/pseudo-inverse is used.
- To calculate mahalanobis distance when the number of observations are less than the dimension.
- What is the best distance measure for high dimensional data?
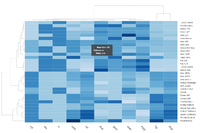
You probably don't understand heatmaps
- http://www.opiniomics.org/you-probably-dont-understand-heatmaps/
- Effect of number of genes
Evaluate the effect of centering & scaling
Different distance measures
9 Distance Measures in Data Science
1-correlation distance
Effect of centering and scaling on clustering of genes and samples in terms of distance. 'Yes' means the distance was changed compared to the baseline where no centering or scaling was applied.
| clustering genes | clustering samples | |
|---|---|---|
| centering on each genes | No | Yes* |
| scaling on each genes | No | Yes* |
- Note: Cor(X, Y) = Cor(X + constant scalar, Y). If the constant is not a scalar, the equation won't hold. Or think about plotting data in a 2 dimension space. If the X data has a constant shift for all observations/genes, then the linear correlation won't be changed.
Euclidean distance
| clustering genes | clustering samples | |
|---|---|---|
| centering on each genes | Yes | No1 |
| scaling on each genes | Yes | Yes2 |
Note
- [math]\displaystyle{ \sum(X_i - Y_i)^2 = \sum(X_i-c_i - (Y_i-c_i))^2 }[/math]
- [math]\displaystyle{ \sum(X_i - Y_i)^2 \neq \sum(X_i/c_i - Y_i/c_i)^2 }[/math]
Supporting R code
1. 1-Corr distance
source("http://www.bioconductor.org/biocLite.R")
biocLite("limma"); biocLite("ALL")
library(limma); library(ALL)
data(ALL)
eset <- ALL[, ALL$mol.biol %in% c("BCR/ABL", "ALL1/AF4")]
f <- factor(as.character(eset$mol.biol))
design <- model.matrix(~f)
fit <- eBayes(lmFit(eset,design))
selected <- p.adjust(fit$p.value[, 2]) < 0.05
esetSel <- eset [selected, ] # 165 x 47
heatmap(exprs(esetSel))
esetSel2 <- esetSel[sample(1:nrow(esetSel), 20), sample(1:ncol(esetSel), 10)] # 20 x 10
dist.no <- 1-cor(t(as.matrix(esetSel2)))
dist.mean <- 1-cor(t(sweep(as.matrix(esetSel2), 1L, rowMeans(as.matrix(esetSel2))))) # gene variance has not changed!
dist.median <- 1-cor(t(sweep(as.matrix(esetSel2), 1L, apply(esetSel2, 1, median))))
range(dist.no - dist.mean) # [1] -1.110223e-16 0.000000e+00
range(dist.no - dist.median) # [1] -1.110223e-16 0.000000e+00
range(dist.mean - dist.median) # [1] 0 0
So centering (no matter which measure: mean, median, ...) genes won't affect 1-corr distance of genes.
dist.mean <- 1-cor(t(sweep(as.matrix(esetSel2), 1L, rowMeans(as.matrix(esetSel2)), "/"))) dist.median <- 1-cor(t(sweep(as.matrix(esetSel2), 1L, apply(esetSel2, 1, median), "/"))) range(dist.no - dist.mean) # [1] -8.881784e-16 6.661338e-16 range(dist.no - dist.median) # [1] -6.661338e-16 6.661338e-16 range(dist.mean - dist.median) # [1] -1.110223e-15 1.554312e-15
So scaling after centering (no matter what measures: mean, median,...) won't affect 1-corr distance of genes.
How about centering / scaling genes on array clustering?
dist.no <- 1-cor(as.matrix(esetSel2)) dist.mean <- 1-cor(sweep(as.matrix(esetSel2), 1L, rowMeans(as.matrix(esetSel2)))) # array variance has changed! dist.median <- 1-cor(sweep(as.matrix(esetSel2), 1L, apply(esetSel2, 1, median))) range(dist.no - dist.mean) # [1] -1.547086 0.000000 range(dist.no - dist.median) # [1] -1.483427 0.000000 range(dist.mean - dist.median) # [1] -0.5283601 0.6164602 dist.mean <- 1-cor(sweep(as.matrix(esetSel2), 1L, rowMeans(as.matrix(esetSel2)), "/")) dist.median <- 1-cor(sweep(as.matrix(esetSel2), 1L, apply(esetSel2, 1, median), "/")) range(dist.no - dist.mean) # [1] -1.477407 0.000000 range(dist.no - dist.median) # [1] -1.349419 0.000000 range(dist.mean - dist.median) # [1] -0.5419534 0.6269875
2. Euclidean distance
dist.no <- dist(as.matrix(esetSel2)) dist.mean <- dist(sweep(as.matrix(esetSel2), 1L, rowMeans(as.matrix(esetSel2)))) dist.median <- dist(sweep(as.matrix(esetSel2), 1L, apply(esetSel2, 1, median))) range(dist.no - dist.mean) # [1] 7.198864e-05 2.193487e+01 range(dist.no - dist.median) # [1] -0.3715231 21.9320846 range(dist.mean - dist.median) # [1] -0.923717629 -0.000088385
Centering does affect the Euclidean distance.
dist.mean <- dist(sweep(as.matrix(esetSel2), 1L, rowMeans(as.matrix(esetSel2)), "/")) dist.median <- dist(sweep(as.matrix(esetSel2), 1L, apply(esetSel2, 1, median), "/")) range(dist.no - dist.mean) # [1] 0.7005071 24.0698991 range(dist.no - dist.median) # [1] 0.636749 24.068920 range(dist.mean - dist.median) # [1] -0.22122869 0.02906131
And scaling affects Euclidean distance too.
How about centering / scaling genes on array clustering?
dist.no <- dist(t(as.matrix(esetSel2))) dist.mean <- dist(t(sweep(as.matrix(esetSel2), 1L, rowMeans(as.matrix(esetSel2))))) dist.median <- dist(t(sweep(as.matrix(esetSel2), 1L, apply(esetSel2, 1, median)))) range(dist.no - dist.mean) # 0 0 range(dist.no - dist.median) # 0 0 range(dist.mean - dist.median) # 0 0 dist.mean <- dist(t(sweep(as.matrix(esetSel2), 1L, rowMeans(as.matrix(esetSel2)), "/"))) dist.median <- dist(t(sweep(as.matrix(esetSel2), 1L, apply(esetSel2, 1, median), "/"))) range(dist.no - dist.mean) # [1] 1.698960 9.383789 range(dist.no - dist.median) # [1] 1.683028 9.311603 range(dist.mean - dist.median) # [1] -0.09139173 0.02546394
Euclidean distance and Pearson correlation relationship
http://analytictech.com/mb876/handouts/distance_and_correlation.htm. In summary,
[math]\displaystyle{ r(X, Y) = 1 - \frac{d^2(X, Y)}{2n} }[/math]
where [math]\displaystyle{ r(X, Y) }[/math] is the Pearson correlation of variables X and Y and [math]\displaystyle{ d^2(X, Y) }[/math] is the squared Euclidean distance of X and Y.
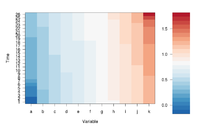
Simple image plot using image() function
https://chitchatr.wordpress.com/2010/07/01/matrix-plots-in-r-a-neat-way-to-display-three-variables/
### Create Matrix plot using colors to fill grid
# Create matrix. Using random values for this example.
rand <- rnorm(286, 0.8, 0.3)
mat <- matrix(sort(rand), nr=26)
dim(mat) # Check dimensions
# Create x and y labels
yLabels <- seq(1, 26, 1)
xLabels <- c("a", "b", "c", "d", "e", "f", "g", "h", "i",
"j", "k");
# Set min and max values of rand
min <- min(rand, na.rm=T)
max <- max(rand, na.rm=T)
# Red and green range from 0 to 1 while Blue ranges from 1 to 0
ColorRamp <- rgb(seq(0.95,0.99,length=50), # Red
seq(0.95,0.05,length=50), # Green
seq(0.95,0.05,length=50)) # Blue
ColorLevels <- seq(min, max, length=length(ColorRamp))
# Set layout. We are going to include a colorbar next to plot.
layout(matrix(data=c(1,2), nrow=1, ncol=2), widths=c(4,1),
heights=c(1,1))
#plotting margins. These seem to work well for me.
par(mar = c(5,5,2.5,1), font = 2)
# Plot it up!
image(1:ncol(mat), 1:nrow(mat), t(mat),
col=ColorRamp, xlab="Variable", ylab="Time",
axes=FALSE, zlim=c(min,max),
main= NA)
# Now annotate the plot
box()
axis(side = 1, at=seq(1,length(xLabels),1), labels=xLabels,
cex.axis=1.0)
axis(side = 2, at=seq(1,length(yLabels),1), labels=yLabels, las= 1,
cex.axis=1)
# Add colorbar to second plot region
par(mar = c(3,2.5,2.5,2))
image(1, ColorLevels,
matrix(data=ColorLevels, ncol=length(ColorLevels),nrow=1),
col=ColorRamp,xlab="",ylab="",xaxt="n", las = 1)
If we define ColorRamp variable using the following way, we will get the 2nd plot.
require(RColorBrewer) # get brewer.pal() ColorRamp <- colorRampPalette( rev(brewer.pal(9, "RdBu")) )(25)
Note that
- colorRampPalette() is an R's built-in function. It interpolate a set of given colors to create new color palettes. The return is a function that takes an integer argument (the required number of colors) and returns a character vector of colors (see rgb()) interpolating the given sequence (similar to heat.colors() or terrain.colors()).
# An example of showing 50 shades of grey in R
greys <- grep("^grey", colours(), value = TRUE)
length(greys)
# [1] 102
shadesOfGrey <- colorRampPalette(c("grey0", "grey100"))
shadesOfGrey(2)
# [1] "#000000" "#FFFFFF"
# And 50 shades of grey?
fiftyGreys <- shadesOfGrey(50)
mat <- matrix(rep(1:50, each = 50))
image(mat, axes = FALSE, col = fiftyGreys)
box()
- (For dual channel data) brewer.pal(9, "RdBu") creates a diverging palette based on "RdBu" with 9 colors. See help(brewer.pal, package="RColorBrewer") for a list of palette name. The meaning of the palette name can be found on colorbrew2.org website. In genomics, we will add rev() such as rev(brewer.pal(9, "RdBu")).
- (For single channel data) brewer.pal(9, "Blues") is good. See an example.
gplots package and heatmap.2()
The following example is extracted from DESeq2 package.
## ----loadDESeq2, echo=FALSE----------------------------------------------
# in order to print version number below
library("DESeq2")
## ----loadExonsByGene, echo=FALSE-----------------------------------------
library("parathyroidSE")
library("GenomicFeatures")
data(exonsByGene)
## ----locateFiles, echo=FALSE---------------------------------------------
bamDir <- system.file("extdata",package="parathyroidSE",mustWork=TRUE)
fls <- list.files(bamDir, pattern="bam$",full=TRUE)
## ----bamfilepaired-------------------------------------------------------
library( "Rsamtools" )
bamLst <- BamFileList( fls, yieldSize=100000 )
## ----sumOver-------------------------------------------------------------
library( "GenomicAlignments" )
se <- summarizeOverlaps( exonsByGene, bamLst,
mode="Union",
singleEnd=FALSE,
ignore.strand=TRUE,
fragments=TRUE )
## ----libraries-----------------------------------------------------------
library( "DESeq2" )
library( "parathyroidSE" )
## ----loadEcs-------------------------------------------------------------
data( "parathyroidGenesSE" )
se <- parathyroidGenesSE
colnames(se) <- se$run
## ----fromSE--------------------------------------------------------------
ddsFull <- DESeqDataSet( se, design = ~ patient + treatment )
## ----collapse------------------------------------------------------------
ddsCollapsed <- collapseReplicates( ddsFull,
groupby = ddsFull$sample,
run = ddsFull$run )
## ----subsetCols----------------------------------------------------------
dds <- ddsCollapsed[ , ddsCollapsed$time == "48h" ]
## ----subsetRows, echo=FALSE----------------------------------------------
idx <- which(rowSums(counts(dds)) > 0)[1:4000]
dds <- dds[idx,]
## ----runDESeq, cache=TRUE------------------------------------------------
dds <- DESeq(dds)
rld <- rlog( dds)
library( "genefilter" )
topVarGenes <- head( order( rowVars( assay(rld) ), decreasing=TRUE ), 35 )
## ----beginner_geneHeatmap, fig.width=9, fig.height=9---------------------
library(RColorBrewer)
library(gplots)
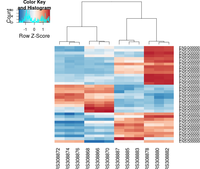
heatmap.2( assay(rld)[ topVarGenes, ], scale="row",
trace="none", dendrogram="column",
col = colorRampPalette( rev(brewer.pal(9, "RdBu")) )(255))
heatmap.2() vs heatmap()
It looks the main difference is heatmap.2() can produce color key on the top-left corner. See Heatmap in R: Static and Interactive Visualization.
Self-defined distance/linkage method
heatmap.2(..., hclustfun = function(x) hclust(x,method = 'ward.D2'), ...)
Missing data
- If dist() does not have NA, we just need to add na.color='grey' to heatmap.2()
- heatmap由于有太多NA无法聚类原因和解决方法
Generate sequential colors & grDevices::colorRampPalette()
?colorRampPalette. See an example Building heatmap with R.
require(RColorBrewer) # brewer.pal ColorRamp <- colorRampPalette( brewer.pal(9, "Blues") )(25) # The above will generate 25 colors by interpolating the colors # defined by brewer.pal(9, "Blues") heatmap.2(..., col = ColorRamp)
Change breaks in scale
https://stackoverflow.com/questions/17820143/how-to-change-heatmap-2-color-range-in-r
Con: it'll be difficult to interpret the heatmap
Font size, rotation
See the help page
cexCol=.8 # reduce the label size from 1 to .8
offsetCol=0 # reduce the offset space from .5 to 0
adjRow, adjCol # similar to offSetCol ??
# 2-element vector giving the (left-right, top-bottom) justification of row/column labels
adjCol=c(1,0) # align to top; only meaningful if we rotate the labels
adjCol=c(0,1) # align to bottom; some long text may go inside the figure
adjCol=c(1,1) # how to explain it?
srtCol=45 # Rotate 45 degrees
keysize=2 # increase the keysize from the default 1.5
key = TRUE # default
key.xlab=NA # default is NULL
key.title=NA
Color labels and side bars
https://stackoverflow.com/questions/13206335/color-labels-text-in-r-heatmap. See the options in an example in ?heatmap.2.
- colRow, colCol
- RowSideColors, ColSideColors
## Color the labels to match RowSideColors and ColSideColors
hv <- heatmap.2(x, col=cm.colors(255), scale="column",
RowSideColors=rc, ColSideColors=cc, margin=c(5, 10),
xlab="specification variables", ylab= "Car Models",
main="heatmap(<Mtcars data>, ..., scale=\"column\")",
tracecol="green", density="density", colRow=rc, colCol=cc,
srtCol=45, adjCol=c(0.5,1))
Moving colorkey
Dendrogram width and height
# Default lhei <- c(1.5, 4) lwid <- c(1.5, 4)
Note these are relative. Recall heatmap.2() makes a 2x2 grid: color key, dendrograms (left & top) and the heatmap (right & bottom).
Modify the margins for column/row names
# Default margins <- c(5, 5) # (column, row)
Note par(mar) does not work.
White strips (artifacts)
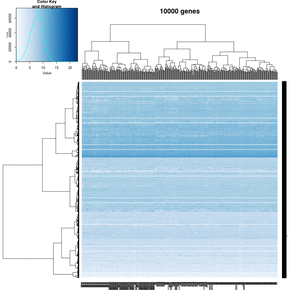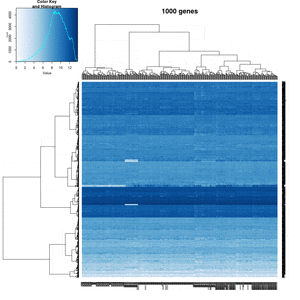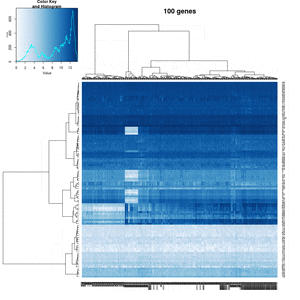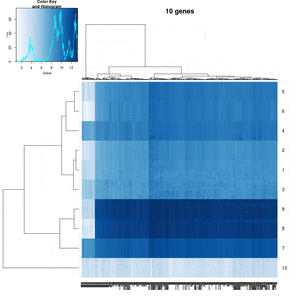
On my Linux (Dell Precision T3500, NVIDIA GF108GL, Quadro 600, 1920x1080), the heatmap shows several white strips when I set a resolution 800x800 (see the plot of 10000 genes shown below). Note if I set a higher resolution 1920x1920, the problem is gone but the color key map will be quite large and the text font will be small.
On MacBook Pro (integrated Intel Iris Pro, 2880x1800), there is no artifact even with 800x800 resolution.
How about saving the plots using
- a different format (eg tiff) or even the lossless compression option - not help
- Cairo package - works. Note that the default background is transparent.
RowSideColors and ColSideColors options
A short tutorial for decent heat maps in R
Annotation
legend("topright",
legend = unique(dat$GO),
col = unique(as.numeric(dat$GO)),
lty= 1,
lwd = 5,
cex=.7)
Another example from video which makes use of an archived package heatmap.plus.
legend(0.8,1,
legend=paste(treatment_times,"weeks"),
fill=treatment_color_options,
cex=0.5)
legend(0.8,0.9,
legend=c("Control","Treatment"),
fill=c('#808080','#FFC0CB'),
cex=0.5)
heatmap.plus()
How to Make an R Heatmap with Annotations and Legend. ColSideColors can be a matrix (n x 2). So it is possible to draw two side colors on the heatmap. Unfortunately the package was removed from CRAN in 2021-04. The package was used by TCGAbiolinks but now this package uses ComplexHeatmap instead.
devtools::install_version("heatmap.plus", "1.3")
Output from heatmap.2 examples
ggplot2 package
- https://learnr.wordpress.com/2010/01/26/ggplot2-quick-heatmap-plotting/
- http://www.kim-herzig.de/2014/06/19/heat-maps-with-ggplot2/
- http://is-r.tumblr.com/post/32387034930/simplest-possible-heatmap-with-ggplot2
- http://smartdatawithr.com/en/creating-heatmaps/#more-875 data values are shown in cells!
ggplot2::geom_tile()
# Suppose dat=[x, y1, y2, y3] is a wide matrix # and we want to make a long matrix like dat=[x, y, val] library(tidyr) dat <- dat %>% pivot_longer(!x, names_to = 'y', values_to='val') ggplot(dat, aes(x, y)) + geom_tile(aes(fill = val), colour = "white") + scale_fill_gradient2(low = "blue", mid = "white", high = "red") + labs(y="Cell Line", fill= "Log GI50") # white is the border color # grey = NA by default # labs(fill) is to change the title # labs(y) is to change the y-axis label
NMF package
aheatmap() function.
- http://nmf.r-forge.r-project.org/aheatmap.html
- http://www.gettinggeneticsdone.com/2015/04/r-user-group-recap-heatmaps-and-using.html
ComplexHeatmap
- Groups of heatmaps
- The color argument can contain a mapping function or a vector of colors. The circlize package (from the same package author) can be used.
- A simple tutorial for a complex ComplexHeatmap
- annotation_label from Chapter 3 Heatmap Annotations
Pros
- Annotation of classes for a new variable.
Correlation matrix
The following code will guarantee the heatmap has a diagonal in the direction of top-left and bottom-right. The row dendrogram will be flipped automatically. There is no need to use cluster_rows = rev(mydend).
mcor <- cor(t(lograt))
colnames(mcor) <- rownames(mcor) <- 1:ncol(mcor)
mydend <- as.dendrogram(hclust(as.dist(1-mcor)))
Heatmap( mcor, cluster_columns = mydend, cluster_rows = mydend,
row_dend_reorder = FALSE, column_dend_reorder = FALSE,
row_names_gp = gpar(fontsize = 6),
column_names_gp = gpar(fontsize = 6),
column_title = "", name = "value")
OncoPrint
- https://jokergoo.github.io/ComplexHeatmap-reference/book/oncoprint.html
- http://qiubio.com/new/book/chapter-08/#oncoprint
- http://blog.thehyve.nl/blog/downloading-data-from-the-cbioportal-oncoprint-view
InteractiveComplexHeatmap
tidyHeatmap
tidyHeatmap. This is a tidy implementation for heatmap. At the moment it is based on the (great) package 'ComplexHeatmap'.
Note: that ComplexHeatmap is on Bioconductor but tidyHeatmap is on CRAN.
By default, .scale = "row". See ?heatmap.
add_tile() to add a column or row (depending on the data) annotation.
cluster_rows=FALSE if we don't want to cluster rows.
BiocManager::install('tidyHeatmap')
library(tidyHeatmap)
library(tidyr)
mtcars_tidy <-
mtcars |>
as_tibble(rownames="Car name") |>
# Scale
mutate_at(vars(-`Car name`, -hp, -vs), scale) |>
# tidyfy
pivot_longer(cols = -c(`Car name`, hp, vs),
names_to = "Property",
values_to = "Value")
# create another variable which will be added next to 'hp'
mtcars_tidy <- mtcars_tidy%>%
mutate(type = `Car name`)
mtcars_tidy$type <- substr(mtcars_tidy$type, 1, 1)
mtcars_tidy
# NA case. Consider the cell on the top-right corner
mtcars_tidy %>% filter(`Car name` == 'Volvo 142E' & Property == 'am')
mtcars_tidy <- mtcars_tidy %>% # Replacing values
mutate(Value = replace(Value,
`Car name` == 'Volvo 142E' & Property == 'am',
NA))
mtcars_tidy %>% filter(`Car name` == 'Volvo 142E' & Property == 'am')
# Re-draw data with missing value
mtcars_tidy |>
heatmap(`Car name`, Property, Value,
palette_value = circlize::colorRamp2(
seq(-2, 2, length.out = 11),
rev(RColorBrewer::brewer.pal(11, "RdBu")))) |>
add_tile(hp) |>
add_tile(type)
# two tiles on rows
mtcars_heatmap <-
mtcars_tidy |>
heatmap(`Car name`, Property, Value,
palette_value = circlize::colorRamp2(
seq(-2, 2, length.out = 11),
rev(RColorBrewer::brewer.pal(11, "RdBu")))) |>
add_tile(hp) |>
add_tile(type)
mtcars_heatmap
# Other useful parameters
# heatmap(, cluster_rows = FALSE)
# heatmap(, .scale = F)
# Note add_tile(var) can decide whether the 'var' should go to
# columns or rows - interesting!
# one tile goes to columns and one tile goes to rows.
tidyHeatmap::pasilla |>
# group_by(location, type) |>
heatmap(
.column = sample,
.row = symbol,
.value = `count normalised adjusted`
) |>
add_tile(condition) |>
add_tile(activation)
Correlation heatmap
Customizable correlation heatmaps in R using purrr and ggplot2
corrplot
This package is used for visualization of correlation matrix. See its vignette and Visualize correlation matrix using correlogram.
ggcorrplot
https://cran.r-project.org/web/packages/ggcorrplot/index.html
ztable
https://cran.r-project.org/web/packages/ztable/index.html
SubtypeDrug: Prioritization of Candidate Cancer Subtype Specific Drugs
https://cran.r-project.org/web/packages/SubtypeDrug/index.html
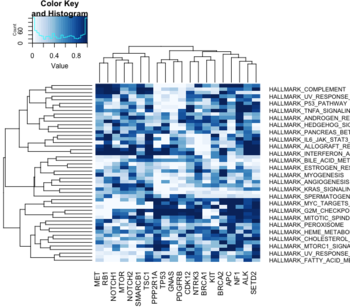
pheatmap
- http://wiki.bits.vib.be/index.php/Use_pheatmap_to_draw_heat_maps_in_R
- Making a heatmap in R with the pheatmap package
- Tips:
- The package was used on the book Modern Statistics for Modern Biology
- Examples:
- PDAC data
- ssgsea
- 生信代码:绘制热图和火山图
- This was used by Orchestrating Single-Cell Analysis with Bioconductor
What is special?
- the color scheme is grey-blue to orange-red. pheatmap() default options, colorRampPalette in R
- able to include class labels in samples and/or genes
- the color key is thin and placed on the RHS (prettier for publications though it could miss information)
- borders for each cell are included (not necessary)
fheatmap
(archived)
Dot heatmap
Office/Excel
Apply a Color Scale Based on Values
Heatmap in the terminal
rasterImage
- http://rfunction.com/archives/2666
- rasterImage(). Note that the parameter interpolate by default is TRUE.
Interactive heatmaps
d3heatmap
This package has been removed from CRAN and archived on 2020-05-24.
A package generates interactive heatmaps using d3.js and htmlwidgets.
The package let you
- Highlight rows/columns by clicking axis labels
- Click and drag over colormap to zoom in (click on colormap to zoom out)
- Optional clustering and dendrograms, courtesy of base::heatmap
The following screenshots shows 3 features.
- Shows the row/column/value under the mouse cursor
- Zoom in a region (click on the zoom-in image will bring back the original heatmap)
- Highlight a row or a column (click the label of another row will highlight another row. Click the same label again will bring back the original image)
heatmaply
- http://moderndata.plot.ly/interactive-heat-maps-for-r/
- heatmaply: an R package for creating interactive cluster heatmaps for online publishing Bioinformatics 2017.
- Use the 'limits' parameter to specify the data range for the scale. See ?heatmaply
This package extends the plotly engine to heatmaps, allowing you to inspect certain values of the data matrix by hovering the mouse over a cell. You can also zoom into a region of the heatmap by drawing a rectangle over an area of your choice.
Installing this package requires to compile some dependent package.
The return object is heatmaply is 'plotly' and 'htmlwidget'. It does not return the ordering of rows/columns. It can not control whether to do clustering (d3heatmap package is better at this).
canvasXpress
- https://cran.r-project.org/web/packages/canvasXpress/index.html
- https://canvasxpress.org/html/heatmap-9.html
InteractiveComplexHeatmap
InteractiveComplexHeatmap, article
Calendar heatmap
Dendrogram
Beautiful dendrogram visualizations in R
Flip dendrogram
https://www.biostars.org/p/279775/
Color labels
library(RColorBrewer)
# matrix contains genomics-style data where columns are samples
# (if otherwise remove the transposition below)
# labels is a factor variable going along the columns of matrix
plotHclustColors <- function(matrix,labels,...) {
colnames(matrix) <- labels
d <- dist(t(matrix))
hc <- hclust(d, method = "ward.D2")
labelColors <- brewer.pal(nlevels(labels),"Set1")
colLab <- function(n) {
if (is.leaf(n)) {
a <- attributes(n)
labCol <- labelColors[which(levels(labels) == a$label)]
attr(n, "nodePar") <- c(a$nodePar, lab.col=labCol)
}
n
}
clusDendro <- dendrapply(as.dendrogram(hc), colLab)
# I change cex because there are lots of samples
op <- par(mar=c(5,3,1,.5)+.1, cex=.3)
plot(clusDendro,...)
par(op)
}
plotHclustColors(genedata, pheno)
Dendrogram with covariates
https://web.stanford.edu/~hastie/TALKS/barossa.pdf#page=41
dendextend* package
- dendextend::plot(, horiz=TRUE) allows to rotate a dendrogram with tips on RHS.
- plot_horiz.dendrogram() allows to rotate a dendrogram with tips on LHS.
- The package has a function tanglegram() to compare two trees of hierarchical clusterings. See this post and its vignette.
- Add colored bars
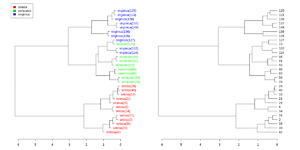
Simplified from dendextend's vignette or Label and color leaf dendrogram.
library(dendextend)
set.seed(1234)
iris <- datasets::iris[sample(150, 30), ] # subset for better view
iris2 <- iris[, -5] # data
species_labels <- iris[, 5] # group for coloring
hc_iris <- hclust(dist(iris2), method = "complete")
iris_species <- levels(species_labels)
dend <- as.dendrogram(hc_iris)
colorCodes <- c("red", "green", "blue")
labels_colors(dend) <- colorCodes[as.numeric(species_labels)][order.dendrogram(dend)]
labels(dend) <- paste0(as.character(species_labels)[order.dendrogram(dend)],
"(", labels(dend), ")")
# We hang the dendrogram a bit:
dend <- hang.dendrogram(dend, hang_height=0.1)
dend <- set(dend, "labels_cex", 1.0)
png("~/Downloads/iris_dextend.png", width = 1200, height = 600)
par(mfrow=c(1,2), mar = c(3,3,1,7))
plot(dend, main = "", horiz = TRUE)
legend("topleft", legend = iris_species, fill = colorCodes)
par(mar=c(3,1,1,5))
plot(as.dendrogram(hc_iris),horiz=TRUE)
dev.off()
Colors
A quick introduction to using color in density plots
http://sharpsightlabs.com/blog/quick-intro-color-density-plot/
display.brewer.pal() and brewer.pal() functions
While brewer.pal() will return colors (in hex) for a certain palette, display.brewer.pal() can display the colors on a graphical device.
library(RColorBrewer) display.brewer.pal(11, "BrBG") # Alternative colors used in correlation matrix display.brewer.pal(9, "Set1") # Up to 9 classes are allowed
Missing data
In the dynamic heatmap tool of BRB-ArrayTools, the missing data is represented by the gray color.
Papers
Double dipping
- Circular analysis
- Selective Inference for Hierarchical Clustering, clusterpval package.
- Are clusterings of multiple data views independent? 2020. multiviewtest package.
- Beyond Sample Splitting: Valid Inference while 'Double Dipping' (Daniela Witten) 2020
- Eleven grand challenges in single-cell data science by Lähnemann, 2020. Search "double".
Healthcare Access and Quality Index - Lancet
http://www.thelancet.com/pdfs/journals/lancet/PIIS0140-6736(17)30818-8.pdf