Regression

From 太極
Jump to navigation Jump to search

Linear Regression

Comic

MSE

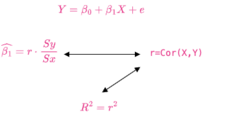
Coefficient of determination R2

  • Relationship in the simple linear regression (intercept is included)
R-squared.png
  • https://en.wikipedia.org/wiki/Coefficient_of_determination.
    • R2 is expressed as the ratio of the explained variance to the total variance.
    • It is a statistical measure of how well the regression predictions approximate the real data points.
    • See the wikipedia page for a list of caveats of R2 including correlation does not imply causation.
R2.png
library(ggplot2)
set.seed(123)
x <- 1:100
y <- x + rnorm(100, sd = 10)
model1 <- lm(y ~ x)
summary(model1)$r.squared  # 0.914

# Now, let's add some noise variables
noise <- matrix(rnorm(100*1000), ncol = 1000)
model2 <- lm(y ~ x + noise)
summary(model2)$r.squared  # 1
[math]\displaystyle{ \begin{align} R^2 &= 1 - \frac{SSE}{SST} \\ &= 1 - \frac{MSE}{Var(y)} \end{align} }[/math]

Pearson correlation and linear regression slope

[math]\displaystyle{ \begin{align} b_1 &= r \frac{S_y}{S_x} \end{align} }[/math]

where [math]\displaystyle{ S_x=\sqrt{\sum(x-\bar{x})^2} }[/math]. 

set.seed(1)
x <- rnorm(10); y <-rnorm(10)
coef(lm(y~x))
# (Intercept)           x
#   0.3170798  -0.5161377

cor(x, y)*sd(y)/sd(x)
# [1] -0.5161377

Different models (in R)

http://www.quantide.com/raccoon-ch-1-introduction-to-linear-models-with-r/

Factor Variables

Regression With Factor Variables

dummy.coef.lm() in R

Extracts coefficients in terms of the original levels of the coefficients rather than the coded variables.

Add Regression Line per Group to Scatterplot

How To Add Regression Line per Group to Scatterplot in ggplot2? 

penguins_df %>%
  ggplot(aes(x=culmen_length_mm, 
             y=flipper_length_mm, 
             color=species))+
  geom_point()+
  geom_smooth(method="lm", se = FALSE)

model.matrix, design matrix

Contrasts in linear regression

  • Page 147 of Modern Applied Statistics with S (4th ed)
  • https://biologyforfun.wordpress.com/2015/01/13/using-and-interpreting-different-contrasts-in-linear-models-in-r/ This explains the meanings of 'treatment', 'helmert' and 'sum' contrasts.
  • A (sort of) Complete Guide to Contrasts in R by Rose Maier 
    mat

##      constant NLvMH  NvL  MvH
## [1,]        1  -0.5  0.5  0.0
## [2,]        1  -0.5 -0.5  0.0
## [3,]        1   0.5  0.0  0.5
## [4,]        1   0.5  0.0 -0.5
mat <- mat[ , -1]

model7 <- lm(y ~ dose, data=data, contrasts=list(dose=mat) )
summary(model7)

## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  118.578      1.076 110.187  < 2e-16 ***
## doseNLvMH      3.179      2.152   1.477  0.14215    
## doseNvL       -8.723      3.044  -2.866  0.00489 ** 
## doseMvH       13.232      3.044   4.347 2.84e-05 ***

# double check your contrasts
attributes(model7$qr$qr)$contrasts
## $dose
##      NLvMH  NvL  MvH
## None  -0.5  0.5  0.0
## Low   -0.5 -0.5  0.0
## Med    0.5  0.0  0.5
## High   0.5  0.0 -0.5

library(dplyr)
dose.means <- summarize(group_by(data, dose), y.mean=mean(y))
dose.means
## Source: local data frame [4 x 2]
## 
##   dose   y.mean
## 1 None 112.6267
## 2  Low 121.3500
## 3  Med 126.7839
## 4 High 113.5517

# The coefficient estimate for the first contrast (3.18) equals the average of 
# the last two groups (126.78 + 113.55 /2 = 120.17) minus the average of 
# the first two groups (112.63 + 121.35 /2 = 116.99).

Multicollinearity

  • A toy example 
    n <- 100
set.seed(1)
x1 <- rnorm(n)
e <- rnorm(n)*.01
y <- x1 + e
cor(y, e)  # 0.00966967
cor(y, x1) # 0.9999
lm(y ~ x1) |> summary()      # p<2e-16

set.seed(2)
x2 <- x1 + rnorm(n)*.1       # x2 = x1 + noise
cor(x1, x2)  # .99
lm(y ~ x1 + x2) |> summary() # x2 insig
lm(y~ x2) |> summary()       # x2 sig

set.seed(3)
x3 <- x1 + rnorm(n)*.0001    # x3 = x1 + tiny noise
cor(x1, x3) # 1
lm(y ~ x1 + x3) |> summary() # both insig. SURPRISE!
lm(y ~ x1) |> summary()

x4 <- x1                     # x4 is exactly equal to x1  
lm(y~ x1 + x4) |> summary()  # x4 coef not defined because of singularities
lm(y~ x4 + x1) |> summary()  # x1 coef not defined because of singularities

    Consider lasso 

    fit <- cv.glmnet(x=cbind(x1, x3, matrix(rnorm(n*10), nr=n)), y=y)
coefficients(fit, s = "lambda.min")
# 13 x 1 sparse Matrix of class "dgCMatrix"
#                      s1
# (Intercept) 0.002797165
# x1          0.970839175
# x3          .          
#             .          

fit <- cv.glmnet(x=cbind(x1, x4, matrix(rnorm(n*10), nr=n)), y=y)
coefficients(fit, s = "lambda.min")
# 13 x 1 sparse Matrix of class "dgCMatrix"
#                       s1
# (Intercept) 2.797165e-03
# x1          9.708392e-01
# x4          6.939215e-18
#             .   

fit <- cv.glmnet(x=cbind(x4, x1, matrix(rnorm(n*10), nr=n)), y=y)
coefficients(fit, s = "lambda.min")
# 13 x 1 sparse Matrix of class "dgCMatrix"
#                      s1
# (Intercept) 2.797165e-03
# x4          9.708392e-01
# x1          6.93 9215e-18
#             .
  • How to Fix in R: not defined because of singularities
  • Multicollinearity in R
  • Detecting multicollinearity — it’s not that easy sometimes
  • alias: Find Aliases (Dependencies) In A Model 
    > op <- options(contrasts = c("contr.helmert", "contr.poly"))
> npk.aov <- aov(yield ~ block + N*P*K, npk)
> alias(npk.aov)
Model :
yield ~ block + N * P * K

Complete :
         (Intercept) block1 block2 block3 block4 block5 N1    P1    K1    N1:P1 N1:K1 P1:K1
N1:P1:K1     0           1    1/3    1/6  -3/10   -1/5      0     0     0     0     0     0

> options(op)

Exposure

https://en.mimi.hu/mathematics/exposure_variable.html

Independent variable = predictor = explanatory = exposure variable

Marginal effects

Confounders, confounding

Simulated data

Question: gene expression ~ age + condition (condition is significant) but gene expression ~ condition (condition is not significant). Releted post: Highly DE genes but small count difference within conditions.

Possible Explanation

  1. Confounding Variable: Age might be a confounding variable, meaning it influences both gene expression and condition. When you include age, you control for its effect, which clarifies the relationship between condition and gene expression.
  2. Interaction Effect: There might be an interaction between age and condition. In the full model, the combined effect of age and condition provides a clearer picture of how condition affects gene expression.
  3. Multicollinearity: It could also indicate multicollinearity, where age and condition are correlated. Including both variables might change the significance levels.

Simulated data

  • Confounding only (covariates). 
    # Simulate data
n <- 100
age <- rnorm(n, mean = 50, sd = 10)  # Continuous variable for age

# Influence condition by age: older individuals more likely to have condition
condition <- ifelse(age > 50, 1, 0) 

# Simulate gene expression with confounding but no interaction or multicollinearity
expression <- 5 + 0.3*age + 2*condition + rnorm(n)

# Create data frame
df <- data.frame(age, condition, expression)
  • Interaction only 
    # Set seed for reproducibility
set.seed(123)

# Simulate data
n <- 100
age <- rnorm(n, mean = 50, sd = 10)  # Continuous variable for age
condition <- rbinom(n, 1, 0.5)       # Binary variable for condition

# Simulate gene expression with interaction, no confounding, no multicollinearity
expression <- 5 + 0.3*age + 2*condition + 0.5*age*condition + rnorm(n)

# Create data frame
df <- data.frame(age, condition, expression)
  • multicollinearity only (covariates) 
    # Set seed for reproducibility
set.seed(123)

# Simulate data
n <- 100
age <- rnorm(n, mean = 50, sd = 10)  # Continuous variable for age
# Create a multicollinear variable that is highly correlated with age
age_collinear <- age + rnorm(n, mean = 0, sd = 2) 

# Binary condition variable, independent of age
condition <- rbinom(n, 1, 0.5)

# Simulate gene expression with no confounding or interaction but with multicollinearity
expression <- 5 + 0.3*age + 0.3*age_collinear + 2*condition + rnorm(n)

# Create data frame
df <- data.frame(age, age_collinear, condition, expression)

# Check multicollinearity
library(car)
vif(lm(expression ~ age + age_collinear + condition, data = df))
# A VIF value above 10 generally indicates high multicollinearity, 
# but even values above 5 might be concerning.
  • Everything 
    # Load necessary library
library(dplyr)

# Set seed for reproducibility
set.seed(123)

# Simulate data
n <- 100
age <- rnorm(n, mean = 50, sd = 10)  # Continuous variable for age
# Influence condition by age: older individuals more likely to have condition
condition <- ifelse(age > 50, 1, 0)  

# Create a multicollinear variable that is highly correlated with age
age_collinear <- age + rnorm(n, mean = 0, sd = 2)

# Simulate gene expression with confounding, multicollinearity, and interaction
expression <- 5 + 0.3*age + 0.3*age_collinear + 2*condition + 0.5*age*condition + rnorm(n)

# Create data frame
df <- data.frame(age, age_collinear, condition, expression)

# Summary of data
summary(df)

# Check multicollinearity
library(car)
vif(lm(expression ~ age + age_collinear + condition, data = df))

Plotting

  • Stratified Scatter Plot 
    plot(df$age, df$expression, col=as.factor(df$condition), pch=16, 
     main="Stratified Plot: Age vs. Expression by Condition", 
     xlab="Age", ylab="Gene Expression")
legend("topright", legend=levels(as.factor(df$condition)), 
       col=1:length(levels(as.factor(df$condition))), 
       pch=16)
  • Pair Plot 
    pairs(~expression + age + condition, data=df, 
      main="Pair Plot: Expression, Age, Condition", 
      col=as.factor(df$condition), pch=16)

Confidence interval vs prediction interval

Confidence intervals tell you about how well you have determined the mean E(Y). Prediction intervals tell you where you can expect to see the next data point sampled. That is, CI is computed using Var(E(Y|X)) and PI is computed using Var(E(Y|X) + e).

Homoscedasticity, Heteroskedasticity, Check model for (non-)constant error variance

Linear regression with Map Reduce

https://freakonometrics.hypotheses.org/53269

Relationship between multiple variables

Visualizing the relationship between multiple variables

Model fitting evaluation, Q-Q plot

Added variable plots

Added Variable Plots/partial-regression plots

Generalized least squares

Reduced rank regression

Singular value decomposition

  • Moore-Penrose matrix inverse in R 
    > a = matrix(c(2, 3), nr=1)
> MASS::ginv(a) * 8 
         [,1]
[1,] 1.230769
[2,] 1.846154  
# Same solution as matlab lsqminnorm(A,b)

> a %*% MASS::ginv(a)
     [,1]
[1,]    1
> a %*% MASS::ginv(a) %*% a
     [,1] [,2]
[1,]    2    3
> MASS::ginv   # view the source code

Mahalanobis distance and outliers detection

Mahalanobis distance

  • The Mahalanobis distance is a measure of the distance between a point P and a distribution D
  • It is a multi-dimensional generalization of the idea of measuring how many standard deviations away P is from the mean of D.
  • The Mahalanobis distance is thus unitless and scale-invariant, and takes into account the correlations of the data set.
  • Distance is not always what it seems

performance::check_outliers() Outliers detection (check for influential observations)

How to Calculate Mahalanobis Distance in R 

set.seed(1234)
x <- matrix(rnorm(200), nc=10)
x0 <- rnorm(10)
mu <- colMeans(x)
mahalanobis(x0, colMeans(x), var(x)) # 17.76527
t(x0-mu) %*% MASS::ginv(var(x)) %*% (x0-mu) # 17.76527

# Variance is not full rank
x <- matrix(rnorm(200), nc=20)
x0 <- rnorm(20)
mu <- colMeans(x)
t(x0-mu) %*% MASS::ginv(var(x)) %*% (x0-mu)
mahalanobis(x0, colMeans(x), var(x))
# Error in solve.default(cov, ...) : 
#   system is computationally singular: reciprocal condition number = 1.93998e-19

Type 1 error

Linear Regression And Type I Error

More Data Can Hurt for Linear Regression

Sometimes more data can hurt!

Estimating Coefficients for Variables in R

Trying to Trick Linear Regression - Estimating Coefficients for Variables in R

Interaction term

Without intercept

lm(formula = y ~ x1 + x2 -1)
# or
lm(formula = y ~ x1 + x2 +0)

Intercept only model and cross-validation

n <- 20
set.seed(1)
x <- rnorm(n)
y <- 2*x + .5*rnorm(n)
plot(x, y)
df <- data.frame(x=x, y=y)
pred <- double(n)
for(i in 1:n) {
  fit <- lm(y ~ 1, data = df[-i, ])
  pred[i] <- predict(fit, df[i, ])
}
plot(y, pred)
cor(y, pred) # -1

How about 1000 simulated data? 

foo <- function(n=3, debug=F) {
  x <- rnorm(n)
  y <- 2*x + .5*rnorm(n)
  df <- data.frame(x=x, y=y)
  pred <- double(n)
  for(i in 1:n) {
    fit <- lm(y ~ 1, data = df[-i, ])
    pred[i] <- predict(fit, df[i, ])
  }
  if (debug) {
    cat("num=", n*sum(y*pred)-sum(pred)*sum(y), "\n")
    cat("denom=", sqrt(n*sum(y**2) - sum(y)^2)*sqrt(n*sum(pred**2)-sum(pred)^2), "\n")
    invisible(list(y=y, pred=pred, cor=cor(y, pred)))
  } else {
    cor(y, pred)
  }
}

o <- replicate(1000, foo(n=10))
range(o) # [1] -1 -1
all.equal(o, rep(-1, 1000)) # TRUE

Note the property will not happen in k-fold CV (not LOOCV) 

n <- 20; nfold <- 5
set.seed(1)
x <- rnorm(n)
y <- 2*x + .5*rnorm(n)
#plot(x, y)
df <- data.frame(x=x, y=y)
set.seed(1)
folds <- split(sample(1:n), rep(1:nfold, length = n))
pred <- double(n)
for(i in 1:nfold) {
  fit <- lm(y ~ 1, data = df[-folds[[i]], ])
  pred[folds[[i]]] <- predict(fit, df[folds[[i]], ])
}
plot(y, pred)
cor(y, pred) # -0.6696743

See also

lm.fit and multiple responses/genes

Logistic regression

Interpretation

  • Logistic regressions is to model the log odds of an event, rather than the probability of an event, based on a linear combination of predictor variables. log(p/(1-p)) = beta*x.
  • Logistic regression is not advanced ‘machine learning’ or ‘artificial intelligence’. It is possible to obtain the same coefficients from the glm() function by transforming the data following the Binomial regression “recipe” and then using lm() repeated times until reaching convergence.
  • Odds Are You’re Using Probabilities to Describe Event Outcomes
  • The difference between odds and odds ratio in logistic regression.
    • Odds of some event = p/(1-p) = exp(Xb)
    • Odds ratio for variable X = Odds1/Odds2 = odds(b(X+1)) / odds(bX) = exp(b(X+1)) / exp(Xb) = exp(b). This interpretation mainly applies to binary predictors.
    • If the odds ratio is greater than 1, then the independent variable is positively associated with the dependent variable. This means that an increase in the independent variable will lead to an increase in the odds of the dependent variable occurring.
    • If the odds ratio is less than 1, then the independent variable is negatively associated with the dependent variable. This means that an increase in the independent variable will lead to a decrease in the odds of the dependent variable occurring.
  • How to Interpret Logistic Regression Coefficients (With Example) including binary predictor and continuous predictor variable. There is no need to use the convoluted term 'odds ratio' .
    • [math]\displaystyle{ e^\beta }[/math] = Average Change(division) in Odds of an event (Odds1 / Odds2) for every one-unit increase of the predictor.
    • β = Average Change in Log Odds of Response Variable
    • Binary predictor variable case (female/male).
      • If [math]\displaystyle{ e^\beta = 0.57 }[/math], it means males have 0.57 times the odds of passing the exam relative to females (assuming male is coded as 1 and female as 0). We could also say that males have [math]\displaystyle{ (1 - e^{\beta}) = (1 – 0.57) = }[/math] 43% lower odds of passing the exam than females.
      • If [math]\displaystyle{ e^\beta = 1.5 }[/math], it means males are 1.5 times more likely to pass the exam than females. In other words, the odds of a male passing the exam are 1.5 times the odds of a female passing the exam.
    • Continuous predictor variable case (number of practice exams taken). If [math]\displaystyle{ e^\beta = e^{1.13} = 3.09 }[/math], it means additional practice exam is associated with a tripling of the odds of passing the final exam.
      • Or each additional practice exam taken is associated with (3.09-1)*100=209% increase in the odds of passing the exam, assuming the other variables are held unchanged.
      • If someone originally had a 50% chance of passing (odds of 1:1), taking one more practice exam would increase their odds to 3.09. This translates to a roughly 75.6% chance/probability of passing after taking one more exam 3.09 = p/(1-p) -> p=exp(beta)/(1+exp(beta))=3.09/(4.09)=75.6%.
    • Continuous predictor variable. If [math]\displaystyle{ e^\beta = e^{-.38} = 0.68 }[/math], it means if the predictor variable (number of practice exams) increases by one unit, the odds of passing the exam decrease by approximately 32%.
      • If someone originally had a 50% chance of passing (odds of 1:1), what would be the chance of passing an exam for taking an additional practice exam? 0.68 = p/(1-p), p=0.405. Therefore, after taking one more practice exam, the chance of passing the exam decreases to approximately 40.5%.
  • Interpret Logistic Regression Coefficients (For Beginners).
    • Increasing the predictor by 1 unit (or going from 1 level to the next) multiplies the odds of having the outcome by exp(β).
    • exp^β is the odds ratio that associates smoking to the risk of heart disease.
    • If exp^β = exp^0.38 = 1.46, the smoking group has a 1.46 times the odds of the non-smoking group of having heart disease.
    • The smoking group has 46% (1.46 – 1 = 0.46) more odds of having heart disease than the non-smoking group.
    • If β = – 0.38, then exp^β = 0.68 and the interpretation becomes: smoking is associated with a 32% (1 – 0.68 = 0.32) reduction in the relative risk of heart disease.
    • If β = 0, then exp^β =1, the smoking group has the same odds as the non-smoking group of having heart disease.
    • How to interpret the intercept? If the intercept has a negative sign: then the probability of having the outcome will be < 0.5.
  • A Simple Interpretation of Logistic Regression Coefficients.
    • Odds = p/(1-p), p is the probability that an event occurs. For example, if you roll a six-sided die, the odds of rolling a 6 is 1 to 5 (abbreviated 1:5).
    • logit(p) = log-odds ratio.
    • A 1 unit increase in X₁ will result in beta increase in the log-odds ratio of success : failure.
    • For a one-unit increase of the predictor variable, the odds of the event happening increase by exp(beta)
    • In other words, if exp(b)=1.14, it means increasing studying hour by 1 unit will have a 14% increase in the odds of passing the exam (assuming that the variable female remains fixed) where p = the probability of passing an exam. For every one unit increase in the independent variable, the odds of passing the test increase by a factor of 1.14. In other words, if a student studies for one hour more than another student, they are 1.14 times more likely to pass the test. For example, if the probability of passing the test was initially 50%, then after 1 unit increase in study hours, the odds of passing the test is multiplied by 1.14, the new probability of passing the test would be 57% (50 * 1.14 = 57 %).
    • If however exp(b)=0.68, it means for every 1 unit increase in study hours, the odds of passing the exam decreased by a factor of 0.68. For example, if the odds of passing the exam were initially 50%, then after a one-unit increase in study hours, the new odds of passing the exam would be 34% (50* * 0.68 = 34%).
  • How to Interpret Logistic Regression Coefficients
  • Interpretation: consider X=(intercept, x), beta = (beta0, beta1) and assume x = 0/1. Then logit(beta0) is the percentage of positive results in Y when x = 0, and logit(beta0 + beta1) is the percentage of positive results in Y when x =1. Again, exp(beta1) is the odds ratio. The probabilities can be predicted by using the formula 1 / (1 + exp (-(b0 + b1*x)) )

Hosmer–Lemeshow test for goodness-of-fit

Multinomial logistic regression

Generalized linear models

  • ?glm, ?family
  • Examples: 
    glm(counts ~ outcome + treatment, family = poisson())

glm(Postwt ~ Prewt + Treat + offset(Prewt),
                family = gaussian, data = anorexia)

glm(lot1 ~ log(u), data = clotting, family = Gamma)
  • Summarize
    Probability Distribution family Parameter Typical Use Cases Default Link Function
    Gaussian gaussian (default) Continuous, normally distributed data Identity
    Binomial binomial Binary (yes/no) data or proportions Logit,
    (probit, cloglog)
    Poisson poisson Count data following Poisson distribution Log
    Gamma Gamma Continuous, positive data following gamma distribution Inverse
    Inverse Gaussian inverse.gaussian Continuous, positive data following inverse Gaussian distribution 1/mu^2
    Tweedie tweedie Flexible distribution for various data types Power value

Poisson regression

A Gentle Introduction to Poisson Regression for Count Data: School’s Out, Job Offers Incoming!

Plot

Nomogram

  • Nomogram
  • Components of a Nomogram:
    • Axes: A nomogram consists of multiple scales, each representing a variable in the model.
    • Lines: Straight lines are drawn between the scales to determine the predicted outcome.
    • Points: Points are assigned to each predictor variable based on its value, and these points are summed to provide an overall score, which can then be translated into a probability of the outcome. Note, the individual data points do not have to be plotted on the nomogram itself.
  • How It Works:
    • Input Variables: Each input variable has its own scale on the nomogram. For example, age, tumor size, and gender might be different scales.
    • Point Assignment: For each input variable, a certain number of points is assigned based on its value. These points are located on a “points” axis, which is summed up to obtain a total score.
    • Outcome Probability: The total score corresponds to the probability of the event of interest (e.g., survival probability) using a separate axis. If you wanted to assess the accuracy of a nomogram, you might create a separate calibration plot where observed outcomes (from real data) are plotted against predicted probabilities (from the nomogram).
  • Simple Example: Let’s consider a simplified example where a nomogram is used to predict the probability of a disease based on two factors: Age and Blood Pressure (BP).
    1. Age Scale: This scale might range from 20 to 80 years.
    2. BP Scale: This scale might range from 100 to 180 mmHg.
  • Nomogram plot
    Nomogram.png

Calibration Plot

Calibration plots are used to compare predicted probabilities from a model (like a logistic regression or a nomogram) with the actual observed outcomes. They help assess the accuracy of a prediction model.

Decision Curve Analysis (DCA)

Decision curve analysis evaluates the clinical usefulness of prediction models by comparing the net benefit of using the model to make decisions at various threshold probabilities.

Forest Plot

Forest plots are commonly used in meta-analysis to display the estimated effects from multiple studies.

Logistic Regression Curve

In binary logistic regression, the logistic curve (or S-curve) is used to model the probability of an event occurring based on a linear combination of predictor variables.

Score Plot (from Principal Component Analysis)

Partial Dependence Plot (PDP)

  • PDPs show the relationship between a predictor variable and the predicted outcome while accounting for the average effect of other predictors in the model.
  • CRAN, github
  • Interpretable Machine Learning by Christoph Molnar
  • Detailed breakdown:
    • How it works: For each value of the predictor variable of interest, the PDP is calculated by averaging the model’s predictions over the range of values for the other predictor variables. This isolates the effect of the predictor variable of interest from the effects of the other predictors.
    • Types of PDPs:
      • Univariate PDP: Shows the effect of a single predictor variable on the prediction.
      • Bivariate PDP: Shows the effect of two predictor variables together on the prediction.
  • Linear regression with two predictors X1 and X2 
    # Load necessary libraries
library(ggplot2)
library(gridExtra)

# Generate sample data
set.seed(123)
n <- 100
X1 <- rnorm(n)
X2 <- rnorm(n)
Y <- 5 + 2*X1 + 3*X2 + rnorm(n)

# Fit a linear regression model
model <- lm(Y ~ X1 + X2)

# Predict function for new data
predict_model <- function(new_data) {
  predict(model, new_data)
}

# Partial Dependence Plot for X1
pdp_X1 <- function(X1_values) {
  new_data <- data.frame(X1 = X1_values, X2 = mean(X2))
  predictions <- predict_model(new_data)
  data.frame(X1 = X1_values, Prediction = predictions)
}

# Partial Dependence Plot for X2
pdp_X2 <- function(X2_values) {
  new_data <- data.frame(X1 = mean(X1), X2 = X2_values)
  predictions <- predict_model(new_data)
  data.frame(X2 = X2_values, Prediction = predictions)
}

# Generate values for PDPs
X1_values <- seq(min(X1), max(X1), length.out = 100)
X2_values <- seq(min(X2), max(X2), length.out = 100)

# Create PDP data
pdp_X1_data <- pdp_X1(X1_values)
pdp_X2_data <- pdp_X2(X2_values)

# Plot PDPs
p1 <- ggplot(pdp_X1_data, aes(x = X1, y = Prediction)) +
  geom_line() +
  ggtitle("Partial Dependence Plot for X1") +
  xlab("X1") + ylab("Predicted Y")

p2 <- ggplot(pdp_X2_data, aes(x = X2, y = Prediction)) +
  geom_line() +
  ggtitle("Partial Dependence Plot for X2") +
  xlab("X2") + ylab("Predicted Y")

# Display plots
grid.arrange(p1, p2, ncol = 2)
  • Cox regression.
    • Risk score [math]\displaystyle{ = \exp(\beta X) }[/math]. It is closely related to the hazard function h(t|X)=h0(t)exp(b*X).
    • If X=1, we obtained the HR. The hazard ratio (HR) represents the effect of a one-unit change in the predictor on the hazard.
    library(survival)
library(ggplot2)

set.seed(123)
n <- 200
X1 <- rnorm(n)
X2 <- rnorm(n)
time <- rexp(n, exp(0.5*X1 - 0.3*X2))
status <- sample(0:1, n, replace = TRUE)

# Fit the Cox model
cox_model <- coxph(Surv(time, status) ~ X1 + X2)

# Define the predictor range

# Define the range of values for X1
X1_values <- seq(min(X1), max(X1), length.out = 100)

# Calculate the mean of X2
X2_mean <- mean(X2)

# Function to compute the risk score
compute_risk_score <- function(X1_values, model, X2_mean) {
  new_data <- data.frame(X1 = X1_values, X2 = X2_mean)
  risk_score <- exp(predict(model, newdata = new_data, type = "lp")) # default
  # OR
  # risk_score <- predict(model, newdata = new_data, type = "risk") # risk score
  data.frame(X1 = X1_values, RiskScore = risk_score)
}

pdp_X1_data <- compute_risk_score(X1_values, cox_model, X2_mean)

# The plot shows how the risk score changes with the predictor X1, holding X2 constant.
# The baseline hazard function  h_0(t)  is not included in the PDP, as we are focusing 
#   on the relative effects of predictors.
# Plot PDP for X1
ggplot(pdp_X1_data, aes(x = X1, y = HazardRatio)) +
  geom_line() +
  ggtitle("Partial Dependence Plot for X1 in Cox Regression") +
  xlab("X1") +
  ylab("Risk score")

    Use survival probability instead of risk score. 

    # Define a function to compute survival probabilities
compute_survival_prob <- function(X1_values, model, X2_mean) {
  new_data <- data.frame(X1 = X1_values, X2 = X2_mean)
  risk_score <- exp(predict(model, newdata = new_data, type = "lp")) # default
  # OR
  # risk_score <- predict(model, newdata = new_data, type = "risk")
  survival_prob <- baseline_survival_prob ^ risk_score
  return(survival_prob)
}

# Approximate survival probability (assuming a fixed time t for illustration)
# You would need to adjust this based on your actual survival analysis
# For demonstration purposes, we assume baseline survival probability at time t
baseline_survival_prob <- 0.9  # S0(t) 

# Compute survival probabilities for the range of X1 values
survival_probs <- compute_survival_prob(X1_values, cox_model, X2_mean)

library(ggplot2)

# Create a data frame for plotting
pdp_data <- data.frame(X1 = X1_values, SurvivalProbability = survival_probs)

# Plot the survival function vs. predictor
ggplot(pdp_data, aes(x = X1, y = SurvivalProbability)) +
  geom_line() +
  ggtitle("Partial Dependence Plot: Survival Function vs Predictor") +
  xlab("Predictor (X1)") +
  ylab("Survival Probability")

Quantile regression

  • Quantile regression is a type of regression analysis in which quantiles of the dependent variable (unlike traditional linear regression, which models the mean of the dependent variable) are modeled as a function of independent variables. This allows for a better understanding of the distribution of the dependent variable, especially when the distribution is skewed or has outliers.
  • https://en.wikipedia.org/wiki/Quantile_regression
  • Basic Quantile Regression
  • QUANTILE REGRESSION (HOME MADE, PART 2) 
    library(quantreg)
set.seed(123)
x <- rnorm(100)
y <- x + rnorm(100, mean = 0, sd = 2)
y[1:10] <- y[1:10] + 10 # first 10 are outliers

# Fit a traditional linear regression model
fit_lm <- lm(y ~ x)

# Fit a quantile regression model for the 50th percentile
fit_qr <- rq(y ~ x, tau = 0.5)

fit_lm$coefficients
# (Intercept)           x 
#   0.7961233   0.8759269 
fit_qr$coefficients
# (Intercept)           x 
#   0.0772395   1.0058387 

plot(x, y)
points(x[1:10], y[1:10], col='red', pch=16)
abline(fit_lm)
abline(fit_qr, col = 'blue')
  • Navigating Quantile Regression with R: A Comprehensive Guide

Isotonic regression

Piecewise linear regression

Support vector regression

  • An Introduction to Support Vector Regression (SVR).
    • The goal of SVR is to find a function that approximates the relationship between the input and output variables in the training data, with an acceptable amount of error. This is done by mapping the input data into a high-dimensional feature space using a kernel function, and then finding a linear regression function in that space that fits the data with a specified margin of error.
    • SVR has been proven to be an effective tool in real-value function estimation, and like SVM, it is characterized by the use of kernels, sparse solution, and VC control of the margin and the number of support vectors.
  • Awad in Springer

Model Misspecification

Robust regression

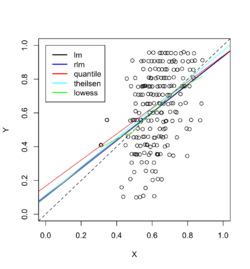
Example 1: data with outliers

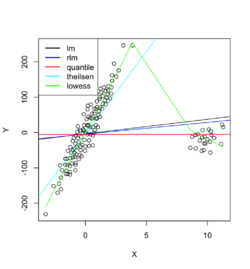
Below is an example where we fit the data using linear regression, robust linear regression (Robust against outliers and deviations from normality), quantile regression (Estimates conditional quantiles of the response variable), Theil-sen regression (Computes the median of pairwise slopes between data points) and Local polynomial regression (non-linear relationships and adapts to local variations).

DataOutliers.png

Example 2: data with outliers

The raw data are 'recovered' from the page Dealing with Outliers Using Three Robust Linear Regression Models. In this case, Theil-sen regression performed better than the other methods.

DataOutliers2.png

Choose variables

Variable selection in linear regression models: Choosing the best subset is not always the best choice 2023

Stepwise selection of variables

Stepwise selection of variables in regression is Evil

GEE/generalized estimating equations

See Longitudinal data analysis.

Deming regression

Deming regression

Tweedie regression

Model selection, AIC and Tweedie regression

Causal inference

  • The intuition behind inverse probability weighting in causal inference*, Confounding in causal inference: what is it, and what to do about it?
    Outcome [math]\displaystyle{ \begin{align} Y = T*Y(1) + (1-T)*Y(0) \end{align} }[/math]
    Causal effect (unobserved) [math]\displaystyle{ \begin{align} \tau = E(Y(1) -Y(0)) \end{align} }[/math]
    where [math]\displaystyle{ E[Y(1)] }[/math] referred to the expected outcome in the hypothetical situation that everyone in the population was assigned to treatment, [math]\displaystyle{ E[Y|T=1] }[/math] refers to the expected outcome for all individuals in the population who are actually assigned to treatment... The key is that the value of [math]\displaystyle{ E[Y|T=1]−E[Y|T=0] }[/math] is only equal to the causal effect, [math]\displaystyle{ E[Y(1)−Y(0)] }[/math] if there are no confounders present.
    Inverse-probability weighting removes confounding by creating a “pseudo-population” in which the treatment is independent of the measured confounders... Add a larger weight to the individuals who are underrepresented in the sample and a lower weight to those who are over-represented... propensity score P(T=1|X), logistic regression, stabilized weights.
  • A Crash Course in Causality: Inferring Causal Effects from Observational Data (Coursera) which includes Inverse Probability of Treatment Weighting (IPTW). R packages used: tableone, ipw, sandwich, survey.

Mendelian Randomization

Seemingly unrelated regressions/SUR

  • Seemingly unrelated regressions from wikipedia
    • Advantages: The SUR model is useful when the error terms of the regression equations are correlated with each other. In this case, the ordinary least squares (OLS) estimator is inefficient and inconsistent. The SUR model can provide more efficient and consistent estimates of the regression coefficients
    • Disadvantages: One disadvantage of using the SUR model is that it requires the assumption that the error terms are correlated across equations. If this assumption is not met, then the SUR model may not provide more efficient estimates than estimating each equation separately1. Another disadvantage of using the SUR model is that it can be computationally intensive and may require more time to estimate than estimating each equation separately
  • Seemingly Unrelated Regression (SUR/SURE)
  • How can I perform seemingly unrelated regression in R?
  • spsur package
  • Equations for the simplest case:
    [math]\displaystyle{ \begin{align} y_1 &= b_1x_1 + b_2x_2 + u_1 \\ y_2 &= b_3x_1 + b_4x_2 + u_2 \end{align} }[/math]
Retrieved from "https://wiki.taichimd.us/index.php?title=Regression&oldid=40799"