Statistics: Difference between revisions
| (254 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
* [https://en.wikipedia.org/wiki/Egon_Pearson Egon Pearson] (1895-1980): son of Karl Pearson | * [https://en.wikipedia.org/wiki/Egon_Pearson Egon Pearson] (1895-1980): son of Karl Pearson | ||
* [https://en.wikipedia.org/wiki/Jerzy_Neyman Jerzy Neyman] (1894-1981): type 1 error | * [https://en.wikipedia.org/wiki/Jerzy_Neyman Jerzy Neyman] (1894-1981): type 1 error | ||
* [https://www.youtube.com/playlist?list=PLt_pNkbycxqahVksaNnjz3M6759xHIZ-r Ten Statistical Ideas that Changed the World] | |||
== The most important statistical ideas of the past 50 years == | == The most important statistical ideas of the past 50 years == | ||
[https://arxiv.org/pdf/2012.00174.pdf What are the most important statistical ideas of the past 50 years?], [https://www.tandfonline.com/doi/full/10.1080/01621459.2021.1938081 JASA 2021] | [https://arxiv.org/pdf/2012.00174.pdf What are the most important statistical ideas of the past 50 years?], [https://www.tandfonline.com/doi/full/10.1080/01621459.2021.1938081 JASA 2021] | ||
= | = Some Advice = | ||
http://www.nature.com/collections/qghhqm | * [http://www.nature.com/collections/qghhqm Statistics for biologists] | ||
* [https://www.bmj.com/content/379/bmj-2022-072883 On the 12th Day of Christmas, a Statistician Sent to Me . . .], [https://tinyurl.com/yzpv2uu6 The abridged 1-page print version]. | |||
= Data = | = Data = | ||
| Line 17: | Line 19: | ||
[https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1009819 Ten simple rules for initial data analysis] | [https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1009819 Ten simple rules for initial data analysis] | ||
== Exploratory Analysis == | == Types of probabilities == | ||
[https://soroosj.netlify.app/2020/09/26/penguins-cluster/ Kmeans Clustering of Penguins] | See this [https://twitter.com/5_utr/status/1688730481171279872?s=20 illustration] | ||
== Exploratory Analysis (EDA) == | |||
* [https://soroosj.netlify.app/2020/09/26/penguins-cluster/ Kmeans Clustering of Penguins] | |||
* [https://cran.r-project.org/web/packages/skimr/index.html skimr] package | |||
** [https://github.com/agstn/dataxray dataxray] package - An interactive table interface (of skimr) for data summaries. [https://www.r-bloggers.com/2023/01/cut-your-eda-time-into-5-minutes-with-exploratory-dataxray-analysis-edxa/ Cut your EDA time into 5 minutes with Exploratory DataXray Analysis (EDXA)] | |||
* [https://medium.com/@jchen001/20-useful-r-packages-you-may-not-know-about-54d57fe604f3 20 Useful R Packages You May Not Know Of] | |||
* [https://twitter.com/ItaiYanai/status/1612627199332433922 12 guidelines for data exploration and analysis with the right attitude for discovery] | |||
== Kurtosis == | == Kurtosis == | ||
| Line 24: | Line 33: | ||
== Phi coefficient == | == Phi coefficient == | ||
[https://finnstats.com/index.php/2021/07/24/how-to-calculate-phi-coefficient-in-r/ How to Calculate Phi Coefficient in R]. It is a measurement of the degree of association between two binary variables. | <ul> | ||
<li>[https://en.wikipedia.org/wiki/Phi_coefficient Phi coefficient]. Its values is [-1, 1]. A value of zero means that the binary variables are not positively or negatively associated. | |||
* [https://finnstats.com/index.php/2021/07/24/how-to-calculate-phi-coefficient-in-r/ How to Calculate Phi Coefficient in R]. It is a measurement of the degree of association between two binary variables. | |||
<li>[https://en.wikipedia.org/wiki/Cram%C3%A9r%27s_V Cramér’s V]. Its value is [0, 1]. A value of zero indicates that there is no association between the two variables. This means that knowing the value of one variable does not help predict the value of the other variable. | |||
* [https://www.statology.org/interpret-cramers-v/ How to Interpret Cramer’s V (With Examples)] | |||
<pre> | |||
library(vcd) | |||
cramersV <- assocstats(table(x, y))$cramer | |||
</pre> | |||
</ul> | |||
== Coefficient of variation (CV) == | == Coefficient of variation (CV) == | ||
[https://en.wikipedia.org/wiki/Coefficient_of_variation Coefficient of variation] | |||
Motivating the coefficient of variation (CV) for beginners: | Motivating the coefficient of variation (CV) for beginners: | ||
| Line 43: | Line 64: | ||
== Agreement == | == Agreement == | ||
=== Pitfalls === | |||
[https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5654219/ Common pitfalls in statistical analysis: Measures of agreement] 2017 | [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5654219/ Common pitfalls in statistical analysis: Measures of agreement] 2017 | ||
| Line 68: | Line 91: | ||
== Computing different kinds of correlations == | == Computing different kinds of correlations == | ||
[https://github.com/easystats/correlation correlation] package | [https://github.com/easystats/correlation correlation] package | ||
=== Partial correlation === | |||
[https://en.wikipedia.org/wiki/Partial_correlation Partial correlation] | |||
== Association is not causation == | |||
* [https://rafalab.github.io/dsbook/association-is-not-causation.html Association is not causation] | |||
* [https://www.r-bloggers.com/2025/06/correlation-vs-causation-understanding-the-difference/ Correlation vs Causation: Understanding the Difference] | |||
* [https://www.statology.org/correlation-does-not-imply-causation-examples/ Correlation Does Not Imply Causation: 5 Real-World Examples] | |||
* [https://www.r-bloggers.com/2025/09/spurious-correlations-in-r-correlation-is-not-causation/ Spurious Correlations in R – Correlation is not Causation] | |||
* Reasons Why Correlation Does Not Imply Causation | |||
** Third-Variable Problem: There may be an unseen third variable that is influencing both correlated variables. For example, ice cream sales and drowning incidents might be correlated because both increase during the summer, but neither causes the other. | |||
** Reverse Causation: The direction of cause and effect might be opposite to what we assume. For example, one might assume that stress causes poor health (which it can), but it’s also possible that poor health increases stress. | |||
** Coincidence: Sometimes, correlations occur purely by chance, especially if the sample size is large or if many variables are tested. | |||
** Complex Interactions: The relationship between variables can be influenced by a complex interplay of multiple factors that correlation alone cannot unpack. | |||
* Examples | |||
** Example of Correlation without Causation: There is a correlation between the number of fire trucks at a fire scene and the amount of damage caused by the fire. However, this does not mean that the fire trucks cause the damage; rather, larger fires both require more fire trucks and cause more damage. | |||
** Example of Potential Misinterpretation: Studies might find a correlation between coffee consumption and heart disease. Without further investigation, one might mistakenly conclude that drinking coffee causes heart disease. However, it could be that people who drink a lot of coffee are more likely to smoke, and smoking is the actual cause of heart disease. | |||
* [https://lifehacker.com/entertainment/what-people-are-getting-wrong-this-week-correlation-and-causation What People Are Getting Wrong This Week (and Every Week): Correlation and Causation] | |||
== Predictive power score == | == Predictive power score == | ||
| Line 74: | Line 116: | ||
== Transform sample values to their percentiles == | == Transform sample values to their percentiles == | ||
<ul> | |||
<li>[https://stat.ethz.ch/R-manual/R-devel/library/stats/html/ecdf.html ecdf()] | |||
<li>[https://stat.ethz.ch/R-manual/R-devel/library/stats/html/quantile.html quantile()] | |||
* An [https://github.com/cran/TreatmentSelection/blob/master/R/evaluate.trtsel.R example] from the TreatmentSelection package where "type = 1" was used. | |||
{{Pre}} | {{Pre}} | ||
R> x <- c(1,2,3,4,4.5,6,7) | R> x <- c(1,2,3,4,4.5,6,7) | ||
| Line 94: | Line 137: | ||
14.28571% 28.57143% 42.85714% 57.14286% 71.42857% 85.71429% 100% | 14.28571% 28.57143% 42.85714% 57.14286% 71.42857% 85.71429% 100% | ||
1.0 2.0 3.0 4.0 4.5 6.0 7.0 | 1.0 2.0 3.0 4.0 4.5 6.0 7.0 | ||
R> x <- c(2, 6, 8, 10, 20) | |||
R> Fn <- ecdf(x) | |||
R> Fn(x) | |||
[1] 0.2 0.4 0.6 0.8 1.0 | |||
</pre> | </pre> | ||
<li>[https://www.thoughtco.com/what-is-a-percentile-3126238 Definition of a Percentile in Statistics and How to Calculate It] | |||
<li>https://en.wikipedia.org/wiki/Percentile | |||
<li>[https://www.statology.org/percentile-vs-quartile-vs-quantile/ Percentile vs. Quartile vs. Quantile: What’s the Difference?] | |||
* Percentiles: Range from 0 to 100. | |||
* Quartiles: Range from 0 to 4. | |||
* Quantiles: Range from any value to any other value. | |||
</ul> | |||
== Standardization == | == Standardization == | ||
| Line 105: | Line 160: | ||
https://vincentarelbundock.github.io/Rdatasets/ | https://vincentarelbundock.github.io/Rdatasets/ | ||
= Box(Box | == Data and global == | ||
* Age Structure from [https://ourworldindata.org/age-structure One Data in World]. '''Our World in Data''' is a non-profit organization that provides free and open access to data and insights on how the world is changing across 115 topics. | |||
= Box(Box, whisker & outlier) = | |||
* https://en.wikipedia.org/wiki/Box_plot, [https://en.wikipedia.org/wiki/Box_plot#/media/File:Boxplot_vs_PDF.svg Boxplot and a probability density function (pdf) of a Normal Population] for a good annotation. | * https://en.wikipedia.org/wiki/Box_plot, [https://en.wikipedia.org/wiki/Box_plot#/media/File:Boxplot_vs_PDF.svg Boxplot and a probability density function (pdf) of a Normal Population] for a good annotation. | ||
* https://owi.usgs.gov/blog/boxplots/ (ggplot2 is used, graph-assisting explanation) | * https://owi.usgs.gov/blog/boxplots/ (ggplot2 is used, graph-assisting explanation) | ||
* https://flowingdata.com/2008/02/15/how-to-read-and-use-a-box-and-whisker-plot/ | * https://flowingdata.com/2008/02/15/how-to-read-and-use-a-box-and-whisker-plot/ | ||
* [https://en.wikipedia.org/wiki/Quartile Quartile] from Wikipedia. The quartiles returned from R are the same as the method defined by Method 2 described in Wikipedia. | * [https://en.wikipedia.org/wiki/Quartile Quartile] from Wikipedia. The quartiles returned from R are the same as the method defined by Method 2 described in Wikipedia. | ||
* [https://www.rforecology.com/post/2022-04-06-how-to-make-a-boxplot-in-r/ How to make a boxplot in R]. The '''whiskers''' of a box and whisker plot are the dotted lines outside of the grey box. These end at the minimum and maximum values of your data set, '''excluding outliers'''. | |||
An example for a graphical explanation. [[:File:Boxplot.svg]], [[:File:Geom boxplot.png]] | An example for a graphical explanation. [[:File:Boxplot.svg]], [[:File:Geom boxplot.png]] | ||
| Line 142: | Line 201: | ||
** Note that ''the cutoffs are not shown in the Box plot''. | ** Note that ''the cutoffs are not shown in the Box plot''. | ||
* Whisker (defined using the cutoffs used to define outliers) | * Whisker (defined using the cutoffs used to define outliers) | ||
** '''Upper whisker''' is defined by '''the largest "data" below 3rd quartile + 1.5 * IQR''' (8 in this example) | ** '''Upper whisker''' is defined by '''the largest "data" below 3rd quartile + 1.5 * IQR''' (8 in this example). Note Upper whisker is NOT defined as 3rd quartile + 1.5 * IQR. | ||
** '''Lower whisker''' is defined by '''the smallest "data" greater than 1st quartile - 1.5 * IQR''' (0 in this example). | ** '''Lower whisker''' is defined by '''the smallest "data" greater than 1st quartile - 1.5 * IQR''' (0 in this example). Note lower whisker is NOT defined as 1st quartile - 1.5 * IQR. | ||
** See another example below where we can see the whiskers fall on observations. | ** See another example below where we can see the whiskers fall on observations. | ||
* Some software like GraphPad has multiple ways to draw whiskers, e.g., 5 and 95 percentiles. See [https://www.graphpad.com/support/faq/five-ways-to-plot-whiskers-in-box-and-whisker-plots/ Five ways to plot whiskers in box and whisker plots]. | |||
Note the [http://en.wikipedia.org/wiki/Box_plot wikipedia] lists several possible definitions of a whisker. R uses the 2nd method (Tukey boxplot) to define whiskers. | Note the [http://en.wikipedia.org/wiki/Box_plot wikipedia] lists several possible definitions of a whisker. R uses the 2nd method (Tukey boxplot) to define whiskers. | ||
| Line 202: | Line 262: | ||
== Annotated boxplot == | == Annotated boxplot == | ||
https://stackoverflow.com/a/38032281 | https://stackoverflow.com/a/38032281 | ||
== Outliers in data analysis == | |||
[https://www.r-bloggers.com/2025/12/outliers-in-data-analysis-detecting-extreme-values-before-modeling-in-r-with-istanbul-airbnb-data/ Outliers in Data Analysis: Detecting Extreme Values Before Modeling in R with İstanbul Airbnb Data] | |||
= stem and leaf plot = | = stem and leaf plot = | ||
| Line 264: | Line 327: | ||
* [https://en.wikipedia.org/wiki/Power_transform#Box%E2%80%93Cox_transformation Power transformation] | * [https://en.wikipedia.org/wiki/Power_transform#Box%E2%80%93Cox_transformation Power transformation] | ||
* [http://denishaine.wordpress.com/2013/03/11/veterinary-epidemiologic-research-linear-regression-part-3-box-cox-and-matrix-representation/ Finding transformation for normal distribution] | * [http://denishaine.wordpress.com/2013/03/11/veterinary-epidemiologic-research-linear-regression-part-3-box-cox-and-matrix-representation/ Finding transformation for normal distribution] | ||
= CLT/Central limit theorem = | |||
[https://en.wikipedia.org/wiki/Central_limit_theorem Central limit theorem] | |||
== Delta method == | |||
[[Delta|Delta]] | |||
== Sample median, x-percentiles == | |||
<ul> | |||
<li>[https://stats.stackexchange.com/questions/45124/central-limit-theorem-for-sample-medians Central limit theorem for sample medians] | |||
<li>For the q-th sample quantile in sufficiently large samples, we get that it will approximately have a normal distribution with mean the <math>𝑞</math>th population quantile <math>𝑥_𝑞</math> and variance <math>𝑞(1−𝑞)/(𝑛𝑓_𝑋(𝑥_𝑞)^2)</math>. | |||
Hence for the '''median''' (𝑞=1/2), the variance in sufficiently large samples will be approximately <math>1/(4𝑛𝑓_𝑋(m)^2)</math>. | |||
<li>For example for an exponential distribution with a rate parameter <math>\lambda >0</math>, the pdf is <math>f(x)=\lambda \exp(-\lambda x)</math>. The population median <math>m</math> is the value such as <math>F(m)=.5</math>. So <math>m=log(2)/\lambda</math>. For large n, the '''sample median''' <math>\tilde{X}</math> will be approximately normal distributed around the population median <math>m</math>, but with the asymptotic variance given by <math>Var(\tilde{X}) \approx \frac{1}{4nf(m)^2} </math> where <math>f(m)</math> is the PDF evaluated at the median <math>m=\log(2)/\lambda</math>. For the exponential distribution with rate <math>\lambda</math>, we have <math>f(m) = \lambda e^{-\lambda m} = \lambda/2</math>. Substituting this into the expression for the variance we have <math>Var(\tilde{X}) \approx \frac{1}{n\lambda^2} </math>. | |||
<li>For normal distribution with mean <math>\mu</math> and variance <math>\sigma^2</math>. The '''sample median''' has a limiting distribution of normal with mean <math>\mu</math> and variance <math> \frac{1}{4nf(m)^2} = \frac{\pi \sigma^2}{2n} </math>. | |||
<li>Some references: | |||
* "Mathematical Statistics" by Jun Shao | |||
* "Probability and Statistics" by DeGroot and Schervish | |||
* "Order Statistics" by H.A. David and H.N. Nagaraja | |||
</ul> | |||
= the Holy Trinity (LRT, Wald, Score tests) = | = the Holy Trinity (LRT, Wald, Score tests) = | ||
| Line 270: | Line 356: | ||
* [http://www.tandfonline.com/doi/full/10.1080/00031305.2014.955212#abstract?ai=rv&mi=3be122&af=R The “Three Plus One” Likelihood-Based Test Statistics: Unified Geometrical and Graphical Interpretations] | * [http://www.tandfonline.com/doi/full/10.1080/00031305.2014.955212#abstract?ai=rv&mi=3be122&af=R The “Three Plus One” Likelihood-Based Test Statistics: Unified Geometrical and Graphical Interpretations] | ||
* [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5969114/ Variable selection – A review and recommendations for the practicing statistician] by Heinze et al 2018. | * [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5969114/ Variable selection – A review and recommendations for the practicing statistician] by Heinze et al 2018. | ||
** Score test is step-up. Score test is typically used in forward steps to screen covariates currently not included in a model for their ability to improve model. | ** [https://en.wikipedia.org/wiki/Score_test '''Score test'''] is step-up. Score test is typically used in forward steps to screen covariates currently not included in a model for their ability to improve model. | ||
** Wald test is step-down. Wald test starts at the full model. It evaluate the significance of a variable by comparing the ratio of its estimate and its standard error with an appropriate | ** [https://en.wikipedia.org/wiki/Wald_test '''Wald test'''] is step-down. Wald test starts at the full model. It evaluate the significance of a variable by comparing the ratio of its estimate and its standard error with an appropriate '''T distribution (for linear models)''' or '''standard normal distribution (for logistic or Cox regression)'''. | ||
** Likelihood ratio tests provide the best control over nuisance parameters by maximizing the likelihood over them both in H0 model and H1 model. In particular, if several coefficients are being tested simultaneously, LRTs for model comparison are preferred over Wald or score tests. | ** [https://en.wikipedia.org/wiki/Likelihood-ratio_test '''Likelihood ratio tests'''] provide the best control over nuisance parameters by maximizing the likelihood over them both in H0 model and H1 model. In particular, if several coefficients are being tested simultaneously, LRTs for model comparison are preferred over Wald or score tests. | ||
* R packages | * R packages | ||
** lmtest package, [https://www.rdocumentation.org/packages/lmtest/versions/0.9-37/topics/waldtest waldtest()] and [https://www.rdocumentation.org/packages/lmtest/versions/0.9-37/topics/lrtest lrtest()]. [https://finnstats.com/index.php/2021/11/24/likelihood-ratio-test-in-r/ Likelihood Ratio Test in R with Example] | ** [https://cran.r-project.org/web/packages/lmtest/ lmtest] package, [https://www.rdocumentation.org/packages/lmtest/versions/0.9-37/topics/waldtest waldtest()] and [https://www.rdocumentation.org/packages/lmtest/versions/0.9-37/topics/lrtest lrtest()]. [https://finnstats.com/index.php/2021/11/24/likelihood-ratio-test-in-r/ Likelihood Ratio Test in R with Example] | ||
** [https://cran.r-project.org/web/packages/aod/index.html aod] package. [https://www.statology.org/wald-test-in-r/ How to Perform a Wald Test in R] | |||
** [https://cran.r-project.org/web/packages/survey/index.html survey] package. regTermTest() | |||
** [https://cran.r-project.org/web/packages/nlWaldTest/index.html nlWaldTest] package. | |||
* [https://stats.stackexchange.com/a/503720 Likelihood ratio test multiplying by 2]. Hint: Approximate the log-likelihood for the '''true value of the parameter''' using the Taylor expansion around the '''MLE'''. | |||
* Wald statistic relationship to Z-statistic: The Wald statistic is essentially the square of the Z-statistic. In other words, a Wald statistic is computed as Z squared. However, '''there is a key difference in the denominator of these statistics: the Z-statistic uses the null standard error (calculated using the hypothesized value), while the Wald statistic uses the standard error evaluated at the maximum likelihood estimate'''. | |||
** [https://stats.stackexchange.com/questions/60074/wald-test-for-logistic-regression Wald test for logistic regression] | |||
** [https://stats.stackexchange.com/questions/152630/wald-test-and-z-test Wald Test and Z Test] | |||
** [https://stats.stackexchange.com/questions/609613/what-is-the-difference-between-z-value-and-the-wald-statistic-in-the-summary-fun What is the difference between z-value and the Wald statistic in the summary function of the Cox Proportional Hazards model of the “survival” package?] | |||
= Don't invert that matrix = | = Don't invert that matrix = | ||
| Line 325: | Line 422: | ||
* [https://www.statworx.com/de/blog/simulating-the-bias-variance-tradeoff-in-r/ Simulating the bias-variance tradeoff in R] | * [https://www.statworx.com/de/blog/simulating-the-bias-variance-tradeoff-in-r/ Simulating the bias-variance tradeoff in R] | ||
* [https://alemorales.info/post/variance-estimators/ Estimating variance: should I use n or n - 1? The answer is not what you think] | * [https://alemorales.info/post/variance-estimators/ Estimating variance: should I use n or n - 1? The answer is not what you think] | ||
== Brier score == | |||
* https://en.wikipedia.org/wiki/Brier_score (it was proposed by Glenn W. Brier in 1950) | |||
* It seems Brier Score and Mean Squared error have the same formula. | |||
* Brier score seems to be applied to binary or category outcome (prediction is probabilities in [0,1]) while mean squared error is applied to continuous value outcome (prediction is numeric values). | |||
== Splines == | == Splines == | ||
| Line 334: | Line 436: | ||
== k-Nearest neighbor regression == | == k-Nearest neighbor regression == | ||
* [https://www.rdocumentation.org/packages/class/versions/7.3-21/topics/knn class::knn()] | |||
* k-NN regression in practice: boundary problem, discontinuities problem. | * k-NN regression in practice: boundary problem, discontinuities problem. | ||
* Weighted k-NN regression: want weight to be small when distance is large. Common choices - weight = kernel(xi, x) | * Weighted k-NN regression: want weight to be small when distance is large. Common choices - weight = kernel(xi, x) | ||
| Line 347: | Line 450: | ||
See [[PCA|PCA]]. | See [[PCA|PCA]]. | ||
= Partial Least Squares (PLS) = | = Partial Least Squares (PLS) regression = | ||
<ul> | |||
<li>[https://twitter.com/slavov_n/status/1642570040737402881 Accounting for measurement errors with total least squares]. Demonstrate the bias of the PLS. | |||
<li>https://en.wikipedia.org/wiki/Partial_least_squares_regression. The general underlying model of multivariate PLS is | |||
:<math>X = T P^\mathrm{T} + E</math> | :<math>X = T P^\mathrm{T} + E</math> | ||
:<math>Y = U Q^\mathrm{T} + F</math> | :<math>Y = U Q^\mathrm{T} + F</math> | ||
where {{mvar|X}} is an <math>n \times m</math> matrix of predictors, {{mvar|Y}} is an <math>n \times p</math> matrix of responses; {{mvar|T}} and {{mvar|U}} are <math>n \times l</math> matrices that are, respectively, '''projections''' of {{mvar|X}} (the X '''score''', ''component'' or '''factor matrix''') and projections of {{mvar|Y}} (the ''Y scores''); {{mvar|P}} and {{mvar|Q}} are, respectively, <math>m \times l</math> and <math>p \times l</math> orthogonal '''loading matrices'''; and matrices {{mvar|E}} and {{mvar|F}} are the error terms, assumed to be independent and identically distributed random normal variables. The decompositions of {{mvar|X}} and {{mvar|Y}} are made so as to maximise the '''covariance''' between {{mvar|T}} and {{mvar|U}} (projection matrices). | :where {{mvar|X}} is an <math>n \times m</math> matrix of predictors, {{mvar|Y}} is an <math>n \times p</math> matrix of responses; {{mvar|T}} and {{mvar|U}} are <math>n \times l</math> matrices that are, respectively, '''projections''' of {{mvar|X}} (the X '''score''', ''component'' or '''factor matrix''') and projections of {{mvar|Y}} (the ''Y scores''); {{mvar|P}} and {{mvar|Q}} are, respectively, <math>m \times l</math> and <math>p \times l</math> orthogonal '''loading matrices'''; and matrices {{mvar|E}} and {{mvar|F}} are the error terms, assumed to be independent and identically distributed random normal variables. The decompositions of {{mvar|X}} and {{mvar|Y}} are made so as to maximise the '''covariance''' between {{mvar|T}} and {{mvar|U}} (projection matrices). | ||
<li>[https://www.gokhanciflikli.com/post/learning-brexit/ Supervised vs. Unsupervised Learning: Exploring Brexit with PLS and PCA] | |||
<li>[https://cran.r-project.org/web/packages/pls/index.html pls] R package | |||
<li>[https://cran.r-project.org/web/packages/plsRcox/index.html plsRcox] R package (archived). See [[R#install_a_tar.gz_.28e.g._an_archived_package.29_from_a_local_directory|here]] for the installation. | |||
<li>[https://web.stanford.edu/~hastie/ElemStatLearn//printings/ESLII_print12.pdf#page=101 PLS, PCR (principal components regression) and ridge regression tend to behave similarly]. Ridge regression may be preferred because it shrinks smoothly, rather than in discrete steps. | |||
<li>[https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-019-3310-7 So you think you can PLS-DA?]. Compare PLS with PCA. | |||
<li>[https://cran.r-project.org/web/packages/plsRglm/index.html plsRglm] package - Partial Least Squares Regression for Generalized Linear Models | |||
</ul> | |||
== Partial Least Squares Discriminant Analysis (PLS-DA) == | |||
<ul> | |||
<li>Partial least squares discriminant analysis (PLS-DA) is a variant used when the Y is categorical. | |||
<li>[https://bioconductor.org/packages/release/bioc/vignettes/mixOmics/inst/doc/vignette.html mixOmics] package. | |||
<li>Application: [https://jneuroinflammation.biomedcentral.com/articles/10.1186/s12974-024-03218-0 Comprehensive analysis of the cerebrospinal fluid and serum metabolome in neurological diseases]. | |||
</ul> | |||
= High dimension = | = High dimension = | ||
| Line 380: | Line 494: | ||
== ICS vs FA == | == ICS vs FA == | ||
== Robust independent component analysis == | |||
[https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-022-05043-9 robustica: customizable robust independent component analysis] 2022 | |||
= Canonical correlation analysis = | = Canonical correlation analysis = | ||
| Line 386: | Line 503: | ||
* [https://online.stat.psu.edu/stat505/book/export/html/682 Canonical Correlation Analysis] from psu.edu | * [https://online.stat.psu.edu/stat505/book/export/html/682 Canonical Correlation Analysis] from psu.edu | ||
* see the [https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/cancor cancor] function in base R; canocor in the [https://cran.r-project.org/web/packages/calibrate/ calibrate] package; and the [https://cran.r-project.org/web/packages/CCA/index.html CCA] package. | * see the [https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/cancor cancor] function in base R; canocor in the [https://cran.r-project.org/web/packages/calibrate/ calibrate] package; and the [https://cran.r-project.org/web/packages/CCA/index.html CCA] package. | ||
* [https://cmdlinetips.com/2020/12/canonical-correlation-analysis-in-r/ Introduction to Canonical Correlation Analysis (CCA) in R] | |||
== Non-negative CCA == | |||
* https://cran.r-project.org/web/packages/nscancor/ | |||
* [https://www.mdpi.com/2076-3417/12/13/6596/html Pan-Cancer Analysis for Immune Cell Infiltration and Mutational Signatures Using Non-Negative Canonical Correlation Analysis] 2022. Non-negative constraints that force all input elements and coefficients to be zero or positive values. | |||
= [https://en.wikipedia.org/wiki/Correspondence_analysis Correspondence analysis] = | = [https://en.wikipedia.org/wiki/Correspondence_analysis Correspondence analysis] = | ||
| Line 397: | Line 519: | ||
= Nonlinear dimension reduction = | = Nonlinear dimension reduction = | ||
[https://www.biorxiv.org/content/10.1101/2021.08.25.457696v1 The Specious Art of Single-Cell Genomics] by Chari 2021 | * [https://www.biorxiv.org/content/10.1101/2021.08.25.457696v1 The Specious Art of Single-Cell Genomics] by Chari 2021 | ||
== polarisR package == | |||
[https://cran.r-project.org/web/packages/polarisR/index.html polarisR]. A 'shiny' application for visualizing high-dimensional data using non-linear dimensionality reduction (NLDR) techniques such as t-SNE and UMAP. It provides an interactive platform to explore high-dimensional datasets, diagnose the quality of the embeddings using the 'quollr' package, and compare different NLDR methods. | |||
== t-SNE == | == t-SNE == | ||
| Line 404: | Line 529: | ||
* [https://en.wikipedia.org/wiki/Nonlinear_dimensionality_reduction#t-distributed_stochastic_neighbor_embedding Wikipedia] | * [https://en.wikipedia.org/wiki/Nonlinear_dimensionality_reduction#t-distributed_stochastic_neighbor_embedding Wikipedia] | ||
* [https://youtu.be/NEaUSP4YerM StatQuest: t-SNE, Clearly Explained] | * [https://youtu.be/NEaUSP4YerM StatQuest: t-SNE, Clearly Explained] | ||
* https://lvdmaaten.github.io/tsne/ | * https://lvdmaaten.github.io/tsne/ | ||
* [https://rpubs.com/Saskia/520216 Workshop: Dimension reduction with R] Saskia Freytag | * [https://rpubs.com/Saskia/520216 Workshop: Dimension reduction with R] Saskia Freytag | ||
| Line 412: | Line 536: | ||
* [https://intobioinformatics.wordpress.com/2019/05/30/quick-and-easy-t-sne-analysis-in-r/ Quick and easy t-SNE analysis in R]. [https://bioconductor.org/packages/devel/bioc/html/M3C.html M3C] package was used. | * [https://intobioinformatics.wordpress.com/2019/05/30/quick-and-easy-t-sne-analysis-in-r/ Quick and easy t-SNE analysis in R]. [https://bioconductor.org/packages/devel/bioc/html/M3C.html M3C] package was used. | ||
* [https://link.springer.com/protocol/10.1007%2F978-1-0716-0301-7_8 Visualization of Single Cell RNA-Seq Data Using t-SNE in R]. [https://cran.r-project.org/web/packages/Seurat/index.html Seurat] (both Seurat and M3C call [https://cran.r-project.org/web/packages/Rtsne/index.html Rtsne]) package was used. | * [https://link.springer.com/protocol/10.1007%2F978-1-0716-0301-7_8 Visualization of Single Cell RNA-Seq Data Using t-SNE in R]. [https://cran.r-project.org/web/packages/Seurat/index.html Seurat] (both Seurat and M3C call [https://cran.r-project.org/web/packages/Rtsne/index.html Rtsne]) package was used. | ||
* [https://github.com/berenslab/rna-seq-tsne The art of using t-SNE for single-cell transcriptomics] | * [https://github.com/berenslab/rna-seq-tsne The art of using t-SNE for single-cell transcriptomics] | ||
* [https://www.frontiersin.org/articles/10.3389/fgene.2020.00041/full Normalization Methods on Single-Cell RNA-seq Data: An Empirical Survey] | * [https://www.frontiersin.org/articles/10.3389/fgene.2020.00041/full Normalization Methods on Single-Cell RNA-seq Data: An Empirical Survey] | ||
| Line 503: | Line 625: | ||
* fashion_mnist is only 500x785 | * fashion_mnist is only 500x785 | ||
* [https://tensorflow.rstudio.com/reference/keras/dataset_fashion_mnist/ keras] has 60k x 785. Miniconda is required when we want to use the package. | * [https://tensorflow.rstudio.com/reference/keras/dataset_fashion_mnist/ keras] has 60k x 785. Miniconda is required when we want to use the package. | ||
=== tSNE vs PCA === | |||
* [https://medium.com/analytics-vidhya/pca-vs-t-sne-17bcd882bf3d PCA vs t-SNE: which one should you use for visualization]. This uses MNIST dataset for a comparison. | |||
* [https://www.subioplatform.com/info_casestudy/338/why-pca-on-bulk-rna-seq-and-t-sne-on-scrna-seq Why PCA on bulk RNA-Seq and t-SNE on scRNA-Seq?] | |||
* [https://support.bioconductor.org/p/97594/ What to use: PCA or tSNE dimension reduction in DESeq2 analysis?] (with discussion) | |||
* [https://stats.stackexchange.com/a/249520 Are there cases where PCA is more suitable than t-SNE?] | |||
* [https://stats.stackexchange.com/a/502392 How to interpret data not separated by PCA but by T-sne/UMAP] | |||
* [https://towardsdatascience.com/dimensionality-reduction-for-data-visualization-pca-vs-tsne-vs-umap-be4aa7b1cb29 Dimensionality Reduction for Data Visualization: PCA vs TSNE vs UMAP vs LDA] | |||
=== Two groups example === | === Two groups example === | ||
| Line 523: | Line 653: | ||
== UMAP == | == UMAP == | ||
<ul> | |||
<li>[https://en.wikipedia.org/wiki/Nonlinear_dimensionality_reduction#Uniform_manifold_approximation_and_projection Uniform manifold approximation and projection] | |||
<li>UMAP creates a low-dimensional map that preserves local similarity relationships in high-dimensional data, allowing humans to visualize complex biological structure without using the map itself for classification or decision-making. | |||
<li>Properties: | |||
[https:// | * Non-linear | ||
* Preserves neighborhood structure/Local structure (vs PCA preserves variance). Points close together → similar profiles. Both UMAP and t-SNE are designed to preserve local structure. | |||
* Stochastic (unless seeded) | |||
* Gaps do not imply real biological distance | |||
* Visual bias: UMAP appears more “continuous” but still distorts space. t-SNE exaggerates separation. | |||
<li>[https://www.geeksforgeeks.org/data-visualization/techniques-for-visualizing-high-dimensional-data/ Techniques for Visualizing High Dimensional Data] | |||
* good at displaying both '''global and local structure'''. | |||
* Because of its '''speed''', it's ideal for big datasets. | |||
* t-sne was invented in 2008 and umap was 2018. | |||
<li>https://cran.r-project.org/web/packages/uwot/index.html (more popular than the umap package) | |||
<ul> | |||
<li>There is no official "backronym" for uwot in the documentation. In the R community, it is generally understood to be a play on the British/internet slang "U wat?" (as in "You what?"). | |||
<li>Install on macOS/Linux requires compilation. | |||
<li>(macOS) First install gfortran by downloading gfortran from https://mac.r-project.org/tools/. The installer said The resulting compiler will live in '''/opt/gfortran''' and can be called with '''/opt/gfortran/bin/gfortran''' You can uninstall this package with '''sudo gfortran-uninstall''' | |||
<li>After installation, in the shell | |||
<pre> | |||
echo 'export PATH="/opt/gfortran/bin:$PATH"' >> ~/.zshrc | |||
source ~/.zshrc | |||
# Verify | |||
echo $PATH | |||
which gfortran | |||
gfortran --version | |||
R CMD config FC | |||
# List any other gfortran on the disk (trouble shooting) | |||
sudo find / -type f -name gfortran -perm -111 -print 2>/dev/null | head -n 200 | |||
* Search by image: graphical explanation of calibration problem | # Install RSpectra | ||
* [https://bmcmedicine.biomedcentral.com/articles/10.1186/s12916-019-1466-7 Calibration: the Achilles heel of predictive analytics] Calster 2019 | export CC=clang | ||
* https://www.itl.nist.gov/div898/handbook/pmd/section1/pmd133.htm Calibration and '''calibration curve'''. | export CXX=clang++ | ||
** Y=voltage (''observed''), X=temperature (''true/ideal''). The calibration curve for a thermocouple is often constructed by comparing thermocouple ''(observed)output'' to relatively ''(true)precise'' thermometer data. | export CXX11=clang++ | ||
R -e 'install.packages("RSpectra", type="source", INSTALL_opts=c("--no-multiarch","--clean","--verbose"))' | |||
R -e 'install.packages("uwot", type="source", INSTALL_opts=c("--no-multiarch","--clean","--verbose"))' | |||
</pre> | |||
<li>[https://cran.r-project.org/web/packages/uwot/refman/uwot.html#umap_transform umap_transform()] - Add New Points to an Existing Embedding.</br> | |||
[[File:Uwot.png|250px]] | |||
</ul> | |||
<li>https://cran.r-project.org/web/packages/umap/index.html | |||
<ul> | |||
<li>Iris example. | |||
* Note by default umap(, preserve.seed = TRUE). When umap() starts, it saves the current state of the '''global R RNG (Random Number Generator)'''. | |||
* The global R Random Number Generator (RNG) state changes whenever you call a function that generates a pseudo-random number. | |||
* It is better to use the '''random_state''' parameter instead of set.seed(). The default value is NA for random_state. | |||
* The default umap parameters are defined in the variable '''umap.defaults''' | |||
[[File:Umap-iris.png|250px]] | |||
<li>[https://www.rdocumentation.org/packages/umap/versions/0.2.10.0/topics/predict.umap predict.umap()] | |||
<pre> | |||
iris.umap = umap::umap(x_train) | |||
perturbed.embedding = predict(iris.umap, x_test) | |||
head(perturbed.embedding) # 11 x 2 | |||
</pre> | |||
</ul> | |||
<li>[https://intobioinformatics.wordpress.com/2019/06/08/running-umap-for-data-visualisation-in-r/ Running UMAP for data visualisation in R] (M3C package) | |||
<li>[https://juliasilge.com/blog/cocktail-recipes-umap/ PCA and UMAP with tidymodels] | |||
<li>[https://arxiv.org/abs/1802.03426 UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction] | |||
<li>https://www.biorxiv.org/content/early/2018/04/10/298430 | |||
<li>[https://poissonisfish.com/2020/11/14/umap-clustering-in-python/ UMAP clustering in Python] | |||
<li>[https://juliasilge.com/blog/un-voting/ Dimensionality reduction of #TidyTuesday United Nations voting patterns], [https://juliasilge.com/blog/billboard-100/ Dimensionality reduction for #TidyTuesday Billboard Top 100 songs]. The [https://cran.r-project.org/web/packages/embed/index.html embed] package was used. | |||
<li>[https://tonyelhabr.rbind.io/post/dimensionality-reduction-and-clustering/ Tired: PCA + kmeans, Wired: UMAP + GMM] | |||
<li>[https://www.nature.com/articles/s41596-020-00409-w Tutorial: guidelines for the computational analysis of single-cell RNA sequencing data] Andrews 2020. | |||
* One shortcoming of both t-SNE and UMAP is that they both require a user-defined hyperparameter, and the result can be sensitive to the value chosen. Moreover, the methods are stochastic, and providing a good initialization can significantly improve the results of both algorithms. | |||
* '''Neither visualization algorithm preserves cell-cell distances, so the resulting embedding should not be used directly by downstream analysis methods such as clustering or pseudotime inference'''. | |||
<li>[https://youtu.be/eN0wFzBA4Sc?t=53 UMAP Dimension Reduction, Main Ideas!!!], [https://youtu.be/jth4kEvJ3P8 UMAP: Mathematical Details (clearly explained!!!)] | |||
<li>[https://towardsdatascience.com/how-exactly-umap-works-13e3040e1668 How Exactly UMAP Works] (open it in an incognito window] | |||
<li>[https://statquest.gumroad.com/l/nixkdy t-SNE and UMAP Study Guide] | |||
<li>[https://twitter.com/lpachter/status/1440696798218100753 UMAP monkey] | |||
<li>[https://simplystatistics.org/posts/2024-12-23-biologists-stop-including-umap-plots-in-your-papers/ Biologists, stop putting UMAP plots in your papers] | |||
<li>[https://www.r-bloggers.com/2025/11/dimension-reduction/ Visualizing French Town Data: UMAP Projection of Location and Population] | |||
</ul> | |||
== Why Inference is Problematic == | |||
UMAP is for Exploration, not Inference | |||
<ul> | |||
<li>UMAP is a '''non-linear projection''' that warps the original space to preserve local neighbors. It makes assumptions about the data (that it lies on a low-dimensional manifold) and uses techniques from topological data analysis to find the best arrangement. | |||
<li>Why Inference is Problematic | |||
{| class="wikitable" | |||
|+ UMAP: Exploration vs. Inference | |||
! Feature | |||
! Statistical Meaning | |||
! Implication for UMAP | |||
|- | |||
| '''Cluster Size''' | |||
| In traditional statistics, a larger cluster implies higher density. | |||
| '''Meaningless.''' UMAP optimizes for ''' 'local connectivity' ''', and the physical size or density of a cluster in the 2D plot is '''not''' proportional to the density in the original high-dimensional space. | |||
|- | |||
| '''Distance Between Clusters''' | |||
| Distance implies a quantitative measure of dissimilarity. | |||
| '''Misleading.''' While UMAP is better than t-SNE at preserving '''global structure''', the '''exact distances''' between clusters (how far apart two groups of points are) are an '''artifact''' of the algorithm and should not be used to infer the actual degree of separation in the original data. | |||
|- | |||
| '''Coordinates (UMAP1, UMAP2)''' | |||
| The axes have a defined, independent physical or statistical meaning (e.g., age, income). | |||
| '''Uninterpretable.''' The UMAP coordinates (`UMAP1`, `UMAP2`, etc.) are arbitrary results of a complex, non-linear mathematical transformation and have '''no direct statistical meaning''' tied to the original features. | |||
|} | |||
</ul> | |||
== GECO == | |||
[https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-020-03951-2 GECO: gene expression clustering optimization app for non-linear data visualization of patterns] | |||
= Visualize the random effects = | |||
http://www.quantumforest.com/2012/11/more-sense-of-random-effects/ | |||
= [https://en.wikipedia.org/wiki/Calibration_(statistics) Calibration] = | |||
* Search by image: graphical explanation of calibration problem | |||
* Does calibrating classification models improve prediction? | |||
** Calibrating a classification model can improve the reliability and accuracy of the '''predicted probabilities''', but it may not necessarily improve the '''overall prediction performance of the model''' in terms of metrics such as accuracy, precision, or recall. | |||
** Calibration is about ensuring that the predicted probabilities from a model match the observed proportions of outcomes in the data. This can be important when the predicted probabilities are used to make decisions or when they are presented to users as a measure of confidence or uncertainty. | |||
** However, calibrating a model does not change its ability to discriminate between positive and negative outcomes. In other words, calibration does not affect how well the model separates the classes, but rather how accurately it estimates the probabilities of class membership. | |||
** In some cases, calibrating a model may improve its overall prediction performance by making the predicted probabilities more accurate. However, this is not always the case, and the impact of calibration on prediction performance may vary depending on the specific needs and goals of the analysis. | |||
* A real-world example of calibration in machine learning is in the field of fraud detection. In this case, it might be desirable to have the model '''predict probabilities''' of data belonging to each possible '''class''' instead of crude class labels. Gaining access to '''probabilities''' is useful for a richer interpretation of the responses, analyzing the model shortcomings, or presenting the uncertainty to the end-users ². [https://wttech.blog/blog/2021/a-guide-to-model-calibration/ A guide to model calibration | Wunderman Thompson Technology]. | |||
* Another example where calibration is more important than prediction on new samples is in the field of medical diagnosis. In this case, it is important to have well-calibrated probabilities for the presence of a disease, so that doctors can make informed decisions about treatment. For example, if a diagnostic test predicts an 80% chance that a patient has a certain disease, doctors would expect that 80% of the time when such a prediction is made, the patient actually has the disease. This example does not mean that prediction on new samples is not feasible or not a concern, but rather that having well-calibrated probabilities is crucial for making accurate predictions and informed decisions. | |||
* [https://bmcmedicine.biomedcentral.com/articles/10.1186/s12916-019-1466-7 Calibration: the Achilles heel of predictive analytics] Calster 2019 | |||
* https://www.itl.nist.gov/div898/handbook/pmd/section1/pmd133.htm Calibration and '''calibration curve'''. | |||
** Y=voltage (''observed''), X=temperature (''true/ideal''). The calibration curve for a thermocouple is often constructed by comparing thermocouple ''(observed)output'' to relatively ''(true)precise'' thermometer data. | |||
** when a new temperature is measured with the thermocouple, the voltage is converted to temperature terms by plugging the observed voltage into the regression equation and solving for temperature. | ** when a new temperature is measured with the thermocouple, the voltage is converted to temperature terms by plugging the observed voltage into the regression equation and solving for temperature. | ||
** It is important to note that the thermocouple measurements, made on the ''secondary measurement scale'', are treated as the response variable and the more precise thermometer results, on the ''primary scale'', are treated as the predictor variable because this best satisfies the '''underlying assumptions''' (Y=observed, X=true) of the analysis. | ** It is important to note that the thermocouple measurements, made on the ''secondary measurement scale'', are treated as the response variable and the more precise thermometer results, on the ''primary scale'', are treated as the predictor variable because this best satisfies the '''underlying assumptions''' (Y=observed, X=true) of the analysis. | ||
| Line 631: | Line 863: | ||
== Link function == | == Link function == | ||
[http://www.win-vector.com/blog/2019/07/link-functions-versus-data-transforms/ Link Functions versus Data Transforms] | [http://www.win-vector.com/blog/2019/07/link-functions-versus-data-transforms/ Link Functions versus Data Transforms] | ||
== Extract coefficients, z, p-values == | |||
Use '''coef(summary(glmObject))''' | |||
<pre> | |||
> coef(summary(glm.D93)) | |||
Estimate Std. Error z value Pr(>|z|) | |||
(Intercept) 3.044522e+00 0.1708987 1.781478e+01 5.426767e-71 | |||
outcome2 -4.542553e-01 0.2021708 -2.246889e+00 2.464711e-02 | |||
outcome3 -2.929871e-01 0.1927423 -1.520097e+00 1.284865e-01 | |||
treatment2 1.337909e-15 0.2000000 6.689547e-15 1.000000e+00 | |||
treatment3 1.421085e-15 0.2000000 7.105427e-15 1.000000e+00 | |||
</pre> | |||
== Quasi Likelihood == | == Quasi Likelihood == | ||
| Line 654: | Line 898: | ||
* Likelihood ratio tests and the deviance http://data.princeton.edu/wws509/notes/a2.pdf#page=6 | * Likelihood ratio tests and the deviance http://data.princeton.edu/wws509/notes/a2.pdf#page=6 | ||
* Deviance(y,muhat) = 2*(loglik_saturated - loglik_proposed) | * Deviance(y,muhat) = 2*(loglik_saturated - loglik_proposed) | ||
* [http://r.qcbs.ca/workshop06/book-en/binomial-glm.html Binomial GLM] and the [https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/ls objects()] function that seems to be the same as str(, max=1). | |||
* [https://stats.stackexchange.com/questions/108995/interpreting-residual-and-null-deviance-in-glm-r Interpreting Residual and Null Deviance in GLM R] | * [https://stats.stackexchange.com/questions/108995/interpreting-residual-and-null-deviance-in-glm-r Interpreting Residual and Null Deviance in GLM R] | ||
** Null Deviance = 2(LL(Saturated Model) - LL(Null Model)) on df = df_Sat - df_Null. The '''null deviance''' shows how well the response variable is predicted by a model that includes only the intercept (grand mean). | ** Null Deviance = 2(LL(Saturated Model) - LL(Null Model)) on df = df_Sat - df_Null. The '''null deviance''' shows how well the response variable is predicted by a model that includes only the intercept (grand mean). | ||
| Line 725: | Line 970: | ||
* [https://www.seascapemodels.org/rstats/2021/03/27/common-GAM-problems.html How to solve common problems with GAMs] | * [https://www.seascapemodels.org/rstats/2021/03/27/common-GAM-problems.html How to solve common problems with GAMs] | ||
* [https://www.mzes.uni-mannheim.de/socialsciencedatalab/article/gam/ Generalized Additive Models: Allowing for some wiggle room in your models] | * [https://www.mzes.uni-mannheim.de/socialsciencedatalab/article/gam/ Generalized Additive Models: Allowing for some wiggle room in your models] | ||
* [https://www.rdatagen.net/post/2022-08-09-simulating-data-from-a-non-linear-function-by-specifying-some-points-on-the-curve/ Simulating data from a non-linear function by specifying a handful of points] | |||
* [https://www.rdatagen.net/post/2022-11-01-modeling-secular-trend-in-crt-using-gam/ Modeling the secular trend in a cluster randomized trial using very flexible models] | |||
=== Penalty === | |||
[https://www.kenkoonwong.com/blog/gam-penalty/ From Math to Code: Building GAM with Penalty Functions From Scratch] | |||
= Simulate data = | = Simulate data = | ||
| Line 753: | Line 1,003: | ||
== Correlated data == | == Correlated data == | ||
[https://predictivehacks.com/how-to-generate-correlated-data-in-r/ How To Generate Correlated Data In R] | <ul> | ||
<li> [https://predictivehacks.com/how-to-generate-correlated-data-in-r/ How To Generate Correlated Data In R] | |||
<li> [https://www.r-bloggers.com/2023/02/flexible-correlation-generation-an-update-to-gencormat-in-simstudy/ Flexible correlation generation: an update to genCorMat in simstudy] | |||
<li> [https://en.wikipedia.org/wiki/Cholesky_decomposition#Monte_Carlo_simulation Cholesky decomposition] | |||
<pre> | |||
set.seed(1) | |||
n <- 1000 | |||
R <- matrix(c(1, 0.75, 0.75, 1), nrow=2) | |||
M <- matrix(rnorm(2 * n), ncol=2) | |||
M <- M %*% chol(R) # chol(R) is an upper triangular matrix | |||
x <- M[, 1] # First correlated vector | |||
y <- M[, 2] | |||
cor(x, y) | |||
# 0.7502607 | |||
</pre> | |||
<li>[http://cran.r-project.org/web/packages/GenOrd/index.html GenOrd]: Generate ordinal and discrete variables with given correlation matrix and marginal distributions, | |||
[http://statistical-research.com/simulating-random-multivariate-correlated-data-categorical-variables/ here] | |||
</ul> | |||
== Clustered data with marginal correlations == | |||
[https://www.rdatagen.net/post/2022-11-22-generating-cluster-data-with-marginal-correlations/ Generating clustered data with marginal correlations] | |||
== Signal to noise ratio/SNR == | == Signal to noise ratio/SNR == | ||
* https://en.wikipedia.org/wiki/Signal-to-noise_ratio | * https://en.wikipedia.org/wiki/Signal-to-noise_ratio | ||
* https://stats.stackexchange.com/questions/31158/how-to-simulate-signal-noise-ratio | * https://stats.stackexchange.com/questions/31158/how-to-simulate-signal-noise-ratio | ||
: <math>\frac{\sigma^2_{signal}}{\sigma^2_{noise}} = \frac{Var(f(X))}{Var(e)} </math> if Y = f(X) + e | : <math>SNR = \frac{\sigma^2_{signal}}{\sigma^2_{noise}} = \frac{Var(f(X))}{Var(e)} </math> if Y = f(X) + e | ||
* The SNR is related to the correlation of Y and f(X). Assume X and e are independent (<math>X \perp e </math>): | |||
: <math> | |||
\begin{align} | |||
Cor(Y, f(X)) &= Cor(f(X)+e, f(X)) \\ | |||
&= \frac{Cov(f(X)+e, f(X))}{\sqrt{Var(f(X)+e) Var(f(X))}} \\ | |||
&= \frac{Var(f(X))}{\sqrt{Var(f(X)+e) Var(f(X))}} \\ | |||
&= \frac{\sqrt{Var(f(X))}}{\sqrt{Var(f(X)) + Var(e))}} = \frac{\sqrt{SNR}}{\sqrt{SNR + 1}} \\ | |||
&= \frac{1}{\sqrt{1 + Var(e)/Var(f(X))}} = \frac{1}{\sqrt{1 + SNR^{-1}}} | |||
\end{align} | |||
</math> [[File:SnrVScor.png|200px]] | |||
: Or <math>SNR = \frac{Cor^2}{1-Cor^2} </math> | |||
* Page 401 of ESLII (https://web.stanford.edu/~hastie/ElemStatLearn//) 12th print. | * Page 401 of ESLII (https://web.stanford.edu/~hastie/ElemStatLearn//) 12th print. | ||
| Line 768: | Line 1,049: | ||
== Effect size, Cohen's d and volcano plot == | == Effect size, Cohen's d and volcano plot == | ||
<ul> | |||
<li>https://en.wikipedia.org/wiki/Effect_size (See also the estimation by the [[#Two_sample_test_assuming_equal_variance|pooled sd]]) | |||
: <math>\theta = \frac{\mu_1 - \mu_2} \sigma,</math> | : <math>\theta = \frac{\mu_1 - \mu_2} \sigma,</math> | ||
<li>[https://learningstatisticswithr.com/book/hypothesistesting.html#effectsize Effect size, sample size and power] from ebook '''[https://learningstatisticswithr.com/book/ Learning statistics with R]''': A tutorial for psychology students and other beginners. | |||
<li>[https://en.wikipedia.org/wiki/Effect_size#t-test_for_mean_difference_between_two_independent_groups t-statistic and Cohen's d] for the case of mean difference between two independent groups | |||
<li>[http://www.win-vector.com/blog/2019/06/cohens-d-for-experimental-planning/ Cohen’s D for Experimental Planning] | |||
<li>Common Effect Size Measures: | |||
{| class="wikitable" | |||
|+ Common Effect Size Measures | |||
! Type of Analysis !! Effect Size Measure !! Interpretation | |||
|- | |||
| Mean Comparison (t-test, ANOVA) || Cohen’s d || Difference in standard deviation units | |||
|- | |||
| Regression || Standardized β (beta) || Strength of predictor variables | |||
|- | |||
| Correlation || Pearson’s r || Strength & direction of relationship (-1 to 1) | |||
|- | |||
| Categorical Data (Chi-square, Logistic Regression) || Odds Ratio (OR), Risk Ratio (RR) || Strength of association | |||
|} | |||
<li>[https://en.wikipedia.org/wiki/Volcano_plot_(statistics) Volcano plot] | |||
* Y-axis: -log(p) | |||
* X-axis: log2 fold change OR effect size (Cohen's D). [https://twitter.com/biobenkj/status/1072141825568329728 An example] from RNA-Seq data. | |||
<li>Compute Fisher’s Exact Test Power in R. | |||
* The [https://cran.r-project.org/web/packages/Exact/index.html Exact] package. [https://www.rdocumentation.org/packages/Exact/versions/3.3/topics/power.exact.test power.exact.test()] function. | |||
</ul> | |||
== Treatment/control == | |||
* [https://github.com/cran/biospear/blob/master/R/simdata.R simdata()] from [https://cran.r-project.org/web/packages/biospear/index.html biospear] package | |||
* [https://github.com/cran/ROCSI/blob/master/R/ROCSI.R#L598 data.gen()] from [https://cran.r-project.org/web//packages/ROCSI/index.html ROCSI] package. The response contains continuous, binary and survival outcomes. The input include prevalence of predictive biomarkers, effect size (beta) for prognostic biomarker, etc. | |||
== Cauchy distribution has no expectation == | == Cauchy distribution has no expectation == | ||
| Line 785: | Line 1,089: | ||
replicate(10, mean(rcauchy(10000))) | replicate(10, mean(rcauchy(10000))) | ||
</pre> | </pre> | ||
== Dirichlet distribution == | |||
* [https://en.wikipedia.org/wiki/Dirichlet_distribution Dirichlet distribution] | |||
** It is a multivariate generalization of the '''beta''' distribution | |||
** The Dirichlet distribution is the conjugate prior of the categorical distribution and '''multinomial distribution'''. | |||
* [https://cran.r-project.org/web/packages/dirmult/ dirmult]::rdirichlet() | |||
== Relationships among probability distributions == | |||
https://en.wikipedia.org/wiki/Relationships_among_probability_distributions | |||
== What is the probability that two persons have the same initials == | |||
[https://www.r-bloggers.com/2023/12/what-is-the-probability-that-two-persons-have-the-same-initials/ The post]. The probability that at least two persons have the same initials depends on the size of the group. For a team of 8 people, simulations suggest that the probability is close to 4.1%. This probability increases with the size of the group. If there are 1000 people in the room, [https://www.numerade.com/ask/question/whats-the-probability-that-someone-else-in-a-room-full-of-people-has-the-exact-same-3-initials-in-their-name-thats-in-another-persons-name-a-038-b-333-c-0057-d-0064/ the probability is almost 100%]. [https://math.stackexchange.com/a/606272 How many people do you need to guarantee that two of them have the same initals?] | |||
= Multiple comparisons = | = Multiple comparisons = | ||
| Line 792: | Line 1,108: | ||
* [http://varianceexplained.org/statistics/interpreting-pvalue-histogram/ Plot a histogram of p-values], a post from varianceexplained.org. The anti-conservative histogram (tail on the RHS) is what we have typically seen in e.g. microarray gene expression data. | * [http://varianceexplained.org/statistics/interpreting-pvalue-histogram/ Plot a histogram of p-values], a post from varianceexplained.org. The anti-conservative histogram (tail on the RHS) is what we have typically seen in e.g. microarray gene expression data. | ||
* [http://statistic-on-air.blogspot.com/2015/01/adjustment-for-multiple-comparison.html Comparison of different ways of multiple-comparison] in R. | * [http://statistic-on-air.blogspot.com/2015/01/adjustment-for-multiple-comparison.html Comparison of different ways of multiple-comparison] in R. | ||
* [https://peerj.com/articles/10387/ Comparing multiple comparisons: practical guidance for choosing the best multiple comparisons test] Midway 2020 | |||
Take an example, Suppose 550 out of 10,000 genes are significant at .05 level | Take an example, Suppose 550 out of 10,000 genes are significant at .05 level | ||
| Line 799: | Line 1,116: | ||
According to [https://www.cancer.org/cancer/cancer-basics/lifetime-probability-of-developing-or-dying-from-cancer.html Lifetime Risk of Developing or Dying From Cancer], there is a 39.7% risk of developing a cancer for male during his lifetime (in other words, 1 out of every 2.52 men in US will develop some kind of cancer during his lifetime) and 37.6% for female. So the probability of getting at least one cancer patient in a 3-generation family is 1-.6**3 - .63**3 = 0.95. | According to [https://www.cancer.org/cancer/cancer-basics/lifetime-probability-of-developing-or-dying-from-cancer.html Lifetime Risk of Developing or Dying From Cancer], there is a 39.7% risk of developing a cancer for male during his lifetime (in other words, 1 out of every 2.52 men in US will develop some kind of cancer during his lifetime) and 37.6% for female. So the probability of getting at least one cancer patient in a 3-generation family is 1-.6**3 - .63**3 = 0.95. | ||
== Flexible method == | |||
[https://rdrr.io/bioc/GSEABenchmarkeR/man/runDE.html ?GSEABenchmarkeR::runDE]. Unadjusted (too few DE genes), FDR, and Bonferroni (too many DE genes) are applied depending on the proportion of DE genes. | |||
== Family-Wise Error Rate (FWER) == | == Family-Wise Error Rate (FWER) == | ||
[https://rviews.rstudio.com/2019/10/02/multiple-hypothesis-testing/ Multiple Hypothesis Testing in R] | * https://en.wikipedia.org/wiki/Family-wise_error_rate | ||
* [https://www.statology.org/family-wise-error-rate/ How to Estimate the Family-wise Error Rate] | |||
* [https://rviews.rstudio.com/2019/10/02/multiple-hypothesis-testing/ Multiple Hypothesis Testing in R] | |||
== Bonferroni == | == Bonferroni == | ||
| Line 812: | Line 1,134: | ||
* [https://youtu.be/K8LQSvtjcEo False Discovery Rates, FDR, clearly explained] by StatQuest | * [https://youtu.be/K8LQSvtjcEo False Discovery Rates, FDR, clearly explained] by StatQuest | ||
* A [http://xkcd.com/882/ comic] | * A [http://xkcd.com/882/ comic] | ||
* [http://www.nonlinear.com/support/progenesis/comet/faq/v2.0/pq-values.aspx A p-value of 0.05 implies that 5% of all tests will result in false positives. An FDR adjusted p-value (or q-value) of 0.05 implies that 5% of significant tests will result in false positives. The latter will result in fewer false positives]. | |||
* [https://stats.stackexchange.com/a/456087 How to interpret False Discovery Rate?] | |||
* P-value vs false discovery rate vs family wise error rate. See [http://jtleek.com/talks 10 statistics tip] or [http://www.biostat.jhsph.edu/~jleek/teaching/2011/genomics/mt140688.pdf#page=14 Statistics for Genomics (140.688)] from Jeff Leek. Suppose 550 out of 10,000 genes are significant at .05 level | * P-value vs false discovery rate vs family wise error rate. See [http://jtleek.com/talks 10 statistics tip] or [http://www.biostat.jhsph.edu/~jleek/teaching/2011/genomics/mt140688.pdf#page=14 Statistics for Genomics (140.688)] from Jeff Leek. Suppose 550 out of 10,000 genes are significant at .05 level | ||
** P-value < .05 implies expecting .05*10000 = 500 false positives | ** P-value < .05 implies expecting .05*10000 = 500 false positives (if we consider 50 hallmark genesets, 50*.05=2.5) | ||
** False discovery rate < .05 implies expecting .05*550 = 27.5 false positives | ** False discovery rate < .05 implies expecting .05*550 = 27.5 false positives | ||
** Family wise error rate (P (# of false positives ≥ 1)) < .05. See [https://riffyn.com/riffyn-blog/2017/10/29/family-wise-error-rate Understanding Family-Wise Error Rate] | ** Family wise error rate (P (# of false positives ≥ 1)) < .05. See [https://riffyn.com/riffyn-blog/2017/10/29/family-wise-error-rate Understanding Family-Wise Error Rate] | ||
| Line 822: | Line 1,146: | ||
* [https://academic.oup.com/bioinformatics/advance-article/doi/10.1093/bioinformatics/btz191/5380770 onlineFDR]: an R package to control the false discovery rate for growing data repositories | * [https://academic.oup.com/bioinformatics/advance-article/doi/10.1093/bioinformatics/btz191/5380770 onlineFDR]: an R package to control the false discovery rate for growing data repositories | ||
* [https://academic.oup.com/biostatistics/article/15/1/1/244509#2869827 An estimate of the science-wise false discovery rate and application to the top medical literature] Jager & Leek 2021 | * [https://academic.oup.com/biostatistics/article/15/1/1/244509#2869827 An estimate of the science-wise false discovery rate and application to the top medical literature] Jager & Leek 2021 | ||
* The adjusted p-value (also known as the False Discovery Rate or FDR) and the raw p-value can be close under certain conditions. [https://stats.stackexchange.com/a/51159 study on multiple outcomes- do I adjust or not adjust p-values?] | |||
** '''The number of tests is small''': When performing multiple hypothesis tests, the adjustment for multiple comparisons (like Bonferroni or Benjamini-Hochberg procedures) can have a smaller impact if the number of tests is small. This is because these adjustments are less stringent when fewer tests are conducted. | |||
** '''The p-values are very small''': If the raw p-values are very small to begin with, then even after adjustment, they may still remain small. This is especially true for methods that control the FDR, like the Benjamini-Hochberg procedure, which tend to be less conservative than methods controlling the Family-Wise Error Rate (FWER), like the Bonferroni correction. | |||
** '''The tests are not independent''': Some p-value adjustment methods assume that the tests are independent. If this assumption is violated, the adjusted p-values may not be accurate. | |||
* [https://predictivehacks.com/the-benjamini-hochberg-procedure-fdr-and-p-value-adjusted-explained/ The Benjamini-Hochberg Procedure (FDR) And P-Value Adjusted Explained] | |||
Suppose <math>p_1 \leq p_2 \leq ... \leq p_n</math>. Then | Suppose <math>p_1 \leq p_2 \leq ... \leq p_n</math>. Then | ||
| Line 827: | Line 1,156: | ||
\text{FDR}_i = \text{min}(1, n* p_i/i) | \text{FDR}_i = \text{min}(1, n* p_i/i) | ||
</math>. | </math>. | ||
* If the number of tests (<math>n</math>) is large and/or the original p value (<math>p_i</math>) is large, then FDR can hit the value 1. | |||
* For large n, | |||
** For early ranks (small 𝑖), the '''multiplier <math>n/i</math>''' is large. But if you’re at the top of the list with a very small raw p-value, the adjusted value can still stay small, because the raw p is tiny enough to survive the scaling. | |||
** '''For middle/late ranks (larger i)''', the factor <math>n/i</math> is smaller (closer to 1), '''so adjusted p-values are closer to the raw p'''. | |||
Below is the histograms of p-values and FDR (BH adjusted) from a real data (Pomeroy in BRB-ArrayTools). | * '''Monotonic adjustment''' | ||
** The simple formula above does not guarantee the monotonicity property from the FDR. So the calculation in R is more complicated. See [https://stackoverflow.com/questions/29992944/how-does-r-calculate-the-false-discovery-rate How Does R Calculate the False Discovery Rate]. | |||
[[:File:Hist bh.svg]] | ** Example: if pval=c(0.01,0.02,0.021,0.04,0.05), then p.adjust(pval, "BH") = c(.035, .035, .035, .050, .050) instead c(.05, .05, .035, .05, .05) if we only apply the formula n*p/i. So the adjusted p is applying the backward cumulative minimum to enforce monotonicity. | ||
*** n/i*pi = c(.05, .05, .035, .05, .05) | |||
And the next is a scatterplot w/ histograms on the margins from a null data. | *** Apply the '''backward cumulative minimum'''. i=5 -> .05. i=4 -> min(.05, .05)=.05, i=3 -> min(.035, .05)=.035, i=2 -> min(.05, .035)=.035. i=1 -> min(0.05, .035) = .035. | ||
** To ensure interpretability, the standard BH implementation applies a '''correction step'''. This makes the adjusted p-values non-decreasing with rank <math>i</math>. | |||
[[:File:Scatterhist.svg]] | :: <math> | ||
p_{(i)}^{BH} = \min_{j \geq i} (\frac{n}{j} * p_{(j)}) | |||
</math> | |||
* Below is the histograms of p-values and FDR (BH adjusted) from a real data (Pomeroy in BRB-ArrayTools). [[:File:Hist bh.svg]] | |||
* And the next is a scatterplot w/ histograms on the margins from a null data. The curve looks like f(x)=log(x). [[:File:Scatterhist.svg]] | |||
== q-value == | == q-value == | ||
| Line 860: | Line 1,193: | ||
* [https://en.wikipedia.org/wiki/Resampling_(statistics)#Permutation_tests Permutation tests] | * [https://en.wikipedia.org/wiki/Resampling_(statistics)#Permutation_tests Permutation tests] | ||
* https://stats.stackexchange.com/a/80879 | * https://stats.stackexchange.com/a/80879 | ||
* Multinomial coefficient. [https://www.rdocumentation.org/packages/iterpc/versions/0.4.2/topics/multichoose multichoose()] | |||
<syntaxhighlight lang='r'> | |||
library("iterpc") | |||
multichoose(c(3,1,1)) # [1] 20 | |||
multichoose(c(10,10)) |> log10() # [1] 5.266599 | |||
multichoose(c(100,100), bigz = T) |> log10() # [1] 58.95688 | |||
multichoose(c(100,100,100), bigz = T) |> log10() # [1] 140.5758 | |||
</syntaxhighlight> | |||
== Multivariate permutation test == | == Multivariate permutation test == | ||
| Line 976: | Line 1,318: | ||
== Test of overdispersion or underdispersion in Poisson models == | == Test of overdispersion or underdispersion in Poisson models == | ||
https://stats.stackexchange.com/questions/66586/is-there-a-test-to-determine-whether-glm-overdispersion-is-significant | https://stats.stackexchange.com/questions/66586/is-there-a-test-to-determine-whether-glm-overdispersion-is-significant | ||
== Poisson == | |||
* https://en.wikipedia.org/wiki/Poisson_distribution | |||
* [https://www.tandfonline.com/doi/abs/10.1080/00031305.2022.2046159 The “Poisson” Distribution: History, Reenactments, Adaptations] | |||
* [https://www.zeileis.org/news/poisson/ The Poisson distribution: From basic probability theory to regression models] | |||
* [https://www.dataquest.io/blog/tutorial-poisson-regression-in-r/ Tutorial: Poisson Regression in R] | |||
* We can use a '''quasipoisson''' model, which allows the variance to be proportional rather than equal to the mean. glm(, family="quasipoisson", ). | |||
** [https://sscc.wisc.edu/sscc/pubs/glm-r/ Generalized Linear Models in R] from sscc.wisc. | |||
** See the R code in the supplement of the paper [https://academic.oup.com/ije/article/46/1/348/2622842 Interrupted time series regression for the evaluation of public health interventions: a tutorial] 2016 | |||
== Negative Binomial == | == Negative Binomial == | ||
| Line 987: | Line 1,338: | ||
** [https://www.rdatagen.net/post/2021-01-05-coming-soon-new-feature-to-easily-generate-cumulative-odds-without-proportionality-assumption/ Coming soon: effortlessly generate ordinal data without assuming proportional odds] | ** [https://www.rdatagen.net/post/2021-01-05-coming-soon-new-feature-to-easily-generate-cumulative-odds-without-proportionality-assumption/ Coming soon: effortlessly generate ordinal data without assuming proportional odds] | ||
** [https://www.rdatagen.net/post/2021-03-02-randomization-tests/ Randomization tests] | ** [https://www.rdatagen.net/post/2021-03-02-randomization-tests/ Randomization tests] | ||
* [https://www.tandfonline.com/doi/full/10.1080/00031305.2024.2350445 Binomial Confidence Intervals for Rare Events: Importance of Defining Margin of Error Relative to Magnitude of Proportion]. Wald, Clopper-Pearson (exact), Wilson and Agresti-Coull. | |||
= Count data = | = Count data = | ||
| Line 1,046: | Line 1,398: | ||
</pre> | </pre> | ||
</li> | </li> | ||
<li>[https://www.r-bloggers.com/2025/05/downsampling-for-predictive-modeling/ Downsampling for predictive modeling] | |||
</ul> | </ul> | ||
== Odds ratio == | == Odds ratio == | ||
Calculate the odds ratio from the coefficient estimates; see [https://stats.stackexchange.com/questions/8661/logistic-regression-in-r-odds-ratio this post]. | <ul> | ||
<li> https://en.wikipedia.org/wiki/Odds_ratio. | |||
* Odds ratio was used in the case of '''2x2 contingency table'''. | |||
* Odds ratio can be applied to the '''logistic regression'''. | |||
* It seems a larger OR does not imply a smaller Fisher's exact p-value. See an example on Fig 4 [https://ascopubs.org/doi/figure/10.1200/PO.19.00345 here]. | |||
<li>Odds ratio = exp(coefficient). For example, if the coefficient for a predictor variable in your logistic regression model is 0.5, the odds ratio for that variable would be: exp(0.5) = 1.64. This means that, for every unit increase in the predictor variable, the '''odds''' of the binary outcome occurring increase by a factor of 1.64. A larger odds ratio indicates a stronger association between the predictor variable and the binary outcome, while a smaller odds ratio indicates a weaker association. | |||
<li>'''Why the odds ratio is exp(coefficient) in logistic regression?''' The odds ratio is the exponent of the coefficient in a logistic regression model because the logistic regression model is based on the '''logit function, which is the natural logarithm of the odds ratio'''. The logit function takes the following form: '''logit(p) = log(p/(1-p))''', where p is the probability of the binary outcome occurring. | |||
<li>Clinical example: Imagine that you are conducting a study to investigate the association between body mass index (''BMI'') and the risk of developing ''type 2 diabetes''. Fit a logistic regression using BMI as the covariate. Calculate the odds ratio for the BMI variable: exp(coefficient) = 1.64. This means that, for every unit increase in BMI, the odds of a patient developing type 2 diabetes increase by a factor of 1.64. | |||
<li>'''Probability vs. odds''': Probability and odds can differ from each other in many ways. For example, probability (of an event) typically appears as a percentage, while you can express odds as a ''fraction or ratio'' (the ratio of the number of ways the event can occur to the number of ways it cannot occur). Another difference is that probability uses a range that only exists between the numbers zero and one, while odds use a range that has no limits. | |||
<li> Calculate the odds ratio from the coefficient estimates; see [https://stats.stackexchange.com/questions/8661/logistic-regression-in-r-odds-ratio this post]. | |||
{{Pre}} | {{Pre}} | ||
require(MASS) | require(MASS) | ||
| Line 1,064: | Line 1,426: | ||
exp(cbind(coef(glmFit), confint(glmFit))) | exp(cbind(coef(glmFit), confint(glmFit))) | ||
</pre> | </pre> | ||
</ul> | |||
== AUC == | == AUC == | ||
| Line 1,079: | Line 1,442: | ||
= Medical applications = | = Medical applications = | ||
== RCT == | == RCT == | ||
[https://www.rdatagen.net/post/2021-11-23-design-effects-with-baseline-measurements/ The design effect of a cluster randomized trial with baseline measurements] | * [https://www.rdatagen.net/post/2021-11-23-design-effects-with-baseline-measurements/ The design effect of a cluster randomized trial with baseline measurements] | ||
* [https://www.r-bloggers.com/2024/09/explaining-a-causal-forest/ Explaining a Causal Forest] | |||
* [https://www.tandfonline.com/doi/full/10.1080/00031305.2025.2468399?af=R An Example to Illustrate Randomized Trial Estimands and Estimators] | |||
* [https://www.r-bloggers.com/2025/05/planning-for-a-3-arm-cluster-randomized-trial-with-a-nested-intervention-and-a-time-to-event-outcome/ Planning for a 3-arm cluster randomized trial with a nested intervention and a time-to-event outcome] | |||
== Subgroup analysis == | == Subgroup analysis == | ||
| Line 1,090: | Line 1,456: | ||
* [https://rpsychologist.com/treatment-response-subgroup Change over time is not "treatment response"] | * [https://rpsychologist.com/treatment-response-subgroup Change over time is not "treatment response"] | ||
* [https://www.tandfonline.com/doi/full/10.1080/01621459.2020.1740096?journalCode=uasa20 Inference on Selected Subgroups in Clinical Trials] Guo 2020 | * [https://www.tandfonline.com/doi/full/10.1080/01621459.2020.1740096?journalCode=uasa20 Inference on Selected Subgroups in Clinical Trials] Guo 2020 | ||
* [https://cran.r-project.org/web/packages/BioPred/index.html BioPred] - An R Package for Biomarkers Analysis in Precision Medicine. [https://academic.oup.com/bioinformatics/article/40/10/btae592/7815021 Bioinformatics] 2024 | |||
== Interaction analysis == | == Interaction analysis == | ||
| Line 1,146: | Line 1,513: | ||
* [http://statweb.stanford.edu/~tibs/research.html An Introduction to Statistical Learning with Applications in R]/ISLR], [https://github.com/tpn/pdfs/blob/master/An%20Introduction%20To%20Statistical%20Learning%20with%20Applications%20in%20R%20(ISLR%20Sixth%20Printing).pdf pdf] | * [http://statweb.stanford.edu/~tibs/research.html An Introduction to Statistical Learning with Applications in R]/ISLR], [https://github.com/tpn/pdfs/blob/master/An%20Introduction%20To%20Statistical%20Learning%20with%20Applications%20in%20R%20(ISLR%20Sixth%20Printing).pdf pdf] | ||
** https://www.statlearning.com/ 2nd edition. Aug 2021. [https://cran.r-project.org/web/packages/ISLR2/index.html ISLR2] package. | ** https://www.statlearning.com/ 2nd edition. Aug 2021. [https://cran.r-project.org/web/packages/ISLR2/index.html ISLR2] package. | ||
** https://r4ds.github.io/bookclub-islr/ | |||
** [https://www.dataschool.io/15-hours-of-expert-machine-learning-videos/amp/?s=09 In-depth introduction to machine learning in 15 hours of expert videos] | ** [https://www.dataschool.io/15-hours-of-expert-machine-learning-videos/amp/?s=09 In-depth introduction to machine learning in 15 hours of expert videos] | ||
** [https://emilhvitfeldt.github.io/ISLR-tidymodels-labs/index.html *Translations of the labs into using the tidymodels set of packages] | ** [https://emilhvitfeldt.github.io/ISLR-tidymodels-labs/index.html *Translations of the labs into using the tidymodels set of packages] | ||
* [https://comp-approach.com/ A Computational Approach to Statistical Learning] by Taylor Arnold, Michael Kane, and Bryan Lewis. [https://comp-approach.com/chapter08.pdf Chap 8 Neural Networks]. | |||
* [http://heather.cs.ucdavis.edu/draftregclass.pdf From Linear Models to Machine Learning] by Norman Matloff | * [http://heather.cs.ucdavis.edu/draftregclass.pdf From Linear Models to Machine Learning] by Norman Matloff | ||
* [http://www.kdnuggets.com/2017/04/10-free-must-read-books-machine-learning-data-science.html 10 Free Must-Read Books for Machine Learning and Data Science] | * [http://www.kdnuggets.com/2017/04/10-free-must-read-books-machine-learning-data-science.html 10 Free Must-Read Books for Machine Learning and Data Science] | ||
| Line 1,165: | Line 1,536: | ||
== LDA (Fisher's linear discriminant), QDA == | == LDA (Fisher's linear discriminant), QDA == | ||
* https://en.wikipedia.org/wiki/Linear_discriminant_analysis | * https://en.wikipedia.org/wiki/Linear_discriminant_analysis. | ||
** Assumptions: '''Multivariate normality, Homogeneity of variance/covariance''', Multicollinearity, Independence. | |||
** The common variance is calculated by the pooled covariance matrix just like the [[T-test#Two_sample_test_assuming_equal_variance|t-test case]]. | |||
** ''Logistic regression has none-the-less become the common choice, since the assumptions of discriminant analysis are rarely met.'' | |||
* [https://datascienceplus.com/how-to-perform-logistic-regression-lda-qda-in-r/ How to perform Logistic Regression, LDA, & QDA in R] | * [https://datascienceplus.com/how-to-perform-logistic-regression-lda-qda-in-r/ How to perform Logistic Regression, LDA, & QDA in R] | ||
* [http://r-posts.com/discriminant-analysis-statistics-all-the-way/ Discriminant Analysis: Statistics All The Way] | * [http://r-posts.com/discriminant-analysis-statistics-all-the-way/ Discriminant Analysis: Statistics All The Way] | ||
* [https://onlinelibrary.wiley.com/doi/10.1111/biom.13065 Multiclass linear discriminant analysis with ultrahigh‐dimensional features] Li 2019 | * [https://onlinelibrary.wiley.com/doi/10.1111/biom.13065 Multiclass linear discriminant analysis with ultrahigh‐dimensional features] Li 2019 | ||
* [https://sebastianraschka.com/Articles/2014_python_lda.html Linear Discriminant Analysis – Bit by Bit] | |||
== Bagging == | == Bagging == | ||
| Line 1,188: | Line 1,563: | ||
* http://www.is.uni-freiburg.de/ressourcen/business-analytics/10_ensemblelearning.pdf and [http://www.is.uni-freiburg.de/ressourcen/business-analytics/homework_ensemblelearning_questions.pdf exercise] | * http://www.is.uni-freiburg.de/ressourcen/business-analytics/10_ensemblelearning.pdf and [http://www.is.uni-freiburg.de/ressourcen/business-analytics/homework_ensemblelearning_questions.pdf exercise] | ||
* [https://freakonometrics.hypotheses.org/52782 Classification from scratch] | * [https://freakonometrics.hypotheses.org/52782 Classification from scratch] | ||
* [https://datasciencetut.com/boosting-in-machine-learning/ Boosting in Machine Learning:-A Brief Overview] | |||
=== AdaBoost === | === AdaBoost === | ||
| Line 1,272: | Line 1,648: | ||
* [http://www.santanupattanayak.com/2017/12/19/newtons-method-vs-gradient-descent-method-in-tacking-saddle-points-in-non-convex-optimization/ Newton's Method vs Gradient Descent Method in tacking saddle points in Non-Convex Optimization] | * [http://www.santanupattanayak.com/2017/12/19/newtons-method-vs-gradient-descent-method-in-tacking-saddle-points-in-non-convex-optimization/ Newton's Method vs Gradient Descent Method in tacking saddle points in Non-Convex Optimization] | ||
* [https://dinh-hung-tu.github.io/gradient-descent-vs-newton-method/ Gradient Descent vs Newton Method] | * [https://dinh-hung-tu.github.io/gradient-descent-vs-newton-method/ Gradient Descent vs Newton Method] | ||
== Double descent == | |||
[https://www.r-bloggers.com/2025/10/double-descent-explained/ Double Descent Explained] | |||
== Classification and Regression Trees (CART) == | == Classification and Regression Trees (CART) == | ||
| Line 1,290: | Line 1,669: | ||
* [http://cran.r-project.org/web/packages/rpart/vignettes/longintro.pdf rpart] | * [http://cran.r-project.org/web/packages/rpart/vignettes/longintro.pdf rpart] | ||
* http://exploringdatablog.blogspot.com/2013/04/classification-tree-models.html | * http://exploringdatablog.blogspot.com/2013/04/classification-tree-models.html | ||
* [https://cran.r-project.org/web/packages/parttree/index.html parttree]: Visualize Simple 2-D Decision Tree Partitions | |||
== Partially additive (generalized) linear model trees == | == Partially additive (generalized) linear model trees == | ||
| Line 1,318: | Line 1,698: | ||
* https://en.wikipedia.org/wiki/Mallows%27s_Cp | * https://en.wikipedia.org/wiki/Mallows%27s_Cp | ||
* [https://www.jobnmadu.com/r-blog/2023-02-04-r-rmarkdown/mallows/ Better and enhanced method of estimating Mallow's Cp] | |||
* Used in Yuan & Lin (2006) group lasso. The degrees of freedom is estimated by the bootstrap or perturbation methods. Their paper mentioned the performance is comparable with that of 5-fold CV but is computationally much faster. | * Used in Yuan & Lin (2006) group lasso. The degrees of freedom is estimated by the bootstrap or perturbation methods. Their paper mentioned the performance is comparable with that of 5-fold CV but is computationally much faster. | ||
| Line 1,338: | Line 1,719: | ||
== Support vector machine (SVM) == | == Support vector machine (SVM) == | ||
* [https://statcompute.wordpress.com/2016/03/19/improve-svm-tuning-through-parallelism/ Improve SVM tuning through parallelism] by using the '''foreach''' and '''doParallel''' packages. | * [https://statcompute.wordpress.com/2016/03/19/improve-svm-tuning-through-parallelism/ Improve SVM tuning through parallelism] by using the '''foreach''' and '''doParallel''' packages. | ||
* [https://www.spsanderson.com/steveondata/posts/2023-09-11/index.html Plotting SVM Decision Boundaries with e1071 in R] | |||
== Quadratic Discriminant Analysis (qda), KNN == | == Quadratic Discriminant Analysis (qda), KNN == | ||
| Line 1,463: | Line 1,845: | ||
== Postprediction inference/Inference based on predicted outcomes == | == Postprediction inference/Inference based on predicted outcomes == | ||
[https://www.pnas.org/content/117/48/30266 Methods for correcting inference based on outcomes predicted by machine learning] Wang 2020. [https://github.com/leekgroup/postpi postpi] package. | [https://www.pnas.org/content/117/48/30266 Methods for correcting inference based on outcomes predicted by machine learning] Wang 2020. [https://github.com/leekgroup/postpi postpi] package. | ||
== SHAP/SHapley Additive exPlanation: feature importance for each class == | |||
<ul> | |||
<li>https://en.wikipedia.org/wiki/Shapley_value | |||
<li>Python https://shap.readthedocs.io/en/latest/index.html | |||
<li>[https://towardsdatascience.com/introduction-to-shap-with-python-d27edc23c454 Introduction to SHAP with Python]. For a given prediction, SHAP values can tell us how much each factor in a model has contributed to the prediction. | |||
<li>[https://towardsdatascience.com/a-novel-approach-to-feature-importance-shapley-additive-explanations-d18af30fc21b A Novel Approach to Feature Importance — Shapley Additive Explanations] | |||
<li>[https://towardsdatascience.com/shap-shapley-additive-explanations-5a2a271ed9c3 SHAP: Shapley Additive Explanations] | |||
<li>R package [https://cran.r-project.org/web/packages/shapr/ shapr]: Prediction Explanation with Dependence-Aware Shapley Values | |||
* The output of Shapley value produced by explain() is an n_test x (1+p_test) matrix where "n" is the number of obs and "p" is the dimension of predictor. | |||
* The Shapley values can be plotted using a barplot for each test sample. | |||
* '''approach''' parameter can be empirical/gaussian/copula/ctree. See [https://rdrr.io/cran/shapr/man/ doc] | |||
* Note the package only supports a few prediction models to be used in the '''shapr''' function. | |||
<pre> | |||
$ debug(shapr:::get_supported_models) | |||
$ shapr:::get_supported_models() | |||
Browse[2]> print(DT) | |||
model_class get_model_specs predict_model | |||
1: default FALSE TRUE | |||
2: gam TRUE TRUE | |||
3: glm TRUE TRUE | |||
4: lm TRUE TRUE | |||
5: ranger TRUE TRUE | |||
6: xgb.Booster TRUE TRUE | |||
</pre> | |||
</li> | |||
<li>[https://blog.datascienceheroes.com/how-to-interpret-shap-values-in-r/ A gentle introduction to SHAP values in R] '''xgboost''' package | |||
<li>[https://stackoverflow.com/a/71886457 Create SHAP plots for tidymodels objects] | |||
<li>[https://cran.r-project.org/web/packages/shapper/index.html shapper]: Wrapper of Python Library 'shap' | |||
<li>[https://lorentzen.ch/index.php/2022/12/21/interpret-complex-linear-models-with-shap-within-seconds/ Interpret Complex Linear Models with SHAP within Seconds] | |||
<li>[https://www.r-bloggers.com/2024/06/shap-values-of-additive-models/ SHAP Values of Additive Models] | |||
<li>[https://www.r-bloggers.com/2025/09/key-improvements-in-shapviz-and-kernelshap/ Key improvements in shapviz and kernelshap] | |||
</ul> | |||
= Imbalanced/unbalanced Classification = | = Imbalanced/unbalanced Classification = | ||
| Line 1,503: | Line 1,918: | ||
* [https://jasonkerwin.com/nonparibus/2017/09/25/randomization-inference-vs-bootstrapping-p-values/ Randomization inference vs. bootstrapping for p-values] | * [https://jasonkerwin.com/nonparibus/2017/09/25/randomization-inference-vs-bootstrapping-p-values/ Randomization inference vs. bootstrapping for p-values] | ||
= | == Randomization test == | ||
[https://www.tandfonline.com/doi/full/10.1080/01621459.2023.2199814 What is a Randomization Test?] | |||
= | == Myths of randomisation == | ||
[https://www.growkudos.com/publications/10.1002%25252Fsim.5713/reader Myths of randomisation] | |||
== | == Unequal probabilities == | ||
[https://www.r-bloggers.com/2024/08/sampling-without-replacement-with-unequal-probabilities-by-ellis2013nz/ Sampling without replacement with unequal probabilities] | |||
= | = Model selection criteria = | ||
[ | * [http://r-video-tutorial.blogspot.com/2017/07/assessing-accuracy-of-our-models-r.html Assessing the Accuracy of our models (R Squared, Adjusted R Squared, RMSE, MAE, AIC)] | ||
* | * [https://forecasting.svetunkov.ru/en/2018/03/22/comparing-additive-and-multiplicative-regressions-using-aic-in-r/ Comparing additive and multiplicative regressions using AIC in R] | ||
* | * [https://www.tandfonline.com/doi/full/10.1080/00031305.2018.1459316?src=recsys Model Selection and Regression t-Statistics] Derryberry 2019 | ||
* | * Mean Absolute Deviance. Measure of the average absolute difference between the predicted values and the actual values. | ||
* | * Cf: [https://en.wikipedia.org/wiki/Average_absolute_deviation Mean absolute deviation], [https://en.wikipedia.org/wiki/Median_absolute_deviation Median absolute deviation]. Measure of the variability. | ||
== | == All models are wrong == | ||
[https://en.wikipedia.org/wiki/All_models_are_wrong All models are wrong] from George Box. | |||
== | == MSE == | ||
[ | * [https://stats.stackexchange.com/a/306337 Is MSE decreasing with increasing number of explanatory variables?] Yes | ||
== Akaike information criterion/AIC == | |||
* https://en.wikipedia.org/wiki/Akaike_information_criterion. | |||
:<math>\mathrm{AIC} \, = \, 2k - 2\ln(\hat L)</math>, where k be the number of estimated parameters in the model. | |||
* Smaller is better (error criteria) | |||
* Akaike proposed to approximate the expectation of the cross-validated log likelihood <math>E_{test}E_{train} [log L(x_{test}| \hat{\beta}_{train})]</math> by <math>log L(x_{train} | \hat{\beta}_{train})-k </math>. | |||
* Leave-one-out cross-validation is asymptotically equivalent to AIC, for ordinary linear regression models. | |||
* AIC can be used to compare two models even if they are not hierarchically nested. | |||
* [https://www.rdocumentation.org/packages/stats/versions/3.6.0/topics/AIC AIC()] from the stats package. | |||
* [https://broom.tidymodels.org/reference/glance.lm.html broom::glance()] was used. | |||
* Generally resampling based measures such as cross-validation should be preferred over theoretical measures such as Aikake's Information Criteria. [http://scott.fortmann-roe.com/docs/BiasVariance.html Understanding the Bias-Variance Tradeoff] & [http://scott.fortmann-roe.com/docs/MeasuringError.html Accurately Measuring Model Prediction Error]. | |||
== BIC == | |||
:<math>\mathrm{BIC} \, = \, \ln(n) \cdot 2k - 2\ln(\hat L)</math>, where k be the number of estimated parameters in the model. | |||
== Overfitting == | |||
* [https://stats.stackexchange.com/questions/81576/how-to-judge-if-a-supervised-machine-learning-model-is-overfitting-or-not How to judge if a supervised machine learning model is overfitting or not?] | |||
* [https://win-vector.com/2021/01/04/the-nature-of-overfitting/ The Nature of Overfitting], [https://win-vector.com/2021/01/07/smoothing-isnt-always-safe/ Smoothing isn’t Always Safe] | |||
[https:// | == AIC vs AUC == | ||
[https://stats.stackexchange.com/a/51278 What is the difference in what AIC and c-statistic (AUC) actually measure for model fit?] | |||
Roughly speaking: | |||
* AIC is telling you how good your model fits for a specific mis-classification cost. | |||
* AUC is telling you how good your model would work, on average, across all mis-classification costs. | |||
'''Frank Harrell''': AUC (C-index) has the advantage of measuring the concordance probability as you stated, aside from cost/utility considerations. To me the bottom line is the AUC should be used to describe discrimination of one model, not to compare 2 models. For comparison we need to use the most powerful measure: deviance and those things derived from deviance: generalized 𝑅<sup>2</sup> and AIC. | |||
</ | |||
== | == Variable selection and model estimation == | ||
[https://stats.stackexchange.com/a/138475 Proper variable selection: Use only training data or full data?] | |||
* training observations to perform all aspects of model-fitting—including variable selection | |||
* make use of the full data set in order to obtain more accurate coefficient estimates (This statement is arguable) | |||
= Cross-Validation = | |||
References: | |||
* [https://arxiv.org/abs/2104.00673 Cross-validation: what does it estimate and how well does it do it?], [https://www.tandfonline.com/doi/full/10.1080/01621459.2023.2197686 JASA] 2023 | |||
R packages: | |||
* [https://cran.r-project.org/web/packages/rsample/index.html rsample] (released July 2017). An [https://leekgroup.github.io/postpi/doc/vignettes.html example] from the postpi package. | |||
* [https://cran.r-project.org/web/packages/CrossValidate/index.html CrossValidate] (released July 2017) | |||
* [https://github.com/thierrymoudiki/crossval crossval] (github, new home at https://techtonique.r-universe.dev/), | |||
** [https://thierrymoudiki.github.io/blog/2020/05/08/r/misc/crossval-custom-errors Custom errors for cross-validation using crossval::crossval_ml] | |||
** [https://thierrymoudiki.github.io/blog/2021/07/23/r/crossvalidation-r-universe crossvalidation on R-universe, plus a classification example] | |||
== | == Bias–variance tradeoff == | ||
<ul> | |||
<li>[https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff Wikipedia] | |||
<li>[https://www.simplilearn.com/tutorials/machine-learning-tutorial/bias-and-variance Everything You Need To Know About Bias And Variance]. Y-axis = error, X-axis = model complexity. | |||
* | <li>[https://datacadamia.com/data_mining/bias_trade-off#model_complexity_is_betterworse Statistics - Bias-variance trade-off (between overfitting and underfitting)] | ||
<li>[https://statisticallearning.org/bias-variance-tradeoff.html *Chapter 4 The Bias–Variance Tradeoff] from Basics of Statistical Learning by David Dalpiaz. R code is included. Regression case. | |||
<li>Ridge regression | |||
* <math>Obj = (y-X \beta)^T (y - X \beta) + \lambda ||\beta||_2^2 </math> | |||
* [https://lbelzile.github.io/lineaRmodels/bias-and-variance-tradeoff.html Plot of MSE, bias**2, variance of ridge estimator in terms of lambda] by Léo Belzile. Note that there is a typo in the bias term. It should be <math>E(\gamma)-\gamma = [(Z^TZ+\lambda I_p)^{-1}Z^TZ -I_p] \lambda </math>. | |||
* [https://www.statlect.com/fundamentals-of-statistics/ridge-regression Explicit form of the bias and variance] of ridge estimator. The estimator is linear. <math>\hat{\beta} = (X^T X + \lambda I_p)^{-1} (X^T y) </math> | |||
</ul> | |||
== | == Data splitting == | ||
[[Prediction#CV|Prediction -> CV]] | |||
== | == PRESS statistic (LOOCV) in regression, Predicted R² == | ||
[ | * The [https://en.wikipedia.org/wiki/PRESS_statistic PRESS statistic] (predicted residual error sum of squares) <math>\sum_i (y_i - \hat{y}_{i,-i})^2</math> provides another way to find the optimal model in regression. | ||
See the [https://lbelzile.github.io/lineaRmodels/cross-validation-1.html formula for the ridge regression] case. | |||
* [https://www.r-bloggers.com/2025/04/explained-vs-predictive-power-r%c2%b2-adjusted-r%c2%b2-and-beyond/ Explained vs. Predictive Power: R², Adjusted R², and Beyond] | |||
== | == LOOCV vs 10-fold CV in classification == | ||
[https:// | * Background: [https://en.wikipedia.org/wiki/Variance#Sum_of_correlated_variables Variance of mean] for correlated data. If the variables have equal variance ''σ''<sup>2</sup> and the average correlation of distinct variables is ''ρ'', then the variance of their mean is | ||
== | :<math>\operatorname{Var}\left(\overline{X}\right) = \frac{\sigma^2}{n} + \frac{n - 1}{n}\rho\sigma^2.</math> | ||
[https:// | :This implies that the variance of the mean increases with the average of the correlations. | ||
* ([https://hastie.su.domains/ISLR2/ISLRv2_website.pdf#page=214 5.1.4 of ISLR 2nd]) | |||
** k-fold CV is that it often gives more accurate estimates of the test error rate than does LOOCV. This has to do with a bias-variance trade-off. | |||
** '''When we perform LOOCV, we are in effect averaging the outputs of n fitted models, each of which is trained on an almost identical set of observations; therefore, these outputs are highly (positively) correlated with each other.''' Since the mean of many highly correlated quantities has higher variance than does the mean of many quantities that are not as highly correlated, the test error estimate resulting from LOOCV tends to have higher variance than does the test error estimate resulting from k-fold CV... Typically, given these considerations, one performs k-fold cross-validation using k = 5 or k = 10, as these values have been shown empirically to yield test error rate estimates that suffer neither from excessively high bias nor from very high variance. | |||
* [https://stats.stackexchange.com/a/264721 10-fold Cross-validation vs leave-one-out cross-validation] | |||
** Leave-one-out cross-validation is approximately unbiased. But it tends to have a high '''variance'''. | |||
** The '''variance''' in fitting the model tends to be higher if it is fitted to a small dataset. | |||
** In LOOCV, because there is a lot of overlap between training sets, and thus the test error estimates are highly correlated, which means that the mean value of the test error estimate will have higher '''variance'''. | |||
** Unless the dataset were very small, I would use 10-fold cross-validation if it fitted in my computational budget, or better still, bootstrap estimation and bagging. | |||
* [https://web.stanford.edu/~hastie/ISLR2/ISLRv2_website.pdf#page=213 Chapter 5 Resampling Methods] of ISLR 2nd. | |||
* [https://r4ds.github.io/bookclub-islr/bias-variance-tradeoff-and-k-fold-cross-validation.html Bias-Variance Tradeoff and k-fold Cross-Validation] | |||
* [https://stats.stackexchange.com/a/90903 Why is leave-one-out cross-validation (LOOCV) variance about the mean estimate for error high?] | |||
* [https://stats.stackexchange.com/a/178421 High variance of leave-one-out cross-validation] | |||
* [https://brb.nci.nih.gov/techreport/TechReport_Molinaro.pdf Prediction Error Estimation: A Comparison of Resampling Methods] Molinaro 2005 | |||
* Survival data [https://brb.nci.nih.gov/techreport/Subramanina-Simon-StatMed.pdf An evaluation of resampling methods for assessment of survival risk prediction in high-dimensional settings] Subramanian 2010 | |||
* [https://brb.nci.nih.gov/techreport/Briefings.pdf#page=10 Using cross-validation to evaluate predictive accuracy of survival risk classifiers based on high-dimensional data] Subramanian 2011. | |||
** classification error: (Molinaro 2005) For small sample sizes of fewer than 50 cases, they recommended use of leave-one-out cross-validation to minimize mean squared error of the estimate of prediction error. | |||
** survival data using time-dependent ROC: (Subramanian 2010) They recommended use of 5- or 10-fold cross-validation for a wide range of conditions | |||
== | == Monte carlo cross-validation == | ||
This method creates multiple random splits of the dataset into training and validation data. See [https://en.wikipedia.org/wiki/Cross-validation_(statistics)#Repeated_random_sub-sampling_validation Wikipedia]. | |||
* It is not creating replicates of CV samples. | |||
* As the number of random splits approaches infinity, the result of repeated random sub-sampling validation tends towards that of leave-p-out cross-validation. | |||
* | |||
* | |||
= | == Difference between CV & bootstrapping == | ||
[https://stats.stackexchange.com/a/18355 Differences between cross validation and bootstrapping to estimate the prediction error] | |||
* CV tends to be less biased but K-fold CV has fairly large variance. | |||
* Bootstrapping tends to drastically reduce the variance but gives more biased results (they tend to be pessimistic). | |||
* The 632 and 632+ rules methods have been adapted to deal with the bootstrap bias | |||
* Repeated CV does K-fold several times and averages the results similar to regular K-fold | |||
= | == .632 and .632+ bootstrap == | ||
* 0.632 bootstrap: Efron's paper [https://www.jstor.org/stable/pdf/2288636.pdf Estimating the Error Rate of a Prediction Rule: Improvement on Cross-Validation] in 1983. | |||
* | * 0.632+ bootstrap: The CV estimate of prediction error is nearly unbiased but can be highly variable. See [https://www.tandfonline.com/doi/pdf/10.1080/01621459.1997.10474007 Improvements on Cross-Validation: The .632+ Bootstrap Method] by Efron and Tibshirani, JASA 1997. | ||
* [ | * Chap 17.7 from "An Introduction to the Bootstrap" by Efron and Tibshirani. Chapman & Hall. | ||
* | * Chap 7.4 (resubstitution error <math>\overline{err} </math>) and chap 7.11 (<math>Err_{boot(1)}</math>leave-one-out bootstrap estimate of prediction error) from "The Elements of Statistical Learning" by Hastie, Tibshirani and Friedman. Springer. | ||
* ( | * [http://stats.stackexchange.com/questions/96739/what-is-the-632-rule-in-bootstrapping What is the .632 bootstrap]? | ||
* ( | : <math> | ||
* [ | Err_{.632} = 0.368 \overline{err} + 0.632 Err_{boot(1)} | ||
* [https:// | </math> | ||
* [https://www. | * [https://link.springer.com/referenceworkentry/10.1007/978-1-4419-9863-7_1328 Bootstrap, 0.632 Bootstrap, 0.632+ Bootstrap] from Encyclopedia of Systems Biology by Springer. | ||
* [https:// | * bootpred() from bootstrap function. | ||
* [https:// | * The .632 bootstrap estimate can be extended to statistics other than prediction error. See the paper [https://www.tandfonline.com/doi/full/10.1080/10543406.2016.1226329 Issues in developing multivariable molecular signatures for guiding clinical care decisions] by Sachs. [https://github.com/sachsmc/signature-tutorial Source code]. Let <math>\phi</math> be a performance metric, <math>S_b</math> a sample of size n from a bootstrap, <math>S_{-b}</math> subset of <math>S</math> that is disjoint from <math>S_b</math>; test set. | ||
: <math> | |||
<ul> | \hat{E}^*[\phi_{\mathcal{F}}(S)] = .368 \hat{E}[\phi_{f}(S)] + 0.632 \hat{E}[\phi_{f_b}(S_{-b})] | ||
<li>[ | </math> | ||
: where <math>\hat{E}[\phi_{f}(S)]</math> is the naive estimate of <math>\phi_f</math> using the entire dataset. | |||
* For survival data | |||
** [https://cran.r-project.org/web/packages/ROC632/ ROC632] package, [https://repositorium.sdum.uminho.pt/bitstream/1822/52744/1/paper4_final_version_CatarinaSantos_ACB.pdf Overview], and the paper [https://www.degruyter.com/view/j/sagmb.2012.11.issue-6/1544-6115.1815/1544-6115.1815.xml?format=INT Time Dependent ROC Curves for the Estimation of True Prognostic Capacity of Microarray Data] by Founcher 2012. | |||
** [https://onlinelibrary.wiley.com/doi/full/10.1111/j.1541-0420.2007.00832.x Efron-Type Measures of Prediction Error for Survival Analysis] Gerds 2007. | |||
** [https://academic.oup.com/bioinformatics/article/23/14/1768/188061 Assessment of survival prediction models based on microarray data] Schumacher 2007. Brier score. | |||
** [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4194196/ Evaluating Random Forests for Survival Analysis using Prediction Error Curves] Mogensen, 2012. [https://cran.r-project.org/web/packages/pec/ pec] package | |||
** [https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/1471-2288-12-102 Assessment of performance of survival prediction models for cancer prognosis] Chen 2012. Concordance, ROC... But bootstrap was not used. | |||
** [https://www.sciencedirect.com/science/article/pii/S1672022916300390#b0150 Comparison of Cox Model Methods in A Low-dimensional Setting with Few Events] 2016. Concordance, calibration slopes RMSE are considered. | |||
== Create partitions for cross-validation == | |||
Stratified sampling: caret::createFolds() or [https://rsample.tidymodels.org/reference/vfold_cv.html rsample::vfold_cv] (used in tidymodels specifically) | |||
<ul> | |||
<li>[http://r-exercises.com/2016/11/13/sampling-exercise-1/ set.seed(), sample.split(),createDataPartition(), and createFolds()] functions from the [https://github.com/cran/caret/blob/master/R/createDataPartition.R caret] package. [https://topepo.github.io/caret/data-splitting.html Simple Splitting with Important Groups]. [https://rdrr.io/rforge/caret/src/R/createFolds.R ?createFolds], [https://gist.github.com/mrecos/47a201af97d8d218beb6 Stratified K-folds Cross-Validation with Caret] | |||
<pre> | <pre> | ||
# Stratified sampling | |||
library(caret) | |||
set.seed(1) | |||
x <- sample(rep(c("A", "B"), c(100, 200))) # 1:2 ratio | |||
folds <- createFolds(x, k = 5, list = TRUE, returnTrain = FALSE) | |||
# Confirm that each fold has approximately the same proportion of samples | |||
# for each unique value in the target variable | |||
for(i in 1:5) print(prop.table(table(x[folds[[i]]]))) # 1:2 ratio | |||
length(unique(union(union(union(union(folds[[1]], folds[[2]]), folds[[3]]), folds[[4]]), folds[[5]]))) | |||
# [1] 300 | |||
</pre> | </pre> | ||
<pre> | <pre> | ||
library( | library(rsample) | ||
# Stratified 5-fold CV on iris data | |||
cv_rs <- vfold_cv(iris, v = 5, strata = Species) | |||
# First fold | |||
train1 <- analysis(cv_rs$splits[[1]]) | |||
test1 <- assessment(cv_rs$splits[[1]]) | |||
table(train1$Species) | |||
table(test1$Species) | |||
</pre> | </pre> | ||
</ul> | </ul> | ||
Random sampling: sample() | |||
<ul> | <ul> | ||
<li> | <li>[https://github.com/cran/glmnet/blob/master/R/cv.glmnet.R#L245 cv.glmnet()] | ||
[https:// | |||
<pre> | <pre> | ||
sample(rep(seq(nfolds), length = N)) # a vector | |||
set.seed(1); sample(rep(seq(3), length = 20)) | |||
# [1] 1 1 1 2 1 1 2 2 2 3 3 2 3 1 3 3 3 1 2 2 | |||
</pre> | </pre> | ||
= | <li>Another way is to use '''replace=TRUE''' in sample() (not quite uniform compared to the last method, strange) | ||
<pre> | |||
sample(1:nfolds, N, replace=TRUE) # a vector | |||
set.seed(1); sample(1:3, 20, replace=TRUE) | |||
# [1] 1 3 1 2 1 3 3 2 2 3 3 1 1 1 2 2 2 2 3 1 | |||
table(.Last.value) | |||
# .Last.value | |||
# 1 2 3 | |||
# 7 7 6 | |||
</pre> | |||
<li>[https://drsimonj.svbtle.com/k-fold-cross-validation-with-modelr-and-broom k-fold cross validation with modelr and broom] | |||
<li>[https://cran.r-project.org/web/packages/h2o/index.html h2o] package to [https://bmccancer.biomedcentral.com/track/pdf/10.1186/s12885-018-4546-8#page=4 split the merged training dataset into three parts] | |||
<pre> | |||
n <- 42; nfold <- 5 # unequal partition | |||
folds <- split(sample(1:n), rep(1:nfold, length = n)) # a list | |||
sapply(folds, length) | |||
</pre> | |||
<li>Another simple example. Split the data into 70% training data and 30% testing data | |||
<pre> | |||
mysplit <- sample(c(rep(0, 0.7 * nrow(df)), rep(1, nrow(df) - 0.7 * nrow(df)))) | |||
train <- df[mysplit == 0, ] | |||
test <- df[mysplit == 1, ] | |||
</pre> | |||
</ul> | |||
== | == Create training/testing data == | ||
<ul> | |||
<li>[https://rdrr.io/rforge/caret/man/createDataPartition.html ?createDataPartition]. | |||
<li>[https://stackoverflow.com/a/46591859 caret createDataPartition returns more samples than expected]. It is more complicated than it looks. | |||
<pre> | |||
set.seed(1) | |||
createDataPartition(rnorm(10), p=.3) | |||
# $Resample1 | |||
# [1] 1 2 4 5 | |||
= | set.seed(1) | ||
:< | createDataPartition(rnorm(10), p=.5) | ||
# $Resample1 | |||
# [1] 1 2 4 5 6 9 | |||
</pre> | |||
<li>[https://www.r-bloggers.com/2024/07/stratified-sampling-in-r-a-practical-guide-with-base-r-and-dplyr/ Stratified Sampling in R: A Practical Guide with Base R and dplyr] | |||
<li>[https://en.wikipedia.org/wiki/Stratified_sampling Stratified sampling]: [https://www.statology.org/stratified-sampling-r/ Stratified Sampling in R (With Examples)], [https://rsample.tidymodels.org/reference/initial_split.html initial_split()] from tidymodels. '''With a strata argument, the random sampling is conducted within the stratification variable'''. So it guaranteed each strata (stratify variable level) has observations in training and testing sets. | |||
<pre> | |||
> library(rsample) # or library(tidymodels) | |||
> table(mtcars$cyl) | |||
4 6 8 | |||
11 7 14 | |||
> set.seed(22) | |||
> sp <- initial_split(mtcars, prop=.8, strata = cyl) | |||
# 80% training and 20% testing sets | |||
> table(training(sp)$cyl) | |||
4 6 8 | |||
8 5 11 | |||
> table(testing(sp)$cyl) | |||
4 6 8 | |||
3 2 3 | |||
> 8/11; 5/7; 11/14 # split by initial_split() | |||
[1] 0.7272727 | |||
[1] 0.7142857 | |||
[1] 0.7857143 | |||
> 9/11; 6/7; 12/14 # if we try to increase 1 observation | |||
[1] 0.8181818 | |||
[1] 0.8571429 | |||
[1] 0.8571429 | |||
> (8+5+11)/nrow(mtcars) | |||
[1] 0.75 | |||
> (9+6+12)/nrow(mtcars) | |||
[1] 0.84375 # looks better | |||
> set.seed(22) | |||
> sp2 <- initial_split(mtcars, prop=.8) | |||
table(training(sp2)$cyl) | |||
4 6 8 | |||
8 7 10 | |||
> table(testing(sp2)$cyl) | |||
4 8 | |||
3 4 | |||
# not what we want since cyl "6" has no observations | |||
</pre> | |||
</ul> | |||
== | == Nested resampling == | ||
[https://stats.stackexchange.com/ | * [http://appliedpredictivemodeling.com/blog/2017/9/2/njdc83d01pzysvvlgik02t5qnaljnd Nested Resampling with rsample] | ||
* [https://github.com/compstat-lmu/lecture_i2ml/tree/master/slides-pdf Introduction to Machine Learning (I2ML)] | |||
* https://stats.stackexchange.com/questions/292179/whats-the-meaning-of-nested-resampling | |||
Nested resampling is need when we want to '''tuning a model''' by using a grid search. The default settings of a model are likely not optimal for each data set out. So an inner CV has to be performed with the aim to find the best parameter set of a learner for each fold. | |||
See a diagram at https://i.stack.imgur.com/vh1sZ.png | |||
In BRB-ArrayTools -> class prediction with multiple methods, the ''alpha'' (significant level of threshold used for gene selection, 2nd option in individual genes) can be viewed as a tuning parameter for the development of a classifier. | |||
* | == Pre-validation/pre-validated predictor == | ||
* | * [https://www.degruyter.com/view/j/sagmb.2002.1.1/sagmb.2002.1.1.1000/sagmb.2002.1.1.1000.xml Pre-validation and inference in microarrays] Tibshirani and Efron, Statistical Applications in Genetics and Molecular Biology, 2002. | ||
* See glmnet vignette | |||
* http://www.stat.columbia.edu/~tzheng/teaching/genetics/papers/tib_efron.pdf#page=5. In each CV, we compute the estimate of the response. This estimate of the response will serve as a new predictor ('''pre-validated 'predictor' ''') in the final fitting model. | |||
* P1101 of Sachs 2016. With pre-validation, instead of computing the statistic <math>\phi</math> for each of the held-out subsets (<math>S_{-b}</math> for the bootstrap or <math>S_{k}</math> for cross-validation), the fitted signature <math>\hat{f}(X_i)</math> is estimated for <math>X_i \in S_{-b}</math> where <math>\hat{f}</math> is estimated using <math>S_{b}</math>. This process is repeated to obtain a set of '''pre-validated 'signature' ''' estimates <math>\hat{f}</math>. Then an association measure <math>\phi</math> can be calculated using the pre-validated signature estimates and the true outcomes <math>Y_i, i = 1, \ldots, n</math>. | |||
* Another description from the paper [https://www.genetics.org/content/205/1/77 The Spike-and-Slab Lasso Generalized Linear Models for Prediction and Associated Genes Detection]. The prevalidation method is a variant of cross-validation. We then use <math>(y_i, \hat{\eta}_i) </math> to compute the measures described above. The cross-validated linear predictor for each patient is derived independently of the observed response of the patient, and hence the “prevalidated” dataset Embedded Image can essentially be treated as a “new dataset.” Therefore, this procedure provides valid assessment of the predictive performance of the model. To get stable results, we run 10× 10-fold cross-validation for real data analysis. | |||
* In CV, left-out samples = hold-out cases = test set | |||
= | == Custom cross validation == | ||
* [ | * [https://github.com/WinVector/vtreat vtreat package] | ||
* | * https://github.com/WinVector/vtreat/blob/master/Examples/CustomizedCrossPlan/CustomizedCrossPlan.md | ||
== | == Cross validation vs regularization == | ||
[http://www.win-vector.com/blog/2019/11/when-cross-validation-is-more-powerful-than-regularization/ When Cross-Validation is More Powerful than Regularization] | |||
== Cross-validation with confidence (CVC) == | |||
[https://amstat.tandfonline.com/doi/abs/10.1080/01621459.2019.1672556 JASA 2019] by Jing Lei, [https://arxiv.org/pdf/1703.07904.pdf pdf], [http://www.stat.cmu.edu/~jinglei/pub.shtml code] | |||
== | == Correlation data == | ||
[https://arxiv.org/pdf/1904.02438.pdf Cross-Validation for Correlated Data] Rabinowicz, JASA 2020 | |||
== Bias in Error Estimation == | |||
* [https://academic.oup.com/jnci/article/95/1/14/2520188#55882619 Pitfalls in the Use of DNA Microarray Data for Diagnostic and Prognostic Classification] Simon 2003. [https://github.com/arraytools/pitfalls My R code]. | |||
** Conclusion: '''Feature selection''' must be done within each cross-validation. Otherwise the selected feature already saw the labels of the training data, and made use of them. | |||
** Simulation: 2000 sets of 20 samples, of which 10 belonged to class 1 and the remaining 10 to class 2. Each sample was a vector of 6000 features (synthetic gene expressions). | |||
* [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1397873/ Bias in Error Estimation when Using Cross-Validation for Model Selection] Varma & Simon 2006 | |||
** Conclusion: '''Parameter tuning''' must be done within each cross-validation; '''nested CV''' is advocated. | |||
** Figures 1 (Shrunken centroids, shrinkage parameter Δ) & 2 (SVM, kernel parameters) are biased. Figure 3 (Shrunken centroids) & 4 (SVM) are unbiased. | |||
** For k-NN, the parameter is k. | |||
** Simulation: | |||
*** Null data: 1000 sets of 40 samples, of which 20 belonged to class 1 and the remaining 20 to class 2. Each sample was a vector of 6000 features (synthetic gene expressions). | |||
*** Non-null data: we simulated differential expression by fixing 10 genes (out of 6000) to have a population mean differential expression of 1 between the two classes. | |||
* Over-fitting and [https://www.jmlr.org/papers/volume11/cawley10a/cawley10a.pdf selection bias]; see [https://en.wikipedia.org/wiki/Cross-validation_(statistics) Cross-validation_(statistics)], [https://en.wikipedia.org/wiki/Selection_bias Selection bias] on Wikipedia. [https://twitter.com/sketchplanator/status/1409175698166763528 Comic]. | |||
* [https://arxiv.org/abs/1901.08974 On the cross-validation bias due to unsupervised pre-processing] Moscovich, 2019. [https://rss.onlinelibrary.wiley.com/doi/full/10.1111/rssb.12537?campaign=wolearlyview JRSSB] 2022 | |||
* [https://diagnprognres.biomedcentral.com/articles/10.1186/s41512-022-00126-w?s=09 Risk of bias of prognostic models developed using machine learning: a systematic review in oncology] Dhiman 2022 | |||
* [https://github.com/matloff/fastStat#lesson-over--predictive-modeling----avoiding-overfitting Avoiding Overfitting] from fastStat: All of REAL Statistics | |||
== Bias due to unsupervised preprocessing == | |||
[https://rss.onlinelibrary.wiley.com/doi/full/10.1111/rssb.12537 On the cross-validation bias due to unsupervised preprocessing] 2022. Below I follow the practice from [https://hpc.nih.gov/apps/python.html#envs Biowulf] to install Mamba. In this example, the 'project1' subfolder (2.0 GB) is located in '~/conda/envs' directory. | |||
{{Pre}} | |||
$ which python3 | |||
/usr/bin/python3 | |||
= | $ wget https://github.com/conda-forge/miniforge/releases/latest/download/Mambaforge-Linux-x86_64.sh | ||
$ bash Mambaforge-Linux-x86_64.sh -p /home/brb/conda -b | |||
$ source ~/conda/etc/profile.d/conda.sh && source ~/conda/etc/profile.d/mamba.sh | |||
$ mkdir -p ~/bin | |||
$ cat <<'__EOF__' > ~/bin/myconda | |||
__conda_setup="$('/home/$USER/conda/bin/conda' 'shell.bash' 'hook' 2> /dev/null)" | |||
if [ $? -eq 0 ]; then | |||
eval "$__conda_setup" | |||
else | |||
if [ -f "/home/$USER/conda/etc/profile.d/conda.sh" ]; then | |||
. "/home/$USER/conda/etc/profile.d/conda.sh" | |||
else | |||
export PATH="/home/$USER/conda/bin:$PATH" | |||
fi | |||
fi | |||
unset __conda_setup | |||
if [ -f "/home/$USER/conda/etc/profile.d/mamba.sh" ]; then | |||
. "/home/$USER/conda/etc/profile.d/mamba.sh" | |||
fi | |||
__EOF__ | |||
$ source ~/bin/myconda | |||
== | $ export MAMBA_NO_BANNER=1 | ||
$ mamba create -n project1 python=3.7 numpy scipy scikit-learn mkl-service mkl_random pandas matplotlib | |||
$ mamba activate project1 | |||
$ which python # /home/brb/conda/envs/project1/bin/python | |||
$ git clone https://github.com/mosco/unsupervised-preprocessing.git | |||
$ cd unsupervised-preprocessing/ | |||
$ python # Ctrl+d to quit | |||
$ mamba deactivate | |||
</pre> | |||
== Pitfalls of applying machine learning in genomics == | |||
[https://www.nature.com/articles/s41576-021-00434-9 Navigating the pitfalls of applying machine learning in genomics] 2022 | |||
= Bootstrap = | |||
See [[Bootstrap]] | |||
[ | = Clustering = | ||
See [[Heatmap#Clustering|Clustering]]. | |||
= Cross-sectional analysis = | |||
* https://en.wikipedia.org/wiki/Cross-sectional_study. The opposite of cross-sectional analysis is longitudinal analysis. | |||
* Cross-sectional analysis refers to a type of research method in which data is collected '''at a single point in time''' from a group of individuals, organizations, or other units of analysis. This approach contrasts with longitudinal studies, which follow the same group of individuals or units over an extended period of time. | |||
** In a cross-sectional analysis, researchers typically collect data from a sample of individuals or units that are representative of the population of interest. This data can then be used to examine patterns, relationships, or differences among the units at a specific point in time. | |||
** Cross-sectional analysis is commonly used in fields such as sociology, psychology, public health, and economics to study topics such as demographics, health behaviors, income inequality, and social attitudes. While cross-sectional analysis can provide valuable insights into the characteristics of a population at a given point in time, it cannot establish causality or determine changes over time. | |||
= Mixed Effect Model = | |||
See [[Longitudinal#Mixed_Effect_Model|Longitudinal analysis]]. | |||
= Entropy = | |||
* | * [http://theautomatic.net/2020/02/18/how-is-information-gain-calculated/ HOW IS INFORMATION GAIN CALCULATED?] | ||
* | * [https://youtu.be/YtebGVx-Fxw Entropy (for data science) Clearly Explained!!!] by StatQuest | ||
** | ** Entropy and [https://youtu.be/YtebGVx-Fxw?t=186 Surprise] and [https://youtu.be/YtebGVx-Fxw?t=951 surprise is in an inverse relationship to probability] | ||
** | ** [https://youtu.be/YtebGVx-Fxw?t=716 Entropy is an expectation of surprise] | ||
** | ** [https://youtu.be/YtebGVx-Fxw?t=921 Entropy can be used to quantify the similarity] | ||
** [https://youtu.be/YtebGVx-Fxw?t=931 Entropy is the highest when we have the same number of both types of chickens] | |||
: <math> | |||
\begin{align} | |||
Entropy &= \sum \log(1/p(x)) p(x) = \sum Surprise P(Surprise) | |||
\end{align} | |||
</math> | |||
== Definition == | |||
Entropy is defined by -log2(p) where p is a probability. '''Higher entropy represents higher unpredictable of an event'''. | |||
Some examples: | |||
* | * Fair 2-side die: Entropy = -.5*log2(.5) - .5*log2(.5) = 1. | ||
* | * Fair 6-side die: Entropy = -6*1/6*log2(1/6) = 2.58 | ||
* Weighted 6-side die: Consider pi=.1 for i=1,..,5 and p6=.5. Entropy = -5*.1*log2(.1) - .5*log2(.5) = 2.16 (less unpredictable than a fair 6-side die). | |||
= | == Use == | ||
When entropy was applied to the variable selection, we want to select a class variable which gives a largest entropy difference between without any class variable (compute entropy using response only) and with that class variable (entropy is computed by adding entropy in each class level) because this variable is most discriminative and it gives most '''information gain'''. For example, | |||
* | * entropy (without any class)=.94, | ||
* | * entropy(var 1) = .69, | ||
* | * entropy(var 2)=.91, | ||
* | * entropy(var 3)=.725. | ||
We will choose variable 1 since it gives the largest gain (.94 - .69) compared to the other variables (.94 -.91, .94 -.725). | |||
Why is picking the attribute with the most information gain beneficial? It ''reduces'' entropy, which increases predictability. A decrease in entropy signifies an decrease in unpredictability, which also means an increase in predictability. | |||
Consider a split of a continuous variable. Where should we cut the continuous variable to create a binary partition with the highest gain? Suppose cut point c1 creates an entropy .9 and another cut point c2 creates an entropy .1. We should choose c2. | |||
== | == Related == | ||
In addition to information gain, gini (dʒiːni) index is another metric used in decision tree. See [http://en.wikipedia.org/wiki/Decision_tree_learning wikipedia page] about decision tree learning. | |||
== | = Ensembles = | ||
[ | * Combining classifiers. Pro: better classification performance. Con: time consuming. | ||
* Comic http://flowingdata.com/2017/09/05/xkcd-ensemble-model/ | |||
* [http://www.win-vector.com/blog/2019/07/common-ensemble-models-can-be-biased/ Common Ensemble Models can be Biased] | |||
* [https://github.com/marjoleinf/pre?s=09 pre: an R package for deriving prediction rule ensembles]. It works on binary, multinomial, (multivariate) continuous, count and survival responses. | |||
== | == Bagging == | ||
Draw N bootstrap samples and summary the results (averaging for regression problem, majority vote for classification problem). Decrease variance without changing bias. Not help much with underfit or high bias models. | |||
== | === Random forest === | ||
* [https:// | * '''Variance importance''': if you scramble the values of a variable, and the accuracy of your tree does not change much, then the variable is not very important. | ||
* Why is it useful to compute variance importance? So the model's predictions are easier to interpret (not improve the prediction performance). | |||
* Random forest has advantages of easier to run in parallel and suitable for small n large p problems. | |||
* [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-018-2264-5 Random forest versus logistic regression: a large-scale benchmark experiment] by Raphael Couronné, BMC Bioinformatics 2018 | |||
* [https://github.com/suiji/arborist Arborist]: Parallelized, Extensible Random Forests | |||
* [https://academic.oup.com/bioinformatics/article-abstract/35/15/2701/5250706?redirectedFrom=fulltext On what to permute in test-based approaches for variable importance measures in Random Forests] | |||
* [https://datasandbox.netlify.app/posts/2022-10-03-tree%20based%20methods/ Tree Based Methods: Exploring the Forest] A study of the different tree based methods in machine learning . | |||
* It seems RF is good in classification problem. [https://thierrymoudiki.github.io/blog/2023/08/27/r/misc/crossvalidation-boxplots Comparing cross-validation results using crossval_ml and boxplots] | |||
* [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-024-05877-5 Random forests for the analysis of matched case–control studies] 2024 | |||
= | == Boosting == | ||
Instead of selecting data points randomly with the boostrap, it favors the misclassified points. | |||
Algorithm: | |||
* Initialize the weights | |||
* Repeat | |||
** resample with respect to weights | |||
** retrain the model | |||
** recompute weights | |||
Since boosting requires computation in iterative and bagging can be run in parallel, bagging has an advantage over boosting when the data is very large. | |||
== | == Time series == | ||
[https:// | * [https://petolau.github.io/Ensemble-of-trees-for-forecasting-time-series/ Ensemble learning for time series forecasting in R] | ||
* [https://blog.bguarisma.com/time-series-forecasting-lab-part-5-ensembles Time Series Forecasting Lab (Part 5) - Ensembles], [https://blog.bguarisma.com/time-series-forecasting-lab-part-6-stacked-ensembles Time Series Forecasting Lab (Part 6) - Stacked Ensembles] | |||
== | = p-values = | ||
[https:// | == p-values == | ||
* Prob(Data | H0) | |||
* https://en.wikipedia.org/wiki/P-value | |||
* [https://amstat.tandfonline.com/toc/utas20/73/sup1 Statistical Inference in the 21st Century: A World Beyond p < 0.05] The American Statistician, 2019 | |||
* [https://matloff.wordpress.com/2016/03/07/after-150-years-the-asa-says-no-to-p-values/ THE ASA SAYS NO TO P-VALUES] The problem is that with large samples, significance tests pounce on tiny, unimportant departures from the null hypothesis. We have the opposite problem with small samples: The power of the test is low, and we will announce that there is “no significant effect” when in fact we may have too little data to know whether the effect is important. | |||
* [http://www.r-statistics.com/2016/03/its-not-the-p-values-fault-reflections-on-the-recent-asa-statement/ It’s not the p-values’ fault] | |||
* [https://stablemarkets.wordpress.com/2016/05/21/exploring-p-values-with-simulations-in-r/ Exploring P-values with Simulations in R] from Stable Markets. | |||
* p-value and [https://en.wikipedia.org/wiki/Effect_size effect size]. http://journals.sagepub.com/doi/full/10.1177/1745691614553988 | |||
* [https://datascienceplus.com/ditch-p-values-use-bootstrap-confidence-intervals-instead/ Ditch p-values. Use Bootstrap confidence intervals instead] | |||
== Misuse of p-values == | |||
* https://en.wikipedia.org/wiki/Misuse_of_p-values. The p-value does not indicate the size or importance of the observed effect. | |||
* Question: If we are fitting a multivariate regression and variable 1 ends with p-value .01 and variable 2 has p-value .001. How do we describe variable 2 is more significant than variable 1? | |||
** Answer: you can say that variable 2 has a smaller p-value than variable 1. A p-value is a measure of the strength of evidence '''against the null hypothesis'''. It is the probability of observing a test statistic as extreme or more extreme than the one calculated from your data, assuming the null hypothesis is true. The smaller the p-value, the stronger the evidence '''against the null hypothesis''' and in favor of the alternative hypothesis. In your example, variable 2 has a smaller p-value than variable 1, which means that there is stronger evidence '''against the null hypothesis''' for variable 2 than for variable 1. <u>However, it is important to note that a smaller p-value does not necessarily mean that one variable has a stronger effect or is more important than the other.</u> Instead of comparing p-values directly, it would be more appropriate to look at '''effect sizes''' and '''confidence intervals''' to determine the relative importance of each variable. | |||
** '''Effect Size''': While a p-value tells you whether an effect exists, it does not convey the size of the effect. A p-value of 0.001 may be due to a larger effect size than one producing a p-value of 0.01, but ''this isn’t always the case''. '''Effect size measures (like Cohen’s d for two means, Pearson’s r for two continuous variables, or Odds Ratio in logistic regression or contingency tables)''' are necessary to interpret the practical significance. | |||
** '''Practical Significance''': Even if both p-values are statistically significant, the practical or clinical significance of the findings should be considered. A very small effect size, even with a p-value of 0.001, may not be practically important. | |||
* Question: do p-values show the relative importance of different predictors? | |||
* | ** P-values can indicate the statistical significance of a predictor in a model, but they do not directly measure the relative importance of different predictors. | ||
* | ** A p-value is a measure of the probability that the observed relationship between a predictor and the response variable occurred by chance under the null hypothesis. A smaller p-value suggests that it is less likely that the observed relationship occurred by chance, which often leads to the conclusion that the predictor is statistically significant. | ||
** However, p-values do not tell us about the size or magnitude of an effect, nor do they directly compare the effects of different predictors. ''Two predictors might both be statistically significant, but one might have a much larger '''effect''' on the response variable than the other'' (There are several statistical measures that can be used to assess the relative importance of predictors in a model: Standardized Coefficients, Partial Correlation Coefficients, Variable Importance in Projection (VIP), Variable Importance Measures in Tree-Based Models, LASSO (Least Absolute Shrinkage and Selection Operator) and Relative Weights Analysis). | |||
* | ** Moreover, p-values are sensitive to sample size. With a large enough sample size, even tiny, unimportant differences can become statistically significant. | ||
* | ** Therefore, while p-values are a useful tool in model analysis, they should not be used alone to determine the relative importance of predictors. Other statistical measures and domain knowledge should also be considered. | ||
* [https://freedium.cfd/https://medium.com/towards-data-science/why-statistical-significance-is-pointless-a7644be30266 Why "Statistical Significance" Is Pointless]. '''permutation p-value''', '''bootstrap confidence interval'''. | |||
[https:// | |||
== | == Distribution of p values in medical abstracts == | ||
[https:// | * http://www.ncbi.nlm.nih.gov/pubmed/26608725 | ||
* [https://github.com/jtleek/tidypvals An R package with several million published p-values in tidy data sets] by Jeff Leek. | |||
== | == nominal p-value and Empirical p-values == | ||
* Nominal p-values are based on asymptotic null distributions | |||
* Empirical p-values are computed from simulations/permutations | |||
* [https://stats.stackexchange.com/questions/536116/what-is-the-concepts-of-nominal-and-actual-significance-level What is the concepts of nominal and '''actual''' significance level?] | |||
** The nominal significance level is the significance level a test is designed to achieve. This is very often 5% or 1%. Now in many situations the nominal significance level can't be achieved precisely. This can happen because the distribution is discrete and doesn't allow for a precise given rejection probability, and/or because the theory behind the test is asymptotic, i.e., the nominal level is only achieved for 𝑛→∞. | |||
----- | |||
* | |||
* | |||
== | == (nominal) alpha level == | ||
Conventional methodology for statistical testing is, in advance of undertaking the test, to set a NOMINAL ALPHA CRITERION LEVEL (often 0.05). The outcome is classified as showing STATISTICAL SIGNIFICANCE if the actual ALPHA (probability of the outcome under the null hypothesis) is no greater than this NOMINAL ALPHA CRITERION LEVEL. | |||
* http://www.translationdirectory.com/glossaries/glossary033.htm | |||
* http:// | * http://courses.washington.edu/p209s07/lecturenotes/Week%205_Monday%20overheads.pdf | ||
== Normality assumption == | |||
[https://www.biorxiv.org/content/early/2018/12/20/498931 Violating the normality assumption may be the lesser of two evils] | |||
[ | |||
== Second-Generation p-Values == | |||
[https://amstat.tandfonline.com/doi/full/10.1080/00031305.2018.1537893 An Introduction to Second-Generation p-Values] Blume et al, 2020 | |||
[ | |||
== Small p-value due to very large sample size == | |||
* [https://stats.stackexchange.com/a/44466 How to correct for small p-value due to very large sample size] | |||
* [https://www.galitshmueli.com/system/files/Print%20Version.pdf Too big to fail: large samples and the p-value problem], Lin 2013. Cited by [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-018-2263-6#Sec17 ComBat] paper. | |||
* [https://stats.stackexchange.com/a/44466 How to correct for small p-value due to very large sample size] | |||
* [https://math.stackexchange.com/a/2939553 Does 𝑝-value change with sample size?] | |||
* [https://sebastiansauer.github.io/pvalue_sample_size/ The effect of sample on p-values. A simulation] | |||
* [https://data.library.virginia.edu/power-and-sample-size-analysis-using-simulation/ Power and Sample Size Analysis using Simulation] | |||
* [https://stats.stackexchange.com/questions/73045/simulating-p-values-as-a-function-of-sample-size Simulating p-values as a function of sample size] | |||
* [https://researchutopia.wordpress.com/2013/11/10/understanding-p-values-via-simulations/ Understanding p-values via simulations] | |||
* [https://www.r-bloggers.com/2018/04/p-values-sample-size-and-data-mining/ P-Values, Sample Size and Data Mining] | |||
== Bayesian == | |||
* Bayesian believers, who adhere to Bayesian statistics, often have a different perspective on hypothesis testing compared to '''frequentist statisticians'''. '''In Bayesian statistics, the focus is on estimating the probability of a hypothesis being true given the data, rather than on the probability of the data given a specific hypothesis (as in p-values).''' | |||
* Bayesian believers generally prefer using Bayesian methods, such as computing credible intervals or Bayes factors, which provide more directly interpretable results in terms of the probability of hypotheses. These methods can be seen as more informative than p-values, as they give a range of plausible values for the parameter of interest or directly compare the relative plausibility of different hypotheses. | |||
== [ | = T-statistic = | ||
See [[T-test#T-statistic|T-statistic]]. | |||
= ANOVA = | |||
See [[T-test#ANOVA|ANOVA]]. | |||
= [https://en.wikipedia.org/wiki/Goodness_of_fit Goodness of fit] = | |||
== [https://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test Chi-square tests] == | |||
* [http://freakonometrics.hypotheses.org/20531 An application of chi-square tests] | |||
== Fitting distribution == | |||
* [https://magesblog.com/post/2011-12-01-fitting-distributions-with-r/ Fitting distributions with R] | |||
* [https://www.r-bloggers.com/2024/10/automated-random-variable-distribution-inference-using-kullback-leibler-divergence-and-simulating-best-fitting-distribution/ Automated random variable distribution inference using Kullback-Leibler divergence and simulating best-fitting distribution] | |||
** [https://www.rdocumentation.org/packages/MASS/versions/7.3-61/topics/fitdistr MASS::fitdistr()] | |||
** Kullback-Leibler divergence for checking distribution adequacy | |||
== Normality distribution check == | |||
[https://finnstats.com/index.php/2021/11/09/anderson-darling-test-in-r/ Anderson-Darling Test in R (Quick Normality Check)] | |||
== Kolmogorov-Smirnov test == | |||
* [https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test Kolmogorov-Smirnov test] | |||
* An example of [https://gist.github.com/arraytools/d383f72a243a2e322004904ae6903610 manual calculations and ks.test()] | |||
** ks_1sample.R: calculate the KS test statistic for the one-sample case | |||
** ks_2sample.R: calculate the KS test statistic for two-sample distributions | |||
** ks_3sample.R: calculate the permutation p-value and compare it with the p-value from ks.test() | |||
* [https://online.stat.psu.edu/stat415/book/export/html/838 Lesson 22: Kolmogorov-Smirnov Goodness-of-Fit Test] from stat.psu. Easy to understand the calculation. | |||
* [https://www.rdocumentation.org/packages/dgof/versions/1.2/topics/ks.test ks.test()] in R | |||
* [https://www.statology.org/kolmogorov-smirnov-test-r/ Kolmogorov-Smirnov Test in R (With Examples)] | |||
* [https://rpubs.com/mharris/KSplot kolmogorov-smirnov plot] | |||
* [https://stackoverflow.com/a/27282758 Visualizing the Kolmogorov-Smirnov statistic in ggplot2] | |||
* [https://www.tandfonline.com/doi/full/10.1080/00031305.2024.2356095 On Misuses of the Kolmogorov–Smirnov Test for One-Sample Goodness-of-Fit] 2024 | |||
= Contingency Tables = | |||
[https://finnstats.com/index.php/2021/05/09/contingency-coefficient-association/ How to Measure Contingency-Coefficient (Association Strength)]. '''gplots::balloonplot()''' and '''corrplot::corrplot()''' . | |||
== What statistical test should I do == | |||
[https://statsandr.com/blog/what-statistical-test-should-i-do/ What statistical test should I do?] | |||
== Graphically show association == | |||
# '''Bar Graphs''': Bar graphs can be used to compare the frequency of different categories in two variables. Each bar represents a category, and the height of the bar represents its frequency. You can create side-by-side bar graphs or stacked bar graphs to compare frequencies across categories. See [https://statisticsbyjim.com/basics/contingency-table/ Contingency Table: Definition, Examples & Interpreting] (row totals) and [https://online.stat.psu.edu/stat100/lesson/6/6.1 Two Different Categorical Variables] (column totals). | |||
# '''Mosaic Plots''': A mosaic plot gives a visual representation of the relationship between two categorical variables. It's a rectangular grid that represents the total population, and it's divided into smaller rectangles that represent the categories of each variable. The size of each rectangle is proportional to the frequency of each category. See [https://yardsale8.github.io/stat110_book/chp3/mosaic.html Visualizing Association With Mosaic Plots]. | |||
# '''Categorical Scatterplots''': In seaborn, a Python data visualization library, there are categorical scatterplots that adjust the positions of points on the categorical axis with a small amount of random "jitter" or using an algorithm that prevents them from overlapping. See [https://seaborn.pydata.org/tutorial/categorical.html Visualizing categorical data]. | |||
# '''Contingency Tables''': While not a graphical method, contingency tables are often used in conjunction with graphical methods. A contingency table displays how many individuals fall in each combination of categories for two variables. | |||
Q: How to guess whether two variables are associated by looking at the counts in a 2x2 contingency table:<br> | |||
odds ratio | * '''Observe the distribution of counts''': If the counts are evenly distributed across the cells of the table, it suggests that there may not be a strong association between the two variables. However, if the counts are unevenly distributed, it suggests that there may be an association. | ||
* '''Compare the diagonal cells''': If the counts in the diagonal cells (top left to bottom right or top right to bottom left) are high compared to the off-diagonal cells, it suggests a '''positive association''' between the two variables. Conversely, if the counts in the off-diagonal cells are high, it suggests a '''negative association'''. See [[Statistics#Odds_ratio_and_Risk_ratio |odds ratio]] >1 (pos association) or <1 (neg association). | |||
* Calculate and compare the '''row and column totals''': If the row and column totals are similar, it suggests that there may not be a strong association between the two variables. However, if the row and column totals are very different, it suggests that there may be an association. | |||
[https:// | |||
Q: When creating a barplot of percentages from a contingency table, whether you calculate percentages by dividing counts by row totals or column totals? A: It depends on the question you’re trying to answer. See [https://statisticsbyjim.com/basics/contingency-table/ Contingency Table: Definition, Examples & Interpreting]. | |||
* '''Row Totals''': If you’re interested in understanding the distribution of a '''variable''' within each '''row category''', you would calculate percentages by dividing counts by row totals. This is often used when the '''row variable''' is the '''independent variable''' and you want to see how the column variable ('''dependent variable''') is distributed within each level of the row variable. | |||
* Column Totals: If you’re interested in understanding the distribution of a variable within each column category, you would calculate percentages by dividing counts by column totals. This is often used when the column variable is the independent variable and you want to see how the row variable (dependent variable) is distributed within each level of the column variable. | |||
[https://wiki.taichimd.us/view/Ggplot2#Barplot_with_colors_for_a_2nd_variable Barplot with colors for a 2nd variable]. | |||
== | == Measure the association in a contingency table == | ||
<ul> | |||
<li>'''Phi coefficient''': The Phi coefficient is a measure of association that is used for 2x2 contingency tables. It ranges from -1 to 1, with 0 indicating no association and values close to -1 or 1 indicating a strong association. The formula for Phi coefficient is: | |||
Phi = (ad - bc) / sqrt((a+b)(c+d)(a+c)(b+d)), where a, b, c, and d are the frequency counts in the four cells of the contingency table. | |||
<li>'''Cramer's V''': Cramer's V is a measure of association that is used for contingency tables of any size. It ranges from 0 to 1, with 0 indicating no association and values close to 1 indicating a strong association. The formula for Cramer's V is: | |||
V = sqrt(Chi-Square / (n*(min(r,c)-1))), where Chi-Square is the Chi-Square statistic, n is the total sample size, and r and c are the number of rows and columns in the contingency table. | |||
<li>'''Odds ratio''': The odds ratio is a measure of association that is commonly used in medical research and epidemiology. It compares the odds of an event occurring in one group compared to another group. The odds ratio can be calculated as: | |||
OR = (a/b) / (c/d), where a, b, c, and d are the frequency counts in the four cells of the contingency table. An odds ratio of 1 indicates no association, while values greater than 1 indicate a positive association and values less than 1 indicate a negative association. | |||
</ul> | |||
The | == Odds ratio and Risk ratio == | ||
<ul> | |||
<li>[https://en.wikipedia.org/wiki/Odds_ratio Odds ratio] and [https://en.wikipedia.org/wiki/Relative_risk Risk ratio/relative risk]. | |||
* In practice the odds ratio is commonly used for '''case-control studies''', as the relative risk cannot be estimated. | |||
* Relative risk is used in the statistical analysis of the data of ecological, cohort, medical and '''intervention studies''', to estimate the strength of the association between exposures (treatments or risk factors) and outcomes. | |||
<li>[https://www.r-bloggers.com/2022/02/odds-ratio-interpretation-quick-guide/ Odds Ratio Interpretation Quick Guide] </li> | |||
<li>The odds ratio is often used to evaluate the strength of the '''association''' between two binary variables and to compare the '''risk of an event''' occurring between two groups. | |||
* An odds ratio greater than 1 indicates that the event is more likely to occur in the first group, while an odds ratio less than 1 indicates that the event is more likely to occur in the second group. | |||
* In general, a larger odds ratio indicates a stronger association between the two variables, while a smaller odds ratio indicates a weaker association. | |||
<li>The ratio of the '''odds of an event''' occurring in one '''group''' to the odds of it occurring in another group | |||
<pre> | <pre> | ||
Treatment | Control | |||
------------------------------------------------- | |||
Event occurs | A | B | |||
------------------------------------------------- | |||
Event does not occur | C | D | |||
------------------------------------------------- | |||
Odds | A/C | B/D | |||
------------------------------------------------- | |||
Risk | A/(A+C) | B/(B+D) | |||
</pre> | |||
* '''Odds''' Ratio = (A / C) / (B / D) = (AD) / (BC) | |||
* '''Risk''' Ratio = (A / (A+C)) / (C / (B+D)) | |||
</li> | |||
<li>Real example. In a study published in the Journal of the American Medical Association, researchers investigated the '''association between''' the use of nonsteroidal anti-inflammatory drugs (''NSAIDs'') and the ''risk of developing gastrointestinal bleeding''. Suppose odds ratio = 2.5 and risk ratio is 1.5. The interpretation of the results in this study is as follows: | |||
* The odds ratio of 2.5 indicates that the odds of gastrointestinal bleeding are 2.5 times higher in the group of patients taking NSAIDs compared to the group of patients not taking NSAIDs. | |||
* The risk ratio of 1.5 indicates that the risk of gastrointestinal bleeding is 1.5 times higher in the group of patients taking NSAIDs compared to the group of patients not taking NSAIDs. | |||
* In this example, both the odds ratio and the risk ratio indicate a significant association between NSAID use and the risk of gastrointestinal bleeding. However, the risk ratio is lower than the odds ratio, indicating that the overall prevalence of gastrointestinal bleeding in the study population is relatively low. | |||
<li>What is the main difference in the interpretation of odds ratio and risk ratio? | |||
* Odds are a measure of the probability of an event occurring, expressed as the ratio of the number of ways the event can occur to the number of ways it cannot occur. For example, if the probability of an event occurring is 0.5 (or 50%), the odds of the event occurring would be 1:1 (or 1 to 1). | |||
* Risk is a measure of the probability of an event occurring, expressed as the ratio of the number of events that occur to the total number of events. For example, if 10 out of 100 people experience an event, the risk of the event occurring would be 10%. | |||
* The main difference between the two measures is that the odds ratio is more sensitive to changes in the '''frequency of the event''', while the risk ratio is more sensitive to changes in the '''overall prevalence of the event'''. | |||
* This means that the odds ratio is more useful for comparing the odds of an event occurring between two groups when the event is relatively '''rare''', while the risk ratio is more useful for comparing the risk of an event occurring between two groups when the event is more '''common'''. | |||
</ul> | |||
== Hypergeometric, One-tailed Fisher exact test == | |||
* [https://bioconductor.org/packages/release/bioc/vignettes/GSEABenchmarkeR/inst/doc/GSEABenchmarkeR.html ORA is inapplicable if there are few genes satisfying the significance threshold, or if almost all genes are DE]. See also the '''flexible''' adjustment method for the handling of multiple testing correction. | |||
* https://www.bioconductor.org/help/course-materials/2009/SeattleApr09/gsea/ (Are interesting features over-represented? or are selected genes more often in the ''GO category'' than expected by chance?) | |||
* https://en.wikipedia.org/wiki/Hypergeometric_distribution. '' In a test for over-representation of successes in the sample, the hypergeometric p-value is calculated as the probability of randomly drawing '''k''' or more successes from the population in '''n''' total draws. In a test for under-representation, the p-value is the probability of randomly drawing '''k''' or fewer successes.'' | |||
* http://stats.stackexchange.com/questions/62235/one-tailed-fishers-exact-test-and-the-hypergeometric-distribution | |||
* Two sided hypergeometric test | |||
** http://stats.stackexchange.com/questions/155189/how-to-make-a-two-tailed-hypergeometric-test | |||
** http://stats.stackexchange.com/questions/140107/p-value-in-a-two-tail-test-with-asymmetric-null-distribution | |||
** http://stats.stackexchange.com/questions/19195/explaining-two-tailed-tests | |||
* https://www.biostars.org/p/90662/ When computing the p-value (tail probability), consider to use 1 - Prob(observed -1) instead of 1 - Prob(observed) for discrete distribution. | |||
* https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Hypergeometric.html p(x) = choose(m, x) choose(n, k-x) / choose(m+n, k). | |||
<pre> | |||
drawn | not drawn | | |||
------------------------------------- | |||
white | x | | m | |||
------------------------------------- | |||
black | k-x | | n | |||
------------------------------------- | |||
| k | | m+n | |||
</pre> | |||
For example, k=100, m=100, m+n=1000, | |||
{{Pre}} | |||
> 1 - phyper(10, 100, 10^3-100, 100, log.p=F) | |||
[1] 0.4160339 | |||
> a <- dhyper(0:10, 100, 10^3-100, 100) | |||
> cumsum(rev(a)) | |||
[1] 1.566158e-140 1.409558e-135 3.136408e-131 3.067025e-127 1.668004e-123 5.739613e-120 1.355765e-116 | |||
[8] 2.325536e-113 3.018276e-110 3.058586e-107 2.480543e-104 1.642534e-101 9.027724e-99 4.175767e-96 | |||
[15] 1.644702e-93 5.572070e-91 1.638079e-88 4.210963e-86 9.530281e-84 1.910424e-81 3.410345e-79 | |||
[22] 5.447786e-77 7.821658e-75 1.013356e-72 1.189000e-70 1.267638e-68 1.231736e-66 1.093852e-64 | |||
[29] 8.900857e-63 6.652193e-61 4.576232e-59 2.903632e-57 1.702481e-55 9.240350e-54 4.650130e-52 | |||
[36] 2.173043e-50 9.442985e-49 3.820823e-47 1.441257e-45 5.074077e-44 1.669028e-42 5.134399e-41 | |||
[43] 1.478542e-39 3.989016e-38 1.009089e-36 2.395206e-35 5.338260e-34 1.117816e-32 2.200410e-31 | |||
[50] 4.074043e-30 7.098105e-29 1.164233e-27 1.798390e-26 2.617103e-25 3.589044e-24 4.639451e-23 | |||
[57] 5.654244e-22 6.497925e-21 7.042397e-20 7.198582e-19 6.940175e-18 6.310859e-17 5.412268e-16 | |||
[64] 4.377256e-15 3.338067e-14 2.399811e-13 1.626091e-12 1.038184e-11 6.243346e-11 3.535115e-10 | |||
[71] 1.883810e-09 9.442711e-09 4.449741e-08 1.970041e-07 8.188671e-07 3.193112e-06 1.167109e-05 | |||
[78] 3.994913e-05 1.279299e-04 3.828641e-04 1.069633e-03 2.786293e-03 6.759071e-03 1.525017e-02 | |||
[85] 3.196401e-02 6.216690e-02 1.120899e-01 1.872547e-01 2.898395e-01 4.160339e-01 5.550192e-01 | |||
[92] 6.909666e-01 8.079129e-01 8.953150e-01 9.511926e-01 9.811343e-01 9.942110e-01 9.986807e-01 | |||
[99] 9.998018e-01 9.999853e-01 1.000000e+00 | |||
# Density plot | |||
plot(0:100, dhyper(0:100, 100, 10^3-100, 100), type='h') | |||
</pre> | |||
[[:File:Dhyper.svg]] | |||
Moreover, | |||
<pre> | |||
1 - phyper(q=10, m, n, k) | |||
= 1 - sum_{x=0}^{x=10} phyper(x, m, n, k) | |||
= 1 - sum(a[1:11]) # R's index starts from 1. | |||
</pre> | |||
data: | Another example is the data from [https://david.ncifcrf.gov/helps/functional_annotation.html#fisher the functional annotation tool] in DAVID. | ||
<pre> | |||
| gene list | not gene list | | |||
------------------------------------------------------- | |||
pathway | 3 (q) | | 40 (m) | |||
------------------------------------------------------- | |||
not in pathway | 297 | | 29960 (n) | |||
------------------------------------------------------- | |||
| 300 (k) | | 30000 | |||
</pre> | </pre> | ||
The one-tailed p-value from the hypergeometric test is calculated as 1 - phyper(3-1, 40, 29960, 300) = 0.0074. | |||
== | == [https://en.wikipedia.org/wiki/Fisher%27s_exact_test Fisher's exact test] == | ||
Following the above example from the DAVID website, the following R command calculates the Fisher exact test for independence in 2x2 contingency tables. | |||
{{Pre}} | |||
> fisher.test(matrix(c(3, 40, 297, 29960), nr=2)) # alternative = "two.sided" by default | |||
Fisher's Exact Test for Count Data | |||
data: matrix(c(3, 40, 297, 29960), nr = 2) | |||
p-value = 0.008853 | |||
alternative hypothesis: true odds ratio is not equal to 1 | |||
= | 95 percent confidence interval: | ||
1.488738 23.966741 | |||
sample estimates: | |||
odds ratio | |||
7.564602 | |||
> fisher.test(matrix(c(3, 40, 297, 29960), nr=2), alternative="greater") | |||
Fisher's Exact Test for Count Data | |||
= | data: matrix(c(3, 40, 297, 29960), nr = 2) | ||
p-value = 0.008853 | |||
alternative hypothesis: true odds ratio is greater than 1 | |||
95 percent confidence interval: | |||
1.973 Inf | |||
sample estimates: | |||
odds ratio | |||
7.564602 | |||
= | > fisher.test(matrix(c(3, 40, 297, 29960), nr=2), alternative="less") | ||
* Diagonal structure: <math>\sigma_{ij} = 0</math> if <math>i \neq j</math>. | Fisher's Exact Test for Count Data | ||
* Compound symmetry: <math>\sigma_{ij} = \rho</math> if <math>i \neq j</math>. | |||
* First-order autoregressive AR(1) structure: <math>\sigma_{ij} = \rho^{|i - j|}</math>. <syntaxhighlight lang='rsplus'> | data: matrix(c(3, 40, 297, 29960), nr = 2) | ||
p-value = 0.9991 | |||
alternative hypothesis: true odds ratio is less than 1 | |||
95 percent confidence interval: | |||
0.00000 20.90259 | |||
sample estimates: | |||
odds ratio | |||
7.564602 | |||
</pre> | |||
[https://www.statsandr.com/blog/fisher-s-exact-test-in-r-independence-test-for-a-small-sample/ Fisher's exact test in R: independence test for a small sample] | |||
From the documentation of [https://stat.ethz.ch/R-manual/R-devel/library/stats/html/fisher.test.html fisher.test] | |||
<pre> | |||
Usage: | |||
fisher.test(x, y = NULL, workspace = 200000, hybrid = FALSE, | |||
control = list(), or = 1, alternative = "two.sided", | |||
conf.int = TRUE, conf.level = 0.95, | |||
simulate.p.value = FALSE, B = 2000) | |||
</pre> | |||
* For 2 by 2 cases, p-values are obtained directly using the (central or non-central) hypergeometric distribution. | |||
* For 2 by 2 tables, the null of conditional independence is equivalent to the hypothesis that the odds ratio equals one. | |||
* The alternative for a one-sided test is based on the odds ratio, so ‘alternative = "greater"’ is a test of the odds ratio being bigger than ‘or’. | |||
* Two-sided tests are based on the probabilities of the tables, and take as ‘more extreme’ all tables with probabilities less than or equal to that of the observed table, the p-value being the sum of such probabilities. | |||
== Boschloo's test == | |||
https://en.wikipedia.org/wiki/Boschloo%27s_test | |||
== IID assumption == | |||
[https://www.r-bloggers.com/2024/06/ignoring-the-iid-assumption-isnt-a-great-idea/ Ignoring the IID assumption isn’t a great idea] | |||
== Chi-square independence test == | |||
* https://en.wikipedia.org/wiki/Chi-squared_test. | |||
** Chi-Square = Σ[(O - E)^2 / E] | |||
** We can see expected_{ij} = n_{i.}*n_{.j}/n_{..} | |||
** The Chi-Square test statistic follows a Chi-Square distribution with degrees of freedom equal to (r-1) x (c-1) | |||
** The Chi-Square test is generally a '''two-sided''' test, meaning that it tests for a significant difference between the observed and expected frequencies in both directions (i.e., either a greater than or less than difference). | |||
* [https://statsandr.com/blog/chi-square-test-of-independence-by-hand/ Chi-square test of independence by hand] | |||
<pre> | |||
> chisq.test(matrix(c(14,0,4,10), nr=2), correct=FALSE) | |||
Pearson's Chi-squared test | |||
data: matrix(c(14, 0, 4, 10), nr = 2) | |||
X-squared = 15.556, df = 1, p-value = 8.012e-05 | |||
# How about the case if expected=0 for some elements? | |||
> chisq.test(matrix(c(14,0,4,0), nr=2), correct=FALSE) | |||
Pearson's Chi-squared test | |||
data: matrix(c(14, 0, 4, 0), nr = 2) | |||
X-squared = NaN, df = 1, p-value = NA | |||
Warning message: | |||
In chisq.test(matrix(c(14, 0, 4, 0), nr = 2), correct = FALSE) : | |||
Chi-squared approximation may be incorrect | |||
</pre> | |||
[https://www.rdatagen.net/post/a-little-intuition-and-simulation-behind-the-chi-square-test-of-independence-part-2/ Exploring the underlying theory of the chi-square test through simulation - part 2] | |||
The result of Fisher exact test and chi-square test can be quite different. | |||
<pre> | |||
# https://myweb.uiowa.edu/pbreheny/7210/f15/notes/9-24.pdf#page=4 | |||
R> Job <- matrix(c(16,48,67,21,0,19,53,88), nr=2, byrow=T) | |||
R> dimnames(Job) <- list(A=letters[1:2],B=letters[1:4]) | |||
R> fisher.test(Job) | |||
Fisher's Exact Test for Count Data | |||
data: Job | |||
p-value < 2.2e-16 | |||
alternative hypothesis: two.sided | |||
R> chisq.test(c(16,48,67,21), c(0,19,53,88)) | |||
Pearson's Chi-squared test | |||
data: c(16, 48, 67, 21) and c(0, 19, 53, 88) | |||
X-squared = 12, df = 9, p-value = 0.2133 | |||
Warning message: | |||
In chisq.test(c(16, 48, 67, 21), c(0, 19, 53, 88)) : | |||
Chi-squared approximation may be incorrect | |||
</pre> | |||
== Cochran-Armitage test for trend (2xk) == | |||
* [https://en.wikipedia.org/wiki/Cochran%E2%80%93Armitage_test_for_trend Cochran–Armitage test for trend] | |||
* [https://search.r-project.org/CRAN/refmans/DescTools/html/CochranArmitageTest.html CochranArmitageTest()]. CochranArmitageTest(dose, alternative="one.sided") if dose is a 2xk or kx2 matrix. | |||
* [https://rdocumentation.org/packages/stats/versions/3.6.2/topics/prop.trend.test ?prop.trend.test]. prop.trend.test(dose[2,] , colSums(dose)) | |||
== PAsso: Partial Association between ordinal variables after adjustment == | |||
https://github.com/XiaoruiZhu/PAsso | |||
== Cochran-Mantel-Haenszel (CMH) & Association Tests for Ordinal Table == | |||
* [https://predictivehacks.com/contingency-tables-in-r/ Contingency Tables In R] | |||
* [https://rcompanion.org/handbook/H_09.html Association Tests for Ordinal Table] | |||
* [https://online.stat.psu.edu/stat504/lesson/5/5.3/5.3.5 5.3.5 - Cochran-Mantel-Haenszel Test] psu.edu | |||
* https://en.wikipedia.org/wiki/Cochran%E2%80%93Mantel%E2%80%93Haenszel_statistics | |||
== GSEA == | |||
See [[GSEA|GSEA]]. | |||
== McNemar’s test on paired nominal data == | |||
https://en.wikipedia.org/wiki/McNemar%27s_test | |||
== R == | |||
[https://predictivehacks.com/contingency-tables-in-r/ Contingency Tables In R]. Two-Way Tables, Mosaic plots, Proportions of the Contingency Tables, Rows and Columns Totals, Statistical Tests, Three-Way Tables, Cochran-Mantel-Haenszel (CMH) Methods. | |||
= Relationship between two variables = | |||
* [https://www.r-bloggers.com/2025/03/cor-function-in-r-calculate-correlation-coefficients-in-r/ cor Function in R] | |||
== Spearman vs Pearson correlation == | |||
Pearson benchmarks linear relationship, Spearman benchmarks monotonic relationship. https://stats.stackexchange.com/questions/8071/how-to-choose-between-pearson-and-spearman-correlation | |||
[https://en.wikipedia.org/wiki/Pearson_correlation_coefficient#Testing_using_Student's_t-distribution Testing using Student's t-distribution] cor.test() (T-distribution with n-1 d.f.). The normality assumption is used in test. For estimation, it affects the unbiased and efficiency. See [https://en.wikipedia.org/wiki/Pearson_correlation_coefficient#Sensitivity_to_the_data_distribution Sensitivity to the data distribution]. | |||
<pre> | |||
x=(1:100); | |||
y=exp(x); | |||
cor(x,y, method='spearman') # 1 | |||
cor(x,y, method='pearson') # .25 | |||
</pre> | |||
[https://stats.stackexchange.com/a/344758 How to know whether Pearson's or Spearman's correlation is better to use?] & | |||
[https://statisticsbyjim.com/basics/spearmans-correlation/ Spearman’s Correlation Explained]. Spearman's 𝜌 is better than Pearson correlation since | |||
* it doesn't assume linear relationship between variables | |||
* it is resistant to outliers | |||
* it handles ordinal data that are not interval-scaled | |||
== Spearman vs Wilcoxon == | |||
By [http://www.talkstats.com/threads/wilcoxon-signed-rank-test-or-spearmans-rho.42395/ this post] | |||
* Wilcoxon used to compare categorical versus non-normal continuous variable | |||
* Spearman's rho used to compare two continuous (including '''ordinal''') variables that one or both aren't normally distributed | |||
== Spearman vs [https://en.wikipedia.org/wiki/Kendall_rank_correlation_coefficient Kendall correlation] == | |||
* Kendall's tau coefficient (after the Greek letter τ), is a statistic used to measure the '''ordinal''' association between two measured quantities. | |||
* [https://statisticaloddsandends.wordpress.com/2019/07/08/spearmans-rho-and-kendalls-tau/ Spearman’s rho and Kendall’s tau] from Statistical Odds & Ends | |||
* [https://stats.stackexchange.com/questions/3943/kendall-tau-or-spearmans-rho Kendall Tau or Spearman's rho?] | |||
* [https://finnstats.com/index.php/2021/06/10/kendalls-rank-correlation-in-r-correlation-test/ Kendall’s Rank Correlation in R-Correlation Test] | |||
* Kendall’s tau is also '''more robust (less sensitive) to ties and outliers''' than Spearman’s rho. However, if the data are continuous or nearly so, Spearman’s rho may be more appropriate. | |||
* Kendall’s tau is preferred when dealing with '''small samples'''. [https://datascience.stackexchange.com/questions/64260/pearson-vs-spearman-vs-kendall Pearson vs Spearman vs Kendall]. | |||
* '''Interpretation of concordant and discordant pairs''': Kendall’s tau quantifies the difference between the percentage of concordant and discordant pairs among all possible pairwise events, which can be a more direct interpretation in certain contexts | |||
* Although Kendall’s tau has a higher computation complexity (O(n^2)) compared to Spearman’s rho (O(n logn)), it can still be preferred in certain scenarios. | |||
== Pearson/Spearman/Kendall correlations == | |||
* [https://www.r-bloggers.com/2023/09/pearson-spearman-and-kendall-correlation-coefficients-by-hand/ Calculate Pearson, Spearman and Kendall correlation coefficients by hand] | |||
* [https://datascience.stackexchange.com/questions/64260/pearson-vs-spearman-vs-kendall Pearson vs Spearman vs Kendall]. Formula in one page. | |||
* [https://ademos.people.uic.edu/Chapter22.html Chapter 22: Correlation Types and When to Use Them] from uic.edu | |||
== Jonckheere-Terpstra test == | |||
* [https://cran.r-project.org/web/packages/clinfun/clinfun.pdf#page=12 clinfun::jonckheere.test(x, group)] | |||
* The JT test is suitable if one variable is continuous and the other one is a variable with a natural ordering (e.g. independent groups such as drug dosages). If the other variable is like a continuous time variable, it would be better to use the Kendall test. | |||
== phi correlation for binary variables == | |||
https://en.wikipedia.org/wiki/Phi_coefficient. A Pearson correlation coefficient estimated for two binary variables will return the phi coefficient. | |||
<pre> | |||
set.seed(1) | |||
data <- data.frame(x=sample(c(0,1), 100, replace = T), y= sample(c(0,1), 100, replace = T)) | |||
cor(data$x, data$y) | |||
# [1] -0.03887781 | |||
library(psych) | |||
psych::phi(table(data$x, data$y)) | |||
# [1] -0.04 | |||
</pre> | |||
== The real meaning of spurious correlations == | |||
https://nsaunders.wordpress.com/2017/02/03/the-real-meaning-of-spurious-correlations/ | |||
{{Pre}} | |||
library(ggplot2) | |||
set.seed(123) | |||
spurious_data <- data.frame(x = rnorm(500, 10, 1), | |||
y = rnorm(500, 10, 1), | |||
z = rnorm(500, 30, 3)) | |||
cor(spurious_data$x, spurious_data$y) | |||
# [1] -0.05943856 | |||
spurious_data %>% ggplot(aes(x, y)) + geom_point(alpha = 0.3) + | |||
theme_bw() + labs(title = "Plot of y versus x for 500 observations with N(10, 1)") | |||
cor(spurious_data$x / spurious_data$z, spurious_data$y / spurious_data$z) | |||
# [1] 0.4517972 | |||
spurious_data %>% ggplot(aes(x/z, y/z)) + geom_point(aes(color = z), alpha = 0.5) + | |||
theme_bw() + geom_smooth(method = "lm") + | |||
scale_color_gradientn(colours = c("red", "white", "blue")) + | |||
labs(title = "Plot of y/z versus x/z for 500 observations with x,y N(10, 1); z N(30, 3)") | |||
spurious_data$z <- rnorm(500, 30, 6) | |||
cor(spurious_data$x / spurious_data$z, spurious_data$y / spurious_data$z) | |||
# [1] 0.8424597 | |||
spurious_data %>% ggplot(aes(x/z, y/z)) + geom_point(aes(color = z), alpha = 0.5) + | |||
theme_bw() + geom_smooth(method = "lm") + | |||
scale_color_gradientn(colours = c("red", "white", "blue")) + | |||
labs(title = "Plot of y/z versus x/z for 500 observations with x,y N(10, 1); z N(30, 6)") | |||
</pre> | |||
== A New Coefficient of Correlation == | |||
[https://towardsdatascience.com/a-new-coefficient-of-correlation-64ae4f260310 A New Coefficient of Correlation] Chatterjee, 2020 Jasa | |||
= Case control study = | |||
* See an example from the '''odds ratio''' calculation in https://en.wikipedia.org/wiki/Odds_ratio where it shows odds ratio can be calculated but '''relative risk''' cannot in the '''case-control study''' (useful in a rare-disease case). | |||
* https://www.statisticshowto.datasciencecentral.com/case-control-study/ | |||
* https://medical-dictionary.thefreedictionary.com/case-control+study | |||
* https://en.wikipedia.org/wiki/Case%E2%80%93control_study Cf. '''randomized controlled trial''', '''cohort study''' | |||
* https://www.students4bestevidence.net/blog/2017/12/06/case-control-and-cohort-studies-overview/ | |||
* https://quizlet.com/16214330/case-control-study-flash-cards/ | |||
= Confidence vs Credibility Intervals = | |||
http://freakonometrics.hypotheses.org/18117 | |||
== T-distribution vs normal distribution == | |||
* [https://www.statology.org/normal-distribution-vs-t-distribution/ Normal Distribution vs. t-Distribution: What’s the Difference?] | |||
* Test normal distribution | |||
<pre> | |||
set.seed(1); shapiro.test(rnorm(5000) ) | |||
# Shapiro-Wilk normality test | |||
# data: rnorm(5000) | |||
# W = 0.99957, p-value = 0.3352. --> accept H0 | |||
set.seed(1234567); shapiro.test(rnorm(5000) ) | |||
# Shapiro-Wilk normality test | |||
# data: rnorm(5000) | |||
# W = 0.99934, p-value = 0.06508 --> accept H0, but close to .05 | |||
</pre> | |||
= Power analysis/Sample Size determination = | |||
See [[Power|Power]]. | |||
= Common covariance/correlation structures = | |||
See [https://onlinecourses.science.psu.edu/stat502/node/228 psu.edu]. Assume covariance <math>\Sigma = (\sigma_{ij})_{p\times p} </math> | |||
* Diagonal structure: <math>\sigma_{ij} = 0</math> if <math>i \neq j</math>. | |||
* Compound symmetry: <math>\sigma_{ij} = \rho</math> if <math>i \neq j</math>. | |||
* First-order autoregressive AR(1) structure: <math>\sigma_{ij} = \rho^{|i - j|}</math>. <syntaxhighlight lang='rsplus'> | |||
rho <- .8 | rho <- .8 | ||
p <- 5 | p <- 5 | ||
blockMat <- rho ^ abs(matrix(1:p, p, p, byrow=T) - matrix(1:p, p, p)) | blockMat <- rho ^ abs(matrix(1:p, p, p, byrow=T) - matrix(1:p, p, p)) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
* Banded matrix: <math>\sigma_{ii}=1, \sigma_{i,i+1}=\sigma_{i+1,i} \neq 0, \sigma_{i,i+2}=\sigma_{i+2,i} \neq 0</math> and <math>\sigma_{ij}=0</math> for <math>|i-j| \ge 3</math>. | * Banded matrix: <math>\sigma_{ii}=1, \sigma_{i,i+1}=\sigma_{i+1,i} \neq 0, \sigma_{i,i+2}=\sigma_{i+2,i} \neq 0</math> and <math>\sigma_{ij}=0</math> for <math>|i-j| \ge 3</math>. | ||
* Spatial Power | * Spatial Power | ||
* Unstructured Covariance | * Unstructured Covariance | ||
* [https://en.wikipedia.org/wiki/Toeplitz_matrix Toeplitz structure] | * [https://en.wikipedia.org/wiki/Toeplitz_matrix Toeplitz structure] | ||
To create blocks of correlation matrix, use the "%x%" operator. See [https://www.rdocumentation.org/packages/base/versions/3.4.3/topics/kronecker kronecker()]. | To create blocks of correlation matrix, use the "%x%" operator. See [https://www.rdocumentation.org/packages/base/versions/3.4.3/topics/kronecker kronecker()]. | ||
{{Pre}} | {{Pre}} | ||
covMat <- diag(n.blocks) %x% blockMat | covMat <- diag(n.blocks) %x% blockMat | ||
</pre> | </pre> | ||
= Counter/Special Examples = | |||
* [https://www.tandfonline.com/doi/full/10.1080/00031305.2021.2004922 Myths About Linear and Monotonic Associations: Pearson’s r, Spearman’s ρ, and Kendall’s τ] van den Heuvel 2022 | |||
= | == Math myths == | ||
[https:// | * [https://twitter.com/mathladyhazel/status/1557225372890152960 How 1+2+3+4+5+6+7+..... equals a negative number! ] S=-1/8 | ||
* [https://en.wikipedia.org/wiki/1_+_2_+_3_+_4_+_%E2%8B%AF 1 + 2 + 3 + 4 + ⋯ = -1/12] | |||
== Correlated does not imply independence == | == Correlated does not imply independence == | ||
| Line 2,082: | Line 2,894: | ||
This example shows how a linear correlation coefficient does not encapsulate anything about the quadratic dependence of Y upon X. | This example shows how a linear correlation coefficient does not encapsulate anything about the quadratic dependence of Y upon X. | ||
== | == Significant p value but no correlation == | ||
[https://stats.stackexchange.com/a/333752 Post] where p-value = 1.18e-06 but cor=0.067. p-value does not say anything about the size of r. | |||
cor | |||
== [http://en.wikipedia.org/wiki/Anscombe%27s_quartet Anscombe quartet] == | == [http://en.wikipedia.org/wiki/Anscombe%27s_quartet Anscombe quartet] == | ||
| Line 2,107: | Line 2,902: | ||
[[:File:Anscombe quartet 3.svg]] | [[:File:Anscombe quartet 3.svg]] | ||
= Time series = | = Time series = | ||
| Line 2,162: | Line 2,927: | ||
= Statistical guidance = | = Statistical guidance = | ||
[https://osf.io/preprints/metaarxiv/q6ajt Statistical guidance to authors at top-ranked scientific journals: A cross-disciplinary assessment] | * [https://osf.io/preprints/metaarxiv/q6ajt Statistical guidance to authors at top-ranked scientific journals: A cross-disciplinary assessment] | ||
* [https://www.youtube.com/watch?v=iu4VsEv1WIo How to get your article rejected by the BMJ: 12 common statistical issues] Richard Riley | |||
= Books, learning material = | = Books, learning material = | ||
* [https://annas-archive.org/ Anna’s Archive] | |||
* [https://leanpub.com/biostatmethods Methods in Biostatistics with R] ($) | * [https://leanpub.com/biostatmethods Methods in Biostatistics with R] ($) | ||
* [http://web.stanford.edu/class/bios221/book/ Modern Statistics for Modern Biology] (free) | * [http://web.stanford.edu/class/bios221/book/ Modern Statistics for Modern Biology] (free) | ||
| Line 2,172: | Line 2,939: | ||
* [https://web.stanford.edu/~hastie/CASI/ Computer Age Statistical Inference: Algorithms, Evidence and Data Science] by Efron and Hastie 2016 | * [https://web.stanford.edu/~hastie/CASI/ Computer Age Statistical Inference: Algorithms, Evidence and Data Science] by Efron and Hastie 2016 | ||
* [https://si.biostat.washington.edu/suminst/sisg2020/modules UW Biostatistics Summer Courses] (4 institutes) | * [https://si.biostat.washington.edu/suminst/sisg2020/modules UW Biostatistics Summer Courses] (4 institutes) | ||
* [https://www.springer.com/series/2848/books Statistics for Biology and Health] Springer. | |||
* [https://pyoflife.com/bayesian-essentials-with-r/ Bayesian Essentials with R] | |||
* [https://www.maths.ed.ac.uk/~swood34/core-statistics.pdf Core Statistics] Simon Wood | |||
= Social = | = Social = | ||
Latest revision as of 14:18, 22 December 2025
Statisticians
- Karl Pearson (1857-1936): chi-square, p-value, PCA
- William Sealy Gosset (1876-1937): Student's t
- Ronald Fisher (1890-1962): ANOVA
- Egon Pearson (1895-1980): son of Karl Pearson
- Jerzy Neyman (1894-1981): type 1 error
- Ten Statistical Ideas that Changed the World
The most important statistical ideas of the past 50 years
What are the most important statistical ideas of the past 50 years?, JASA 2021
Some Advice
- Statistics for biologists
- On the 12th Day of Christmas, a Statistician Sent to Me . . ., The abridged 1-page print version.
Data
Rules for initial data analysis
Ten simple rules for initial data analysis
Types of probabilities
See this illustration
Exploratory Analysis (EDA)
- Kmeans Clustering of Penguins
- skimr package
- dataxray package - An interactive table interface (of skimr) for data summaries. Cut your EDA time into 5 minutes with Exploratory DataXray Analysis (EDXA)
- 20 Useful R Packages You May Not Know Of
- 12 guidelines for data exploration and analysis with the right attitude for discovery
Kurtosis
Kurtosis in R-What do you understand by Kurtosis?
Phi coefficient
- Phi coefficient. Its values is [-1, 1]. A value of zero means that the binary variables are not positively or negatively associated.
- How to Calculate Phi Coefficient in R. It is a measurement of the degree of association between two binary variables.
- Cramér’s V. Its value is [0, 1]. A value of zero indicates that there is no association between the two variables. This means that knowing the value of one variable does not help predict the value of the other variable.
library(vcd) cramersV <- assocstats(table(x, y))$cramer
Coefficient of variation (CV)
Motivating the coefficient of variation (CV) for beginners:
- Boss: Measure it 5 times.
- You: 8, 8, 9, 6, and 8
- B: SD=1. Make it three times more precise!
- Y: 0.20 0.20 0.23 0.15 0.20 meters. SD=0.3!
- B: All you did was change to meters! Report the CV instead!
- Y: Damn it.
R> sd(c(8, 8, 9, 6, 8)) [1] 1.095445 R> sd(c(8, 8, 9, 6, 8)*2.54/100) [1] 0.02782431
Agreement
Pitfalls
Common pitfalls in statistical analysis: Measures of agreement 2017
Cohen's Kappa statistic (2-class)
- Cohen's kappa. Cohen's kappa measures the agreement between two raters who each classify N items into C mutually exclusive categories.
- Fleiss kappa vs Cohen kappa.
- Cohen’s kappa is calculated based on the confusion matrix. However, in contrast to calculating overall accuracy, Cohen’s kappa takes imbalance in class distribution into account and can therefore be more complex to interpret.
Fleiss Kappa statistic (more than two raters)
- https://en.wikipedia.org/wiki/Fleiss%27_kappa
- Fleiss kappa (more than two raters) to test interrater reliability or to evaluate the repeatability and stability of models (robustness). This was used by Cancer prognosis prediction of Zheng 2020. "In our case, each trained model is designed to be a rater to assign the affiliation of each variable (gene or pathway). We conducted 20 replications of fivefold cross validation. As such, we had 100 trained models, or 100 raters in total, among which the agreement was measured by the Fleiss kappa..."
- Fleiss’ Kappa in R: For Multiple Categorical Variables. irr::kappam.fleiss() was used.
- Kappa statistic vs ICC
- ICC and Kappa totally disagree
- Measures of Interrater Agreement by Mandrekar 2011. "In certain clinical studies, agreement between the raters is assessed for a clinical outcome that is measured on a continuous scale. In such instances, intraclass correlation is calculated as a measure of agreement between the raters. Intraclass correlation is equivalent to weighted kappa under certain conditions, see the study by Fleiss and Cohen6, 7 for details."
ICC: intra-class correlation
See ICC
Compare two sets of p-values
https://stats.stackexchange.com/q/155407
Computing different kinds of correlations
correlation package
Partial correlation
Association is not causation
- Correlation Does Not Imply Causation: 5 Real-World Examples
- Spurious Correlations in R – Correlation is not Causation
- Reasons Why Correlation Does Not Imply Causation
- Third-Variable Problem: There may be an unseen third variable that is influencing both correlated variables. For example, ice cream sales and drowning incidents might be correlated because both increase during the summer, but neither causes the other.
- Reverse Causation: The direction of cause and effect might be opposite to what we assume. For example, one might assume that stress causes poor health (which it can), but it’s also possible that poor health increases stress.
- Coincidence: Sometimes, correlations occur purely by chance, especially if the sample size is large or if many variables are tested.
- Complex Interactions: The relationship between variables can be influenced by a complex interplay of multiple factors that correlation alone cannot unpack.
- Examples
- Example of Correlation without Causation: There is a correlation between the number of fire trucks at a fire scene and the amount of damage caused by the fire. However, this does not mean that the fire trucks cause the damage; rather, larger fires both require more fire trucks and cause more damage.
- Example of Potential Misinterpretation: Studies might find a correlation between coffee consumption and heart disease. Without further investigation, one might mistakenly conclude that drinking coffee causes heart disease. However, it could be that people who drink a lot of coffee are more likely to smoke, and smoking is the actual cause of heart disease.
- What People Are Getting Wrong This Week (and Every Week): Correlation and Causation
Predictive power score
Transform sample values to their percentiles
- ecdf()
- quantile()
- An example from the TreatmentSelection package where "type = 1" was used.
R> x <- c(1,2,3,4,4.5,6,7) R> Fn <- ecdf(x) R> Fn # a *function* Empirical CDF Call: ecdf(x) x[1:7] = 1, 2, 3, ..., 6, 7 R> Fn(x) # returns the percentiles for x [1] 0.1428571 0.2857143 0.4285714 0.5714286 0.7142857 0.8571429 1.0000000 R> diff(Fn(x)) [1] 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 0.1428571 R> quantile(x, Fn(x)) 14.28571% 28.57143% 42.85714% 57.14286% 71.42857% 85.71429% 100% 1.857143 2.714286 3.571429 4.214286 4.928571 6.142857 7.000000 R> quantile(x, Fn(x), type = 1) 14.28571% 28.57143% 42.85714% 57.14286% 71.42857% 85.71429% 100% 1.0 2.0 3.0 4.0 4.5 6.0 7.0 R> x <- c(2, 6, 8, 10, 20) R> Fn <- ecdf(x) R> Fn(x) [1] 0.2 0.4 0.6 0.8 1.0 - Definition of a Percentile in Statistics and How to Calculate It
- https://en.wikipedia.org/wiki/Percentile
- Percentile vs. Quartile vs. Quantile: What’s the Difference?
- Percentiles: Range from 0 to 100.
- Quartiles: Range from 0 to 4.
- Quantiles: Range from any value to any other value.
Standardization
Feature standardization considered harmful
Eleven quick tips for finding research data
http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1006038
An archive of 1000+ datasets distributed with R
https://vincentarelbundock.github.io/Rdatasets/
Data and global
- Age Structure from One Data in World. Our World in Data is a non-profit organization that provides free and open access to data and insights on how the world is changing across 115 topics.
Box(Box, whisker & outlier)
- https://en.wikipedia.org/wiki/Box_plot, Boxplot and a probability density function (pdf) of a Normal Population for a good annotation.
- https://owi.usgs.gov/blog/boxplots/ (ggplot2 is used, graph-assisting explanation)
- https://flowingdata.com/2008/02/15/how-to-read-and-use-a-box-and-whisker-plot/
- Quartile from Wikipedia. The quartiles returned from R are the same as the method defined by Method 2 described in Wikipedia.
- How to make a boxplot in R. The whiskers of a box and whisker plot are the dotted lines outside of the grey box. These end at the minimum and maximum values of your data set, excluding outliers.
An example for a graphical explanation. File:Boxplot.svg, File:Geom boxplot.png
> x=c(0,4,15, 1, 6, 3, 20, 5, 8, 1, 3)
> summary(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0 2 4 6 7 20
> sort(x)
[1] 0 1 1 3 3 4 5 6 8 15 20
> y <- boxplot(x, col = 'grey')
> t(y$stats)
[,1] [,2] [,3] [,4] [,5]
[1,] 0 2 4 7 8
# the extreme of the lower whisker, the lower hinge, the median,
# the upper hinge and the extreme of the upper whisker
# https://en.wikipedia.org/wiki/Quartile#Example_1
> summary(c(6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49))
Min. 1st Qu. Median Mean 3rd Qu. Max.
6.00 25.50 40.00 33.18 42.50 49.00
- The lower and upper edges of box (also called the lower/upper hinge) is determined by the first and 3rd quartiles (2 and 7 in the above example).
- 2 = median(c(0, 1, 1, 3, 3, 4)) = (1+3)/2
- 7 = median(c(4, 5, 6, 8, 15, 20)) = (6+8)/2
- IQR = 7 - 2 = 5
- The thick dark horizon line is the median (4 in the example).
- Outliers are defined by (the empty circles in the plot)
- Observations larger than 3rd quartile + 1.5 * IQR (7+1.5*5=14.5) and
- smaller than 1st quartile - 1.5 * IQR (2-1.5*5=-5.5).
- Note that the cutoffs are not shown in the Box plot.
- Whisker (defined using the cutoffs used to define outliers)
- Upper whisker is defined by the largest "data" below 3rd quartile + 1.5 * IQR (8 in this example). Note Upper whisker is NOT defined as 3rd quartile + 1.5 * IQR.
- Lower whisker is defined by the smallest "data" greater than 1st quartile - 1.5 * IQR (0 in this example). Note lower whisker is NOT defined as 1st quartile - 1.5 * IQR.
- See another example below where we can see the whiskers fall on observations.
- Some software like GraphPad has multiple ways to draw whiskers, e.g., 5 and 95 percentiles. See Five ways to plot whiskers in box and whisker plots.
Note the wikipedia lists several possible definitions of a whisker. R uses the 2nd method (Tukey boxplot) to define whiskers.
Create boxplots from a list object
Normally we use a vector to create a single boxplot or a formula on a data to create boxplots.
But we can also use split() to create a list and then make boxplots.
Dot-box plot
- http://civilstat.com/2012/09/the-grammar-of-graphics-notes-on-first-reading/
- http://www.r-graph-gallery.com/89-box-and-scatter-plot-with-ggplot2/
- http://www.sthda.com/english/wiki/ggplot2-box-plot-quick-start-guide-r-software-and-data-visualization
- Graphs in R – Overlaying Data Summaries in Dotplots. Note that for some reason, the boxplot will cover the dots when we save the plot to an svg or a png file. So an alternative solution is to change the order
par(cex.main=0.9,cex.lab=0.8,font.lab=2,cex.axis=0.8,font.axis=2,col.axis="grey50") boxplot(weight ~ feed, data = chickwts, range=0, whisklty = 0, staplelty = 0) par(new = TRUE) stripchart(weight ~ feed, data = chickwts, xlim=c(0.5,6.5), vertical=TRUE, method="stack", offset=0.8, pch=19, main = "Chicken weights after six weeks", xlab = "Feed Type", ylab = "Weight (g)")
geom_boxplot
Note the geom_boxplot() does not create crossbars. See How to generate a boxplot graph with whisker by ggplot or this. A trick is to add the stat_boxplot() function.
Without jitter
ggplot(dfbox, aes(x=sample, y=expr)) +
geom_boxplot() +
theme(axis.text.x=element_text(color = "black", angle=30, vjust=.8,
hjust=0.8, size=6),
plot.title = element_text(hjust = 0.5)) +
labs(title="", y = "", x = "")
With jitter
ggplot(dfbox, aes(x=sample, y=expr)) +
geom_boxplot(outlier.shape=NA) + #avoid plotting outliers twice
geom_jitter(position=position_jitter(width=.2, height=0)) +
theme(axis.text.x=element_text(color = "black", angle=30, vjust=.8,
hjust=0.8, size=6),
plot.title = element_text(hjust = 0.5)) +
labs(title="", y = "", x = "")
Why geom_boxplot identify more outliers than base boxplot?
What do hjust and vjust do when making a plot using ggplot? The value of hjust and vjust are only defined between 0 and 1: 0 means left-justified, 1 means right-justified.
Other boxplots
Annotated boxplot
https://stackoverflow.com/a/38032281
Outliers in data analysis
Outliers in Data Analysis: Detecting Extreme Values Before Modeling in R with İstanbul Airbnb Data
stem and leaf plot
stem(). See R Tutorial.
Note that stem plot is useful when there are outliers.
> stem(x) The decimal point is 10 digit(s) to the right of the | 0 | 00000000000000000000000000000000000000000000000000000000000000000000+419 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 9 > max(x) [1] 129243100275 > max(x)/1e10 [1] 12.92431 > stem(y) The decimal point is at the | 0 | 014478 1 | 0 2 | 1 3 | 9 4 | 8 > y [1] 3.8667356428 0.0001762708 0.7993462430 0.4181079732 0.9541728562 [6] 4.7791262101 0.6899313108 2.1381289177 0.0541736818 0.3868776083 > set.seed(1234) > z <- rnorm(10)*10 > z [1] -12.070657 2.774292 10.844412 -23.456977 4.291247 5.060559 [7] -5.747400 -5.466319 -5.644520 -8.900378 > stem(z) The decimal point is 1 digit(s) to the right of the | -2 | 3 -1 | 2 -0 | 9665 0 | 345 1 | 1
Box-Cox transformation
CLT/Central limit theorem
Delta method
Sample median, x-percentiles
- Central limit theorem for sample medians
- For the q-th sample quantile in sufficiently large samples, we get that it will approximately have a normal distribution with mean the [math]\displaystyle{ 𝑞 }[/math]th population quantile [math]\displaystyle{ 𝑥_𝑞 }[/math] and variance [math]\displaystyle{ 𝑞(1−𝑞)/(𝑛𝑓_𝑋(𝑥_𝑞)^2) }[/math]. Hence for the median (𝑞=1/2), the variance in sufficiently large samples will be approximately [math]\displaystyle{ 1/(4𝑛𝑓_𝑋(m)^2) }[/math].
- For example for an exponential distribution with a rate parameter [math]\displaystyle{ \lambda \gt 0 }[/math], the pdf is [math]\displaystyle{ f(x)=\lambda \exp(-\lambda x) }[/math]. The population median [math]\displaystyle{ m }[/math] is the value such as [math]\displaystyle{ F(m)=.5 }[/math]. So [math]\displaystyle{ m=log(2)/\lambda }[/math]. For large n, the sample median [math]\displaystyle{ \tilde{X} }[/math] will be approximately normal distributed around the population median [math]\displaystyle{ m }[/math], but with the asymptotic variance given by [math]\displaystyle{ Var(\tilde{X}) \approx \frac{1}{4nf(m)^2} }[/math] where [math]\displaystyle{ f(m) }[/math] is the PDF evaluated at the median [math]\displaystyle{ m=\log(2)/\lambda }[/math]. For the exponential distribution with rate [math]\displaystyle{ \lambda }[/math], we have [math]\displaystyle{ f(m) = \lambda e^{-\lambda m} = \lambda/2 }[/math]. Substituting this into the expression for the variance we have [math]\displaystyle{ Var(\tilde{X}) \approx \frac{1}{n\lambda^2} }[/math].
- For normal distribution with mean [math]\displaystyle{ \mu }[/math] and variance [math]\displaystyle{ \sigma^2 }[/math]. The sample median has a limiting distribution of normal with mean [math]\displaystyle{ \mu }[/math] and variance [math]\displaystyle{ \frac{1}{4nf(m)^2} = \frac{\pi \sigma^2}{2n} }[/math].
- Some references:
- "Mathematical Statistics" by Jun Shao
- "Probability and Statistics" by DeGroot and Schervish
- "Order Statistics" by H.A. David and H.N. Nagaraja
the Holy Trinity (LRT, Wald, Score tests)
- https://en.wikipedia.org/wiki/Likelihood_function which includes profile likelihood and partial likelihood
- Review of the likelihood theory
- The “Three Plus One” Likelihood-Based Test Statistics: Unified Geometrical and Graphical Interpretations
- Variable selection – A review and recommendations for the practicing statistician by Heinze et al 2018.
- Score test is step-up. Score test is typically used in forward steps to screen covariates currently not included in a model for their ability to improve model.
- Wald test is step-down. Wald test starts at the full model. It evaluate the significance of a variable by comparing the ratio of its estimate and its standard error with an appropriate T distribution (for linear models) or standard normal distribution (for logistic or Cox regression).
- Likelihood ratio tests provide the best control over nuisance parameters by maximizing the likelihood over them both in H0 model and H1 model. In particular, if several coefficients are being tested simultaneously, LRTs for model comparison are preferred over Wald or score tests.
- R packages
- lmtest package, waldtest() and lrtest(). Likelihood Ratio Test in R with Example
- aod package. How to Perform a Wald Test in R
- survey package. regTermTest()
- nlWaldTest package.
- Likelihood ratio test multiplying by 2. Hint: Approximate the log-likelihood for the true value of the parameter using the Taylor expansion around the MLE.
- Wald statistic relationship to Z-statistic: The Wald statistic is essentially the square of the Z-statistic. In other words, a Wald statistic is computed as Z squared. However, there is a key difference in the denominator of these statistics: the Z-statistic uses the null standard error (calculated using the hypothesized value), while the Wald statistic uses the standard error evaluated at the maximum likelihood estimate.
Don't invert that matrix
- http://www.johndcook.com/blog/2010/01/19/dont-invert-that-matrix/
- http://civilstat.com/2015/07/dont-invert-that-matrix-why-and-how/
Different matrix decompositions/factorizations
- QR decomposition, qr()
- LU decomposition, lu() from the 'Matrix' package
- Cholesky decomposition, chol()
- Singular value decomposition, svd()
set.seed(1234) x <- matrix(rnorm(10*2), nr= 10) cmat <- cov(x); cmat # [,1] [,2] # [1,] 0.9915928 -0.1862983 # [2,] -0.1862983 1.1392095 # cholesky decom d1 <- chol(cmat) t(d1) %*% d1 # equal to cmat d1 # upper triangle # [,1] [,2] # [1,] 0.9957875 -0.1870864 # [2,] 0.0000000 1.0508131 # svd d2 <- svd(cmat) d2$u %*% diag(d2$d) %*% t(d2$v) # equal to cmat d2$u %*% diag(sqrt(d2$d)) # [,1] [,2] # [1,] -0.6322816 0.7692937 # [2,] 0.9305953 0.5226872
Model Estimation with R
Model Estimation by Example Demonstrations with R. Michael Clark
Regression
Non- and semi-parametric regression
- Semiparametric Regression in R
- https://socialsciences.mcmaster.ca/jfox/Courses/Oxford-2005/R-nonparametric-regression.html
Mean squared error
- Simulating the bias-variance tradeoff in R
- Estimating variance: should I use n or n - 1? The answer is not what you think
Brier score
- https://en.wikipedia.org/wiki/Brier_score (it was proposed by Glenn W. Brier in 1950)
- It seems Brier Score and Mean Squared error have the same formula.
- Brier score seems to be applied to binary or category outcome (prediction is probabilities in [0,1]) while mean squared error is applied to continuous value outcome (prediction is numeric values).
Splines
- https://en.wikipedia.org/wiki/B-spline
- Cubic and Smoothing Splines in R. bs() is for cubic spline and smooth.spline() is for smoothing spline.
- Can we use B-splines to generate non-linear data?
- How to force passing two data points? (cobs package)
- https://www.rdocumentation.org/packages/cobs/versions/1.3-3/topics/cobs
k-Nearest neighbor regression
- class::knn()
- k-NN regression in practice: boundary problem, discontinuities problem.
- Weighted k-NN regression: want weight to be small when distance is large. Common choices - weight = kernel(xi, x)
Kernel regression
- Instead of weighting NN, weight ALL points. Nadaraya-Watson kernel weighted average:
[math]\displaystyle{ \hat{y}_q = \sum c_{qi} y_i/\sum c_{qi} = \frac{\sum \text{Kernel}_\lambda(\text{distance}(x_i, x_q))*y_i}{\sum \text{Kernel}_\lambda(\text{distance}(x_i, x_q))} }[/math].
- Choice of bandwidth [math]\displaystyle{ \lambda }[/math] for bias, variance trade-off. Small [math]\displaystyle{ \lambda }[/math] is over-fitting. Large [math]\displaystyle{ \lambda }[/math] can get an over-smoothed fit. Cross-validation.
- Kernel regression leads to locally constant fit.
- Issues with high dimensions, data scarcity and computational complexity.
Principal component analysis
See PCA.
Partial Least Squares (PLS) regression
- Accounting for measurement errors with total least squares. Demonstrate the bias of the PLS.
- https://en.wikipedia.org/wiki/Partial_least_squares_regression. The general underlying model of multivariate PLS is
- [math]\displaystyle{ X = T P^\mathrm{T} + E }[/math]
- [math]\displaystyle{ Y = U Q^\mathrm{T} + F }[/math]
- where X is an [math]\displaystyle{ n \times m }[/math] matrix of predictors, Y is an [math]\displaystyle{ n \times p }[/math] matrix of responses; T and U are [math]\displaystyle{ n \times l }[/math] matrices that are, respectively, projections of X (the X score, component or factor matrix) and projections of Y (the Y scores); P and Q are, respectively, [math]\displaystyle{ m \times l }[/math] and [math]\displaystyle{ p \times l }[/math] orthogonal loading matrices; and matrices E and F are the error terms, assumed to be independent and identically distributed random normal variables. The decompositions of X and Y are made so as to maximise the covariance between T and U (projection matrices).
- Supervised vs. Unsupervised Learning: Exploring Brexit with PLS and PCA
- pls R package
- plsRcox R package (archived). See here for the installation.
- PLS, PCR (principal components regression) and ridge regression tend to behave similarly. Ridge regression may be preferred because it shrinks smoothly, rather than in discrete steps.
- So you think you can PLS-DA?. Compare PLS with PCA.
- plsRglm package - Partial Least Squares Regression for Generalized Linear Models
Partial Least Squares Discriminant Analysis (PLS-DA)
- Partial least squares discriminant analysis (PLS-DA) is a variant used when the Y is categorical.
- mixOmics package.
- Application: Comprehensive analysis of the cerebrospinal fluid and serum metabolome in neurological diseases.
High dimension
- Partial least squares prediction in high-dimensional regression Cook and Forzani, 2019
- High dimensional precision medicine from patient-derived xenografts JASA 2020
dimRed package
dimRed package
Feature selection
- https://en.wikipedia.org/wiki/Feature_selection
- A Feature Preprocessing Workflow
- Model-Free Feature Screening and FDR Control With Knockoff Features and pdf. The proposed method is based on the projection correlation which measures the dependence between two random vectors.
Goodness-of-fit
- A simple yet powerful test for assessing goodness‐of‐fit of high‐dimensional linear models Zhang 2021
- Pearson's goodness-of-fit tests for sparse distributions Chang 2021
Independent component analysis
ICA is another dimensionality reduction method.
ICA vs PCA
ICS vs FA
Robust independent component analysis
robustica: customizable robust independent component analysis 2022
Canonical correlation analysis
- https://en.wikipedia.org/wiki/Canonical_correlation. If we have two vectors X = (X1, ..., Xn) and Y = (Y1, ..., Ym) of random variables, and there are correlations among the variables, then canonical-correlation analysis will find linear combinations of X and Y which have maximum correlation with each other.
- R data analysis examples
- Canonical Correlation Analysis from psu.edu
- see the cancor function in base R; canocor in the calibrate package; and the CCA package.
- Introduction to Canonical Correlation Analysis (CCA) in R
Non-negative CCA
- https://cran.r-project.org/web/packages/nscancor/
- Pan-Cancer Analysis for Immune Cell Infiltration and Mutational Signatures Using Non-Negative Canonical Correlation Analysis 2022. Non-negative constraints that force all input elements and coefficients to be zero or positive values.
Correspondence analysis
- Relationship of PCA and Correspondence analysis
- CA - Correspondence Analysis in R: Essentials
- Understanding the Math of Correspondence Analysis, How to Interpret Correspondence Analysis Plots
- https://francoishusson.wordpress.com/2017/07/18/multiple-correspondence-analysis-with-factominer/ and the book Exploratory Multivariate Analysis by Example Using R
Non-negative matrix factorization
Optimization and expansion of non-negative matrix factorization
Nonlinear dimension reduction
- The Specious Art of Single-Cell Genomics by Chari 2021
polarisR package
polarisR. A 'shiny' application for visualizing high-dimensional data using non-linear dimensionality reduction (NLDR) techniques such as t-SNE and UMAP. It provides an interactive platform to explore high-dimensional datasets, diagnose the quality of the embeddings using the 'quollr' package, and compare different NLDR methods.
t-SNE
t-Distributed Stochastic Neighbor Embedding (t-SNE) is a technique for dimensionality reduction that is particularly well suited for the visualization of high-dimensional datasets.
- Wikipedia
- StatQuest: t-SNE, Clearly Explained
- https://lvdmaaten.github.io/tsne/
- Workshop: Dimension reduction with R Saskia Freytag
- Application to ARCHS4
- Visualization of High Dimensional Data using t-SNE with R
- http://blog.thegrandlocus.com/2018/08/a-tutorial-on-t-sne-1
- Quick and easy t-SNE analysis in R. M3C package was used.
- Visualization of Single Cell RNA-Seq Data Using t-SNE in R. Seurat (both Seurat and M3C call Rtsne) package was used.
- The art of using t-SNE for single-cell transcriptomics
- Normalization Methods on Single-Cell RNA-seq Data: An Empirical Survey
- An R package for t-SNE (pure R implementation)
- Understanding UMAP by Andy Coenen, Adam Pearce. Note that the Fashion MNIST data was used to explain what a global structure means (it means similar categories (such as sandal, sneaker, and ankle boot)).
- Hyperparameters really matter
- Cluster sizes in a UMAP plot mean nothing
- Distances between clusters might not mean anything
- Random noise doesn’t always look random.
- You may need more than one plot
Perplexity parameter
- Balance attention between local and global aspects of the dataset
- A guess about the number of close neighbors
- In a real setting is important to try different values
- Must be lower than the number of input records
- Interactive t-SNE ? Online. We see in addition to perplexity there are learning rate and max iterations.
Classifying digits with t-SNE: MNIST data
Below is an example from datacamp Advanced Dimensionality Reduction in R.
The mnist_sample is very small 200x785. Here (Exploring handwritten digit classification: a tidy analysis of the MNIST dataset) is a large data with 60k records (60000 x 785).
- Generating t-SNE features
library(readr) library(dplyr) # 104MB mnist_raw <- read_csv("https://pjreddie.com/media/files/mnist_train.csv", col_names = FALSE) mnist_10k <- mnist_raw[1:10000, ] colnames(mnist_10k) <- c("label", paste0("pixel", 0:783)) library(ggplot2) library(Rtsne) tsne <- Rtsne(mnist_10k[, -1], perplexity = 5) tsne_plot <- data.frame(tsne_x= tsne$Y[1:5000,1], tsne_y = tsne$Y[1:5000,2], digit = as.factor(mnist_10k[1:5000,]$label)) # visualize obtained embedding ggplot(tsne_plot, aes(x= tsne_x, y = tsne_y, color = digit)) + ggtitle("MNIST embedding of the first 5K digits") + geom_text(aes(label = digit)) + theme(legend.position= "none") - Computing centroids
library(data.table) # Get t-SNE coordinates centroids <- as.data.table(tsne$Y[1:5000,]) setnames(centroids, c("X", "Y")) centroids[, label := as.factor(mnist_10k[1:5000,]$label)] # Compute centroids centroids[, mean_X := mean(X), by = label] centroids[, mean_Y := mean(Y), by = label] centroids <- unique(centroids, by = "label") # visualize centroids ggplot(centroids, aes(x= mean_X, y = mean_Y, color = label)) + ggtitle("Centroids coordinates") + geom_text(aes(label = label)) + theme(legend.position = "none") - Classifying new digits
# Get new examples of digits 4 and 9 distances <- as.data.table(tsne$Y[5001:10000,]) setnames(distances, c("X" , "Y")) distances[, label := mnist_10k[5001:10000,]$label] distances <- distances[label == 4 | label == 9] # Compute the distance to the centroids distances[, dist_4 := sqrt(((X - centroids[label==4,]$mean_X) + (Y - centroids[label==4,]$mean_Y))^2)] dim(distances) # [1] 928 4 distances[1:3, ] # X Y label dist_4 # 1: -15.90171 27.62270 4 1.494578 # 2: -33.66668 35.69753 9 8.195562 # 3: -16.55037 18.64792 9 8.128860 # Plot distance to each centroid ggplot(distances, aes(x=dist_4, fill = as.factor(label))) + geom_histogram(binwidth=5, alpha=.5, position="identity", show.legend = F)
Fashion MNIST data
- fashion_mnist is only 500x785
- keras has 60k x 785. Miniconda is required when we want to use the package.
tSNE vs PCA
- PCA vs t-SNE: which one should you use for visualization. This uses MNIST dataset for a comparison.
- Why PCA on bulk RNA-Seq and t-SNE on scRNA-Seq?
- What to use: PCA or tSNE dimension reduction in DESeq2 analysis? (with discussion)
- Are there cases where PCA is more suitable than t-SNE?
- How to interpret data not separated by PCA but by T-sne/UMAP
- Dimensionality Reduction for Data Visualization: PCA vs TSNE vs UMAP vs LDA
Two groups example
suppressPackageStartupMessages({
library(splatter)
library(scater)
})
sim.groups <- splatSimulate(group.prob = c(0.5, 0.5), method = "groups",
verbose = FALSE)
sim.groups <- logNormCounts(sim.groups)
sim.groups <- runPCA(sim.groups)
plotPCA(sim.groups, colour_by = "Group") # 2 groups separated in PC1
sim.groups <- runTSNE(sim.groups)
plotTSNE(sim.groups, colour_by = "Group") # 2 groups separated in TSNE2
UMAP
- Uniform manifold approximation and projection
- UMAP creates a low-dimensional map that preserves local similarity relationships in high-dimensional data, allowing humans to visualize complex biological structure without using the map itself for classification or decision-making.
- Properties:
- Non-linear
- Preserves neighborhood structure/Local structure (vs PCA preserves variance). Points close together → similar profiles. Both UMAP and t-SNE are designed to preserve local structure.
- Stochastic (unless seeded)
- Gaps do not imply real biological distance
- Visual bias: UMAP appears more “continuous” but still distorts space. t-SNE exaggerates separation.
- Techniques for Visualizing High Dimensional Data
- good at displaying both global and local structure.
- Because of its speed, it's ideal for big datasets.
- t-sne was invented in 2008 and umap was 2018.
- https://cran.r-project.org/web/packages/uwot/index.html (more popular than the umap package)
- There is no official "backronym" for uwot in the documentation. In the R community, it is generally understood to be a play on the British/internet slang "U wat?" (as in "You what?").
- Install on macOS/Linux requires compilation.
- (macOS) First install gfortran by downloading gfortran from https://mac.r-project.org/tools/. The installer said The resulting compiler will live in /opt/gfortran and can be called with /opt/gfortran/bin/gfortran You can uninstall this package with sudo gfortran-uninstall
- After installation, in the shell
echo 'export PATH="/opt/gfortran/bin:$PATH"' >> ~/.zshrc source ~/.zshrc # Verify echo $PATH which gfortran gfortran --version R CMD config FC # List any other gfortran on the disk (trouble shooting) sudo find / -type f -name gfortran -perm -111 -print 2>/dev/null | head -n 200 # Install RSpectra export CC=clang export CXX=clang++ export CXX11=clang++ R -e 'install.packages("RSpectra", type="source", INSTALL_opts=c("--no-multiarch","--clean","--verbose"))' R -e 'install.packages("uwot", type="source", INSTALL_opts=c("--no-multiarch","--clean","--verbose"))' - umap_transform() - Add New Points to an Existing Embedding.

- https://cran.r-project.org/web/packages/umap/index.html
- Iris example.
- Note by default umap(, preserve.seed = TRUE). When umap() starts, it saves the current state of the global R RNG (Random Number Generator).
- The global R Random Number Generator (RNG) state changes whenever you call a function that generates a pseudo-random number.
- It is better to use the random_state parameter instead of set.seed(). The default value is NA for random_state.
- The default umap parameters are defined in the variable umap.defaults

- predict.umap()
iris.umap = umap::umap(x_train) perturbed.embedding = predict(iris.umap, x_test) head(perturbed.embedding) # 11 x 2
- Iris example.
- Running UMAP for data visualisation in R (M3C package)
- PCA and UMAP with tidymodels
- UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction
- https://www.biorxiv.org/content/early/2018/04/10/298430
- UMAP clustering in Python
- Dimensionality reduction of #TidyTuesday United Nations voting patterns, Dimensionality reduction for #TidyTuesday Billboard Top 100 songs. The embed package was used.
- Tired: PCA + kmeans, Wired: UMAP + GMM
- Tutorial: guidelines for the computational analysis of single-cell RNA sequencing data Andrews 2020.
- One shortcoming of both t-SNE and UMAP is that they both require a user-defined hyperparameter, and the result can be sensitive to the value chosen. Moreover, the methods are stochastic, and providing a good initialization can significantly improve the results of both algorithms.
- Neither visualization algorithm preserves cell-cell distances, so the resulting embedding should not be used directly by downstream analysis methods such as clustering or pseudotime inference.
- UMAP Dimension Reduction, Main Ideas!!!, UMAP: Mathematical Details (clearly explained!!!)
- How Exactly UMAP Works (open it in an incognito window]
- t-SNE and UMAP Study Guide
- UMAP monkey
- Biologists, stop putting UMAP plots in your papers
- Visualizing French Town Data: UMAP Projection of Location and Population
Why Inference is Problematic
UMAP is for Exploration, not Inference
- UMAP is a non-linear projection that warps the original space to preserve local neighbors. It makes assumptions about the data (that it lies on a low-dimensional manifold) and uses techniques from topological data analysis to find the best arrangement.
- Why Inference is Problematic
UMAP: Exploration vs. Inference Feature Statistical Meaning Implication for UMAP Cluster Size In traditional statistics, a larger cluster implies higher density. Meaningless. UMAP optimizes for 'local connectivity' , and the physical size or density of a cluster in the 2D plot is not proportional to the density in the original high-dimensional space. Distance Between Clusters Distance implies a quantitative measure of dissimilarity. Misleading. While UMAP is better than t-SNE at preserving global structure, the exact distances between clusters (how far apart two groups of points are) are an artifact of the algorithm and should not be used to infer the actual degree of separation in the original data. Coordinates (UMAP1, UMAP2) The axes have a defined, independent physical or statistical meaning (e.g., age, income). Uninterpretable. The UMAP coordinates (`UMAP1`, `UMAP2`, etc.) are arbitrary results of a complex, non-linear mathematical transformation and have no direct statistical meaning tied to the original features.
GECO
GECO: gene expression clustering optimization app for non-linear data visualization of patterns
Visualize the random effects
http://www.quantumforest.com/2012/11/more-sense-of-random-effects/
Calibration
- Search by image: graphical explanation of calibration problem
- Does calibrating classification models improve prediction?
- Calibrating a classification model can improve the reliability and accuracy of the predicted probabilities, but it may not necessarily improve the overall prediction performance of the model in terms of metrics such as accuracy, precision, or recall.
- Calibration is about ensuring that the predicted probabilities from a model match the observed proportions of outcomes in the data. This can be important when the predicted probabilities are used to make decisions or when they are presented to users as a measure of confidence or uncertainty.
- However, calibrating a model does not change its ability to discriminate between positive and negative outcomes. In other words, calibration does not affect how well the model separates the classes, but rather how accurately it estimates the probabilities of class membership.
- In some cases, calibrating a model may improve its overall prediction performance by making the predicted probabilities more accurate. However, this is not always the case, and the impact of calibration on prediction performance may vary depending on the specific needs and goals of the analysis.
- A real-world example of calibration in machine learning is in the field of fraud detection. In this case, it might be desirable to have the model predict probabilities of data belonging to each possible class instead of crude class labels. Gaining access to probabilities is useful for a richer interpretation of the responses, analyzing the model shortcomings, or presenting the uncertainty to the end-users ². A guide to model calibration | Wunderman Thompson Technology.
- Another example where calibration is more important than prediction on new samples is in the field of medical diagnosis. In this case, it is important to have well-calibrated probabilities for the presence of a disease, so that doctors can make informed decisions about treatment. For example, if a diagnostic test predicts an 80% chance that a patient has a certain disease, doctors would expect that 80% of the time when such a prediction is made, the patient actually has the disease. This example does not mean that prediction on new samples is not feasible or not a concern, but rather that having well-calibrated probabilities is crucial for making accurate predictions and informed decisions.
- Calibration: the Achilles heel of predictive analytics Calster 2019
- https://www.itl.nist.gov/div898/handbook/pmd/section1/pmd133.htm Calibration and calibration curve.
- Y=voltage (observed), X=temperature (true/ideal). The calibration curve for a thermocouple is often constructed by comparing thermocouple (observed)output to relatively (true)precise thermometer data.
- when a new temperature is measured with the thermocouple, the voltage is converted to temperature terms by plugging the observed voltage into the regression equation and solving for temperature.
- It is important to note that the thermocouple measurements, made on the secondary measurement scale, are treated as the response variable and the more precise thermometer results, on the primary scale, are treated as the predictor variable because this best satisfies the underlying assumptions (Y=observed, X=true) of the analysis.
- Calibration interval
- In almost all calibration applications the ultimate quantity of interest is the true value of the primary-scale measurement method associated with a measurement made on the secondary scale.
- It seems the x-axis and y-axis have similar ranges in many application.
- An Exercise in the Real World of Design and Analysis, Denby, Landwehr, and Mallows 2001. Inverse regression
- How to determine calibration accuracy/uncertainty of a linear regression?
- Linear Regression and Calibration Curves
- Regression and calibration Shaun Burke
- calibrate package
- investr: An R Package for Inverse Estimation. Paper
- The index of prediction accuracy: an intuitive measure useful for evaluating risk prediction models by Kattan and Gerds 2018. The following code demonstrates Figure 2.
# Odds ratio =1 and calibrated model set.seed(666) x = rnorm(1000) z1 = 1 + 0*x pr1 = 1/(1+exp(-z1)) y1 = rbinom(1000,1,pr1) mean(y1) # .724, marginal prevalence of the outcome dat1 <- data.frame(x=x, y=y1) newdat1 <- data.frame(x=rnorm(1000), y=rbinom(1000, 1, pr1)) # Odds ratio =1 and severely miscalibrated model set.seed(666) x = rnorm(1000) z2 = -2 + 0*x pr2 = 1/(1+exp(-z2)) y2 = rbinom(1000,1,pr2) mean(y2) # .12 dat2 <- data.frame(x=x, y=y2) newdat2 <- data.frame(x=rnorm(1000), y=rbinom(1000, 1, pr2)) library(riskRegression) lrfit1 <- glm(y ~ x, data = dat1, family = 'binomial') IPA(lrfit1, newdata = newdat1) # Variable Brier IPA IPA.gain # 1 Null model 0.1984710 0.000000e+00 -0.003160010 # 2 Full model 0.1990982 -3.160010e-03 0.000000000 # 3 x 0.1984800 -4.534668e-05 -0.003114664 1 - 0.1990982/0.1984710 # [1] -0.003160159 lrfit2 <- glm(y ~ x, family = 'binomial') IPA(lrfit2, newdata = newdat1) # Variable Brier IPA IPA.gain # 1 Null model 0.1984710 0.000000 -1.859333763 # 2 Full model 0.5674948 -1.859334 0.000000000 # 3 x 0.5669200 -1.856437 -0.002896299 1 - 0.5674948/0.1984710 # [1] -1.859334
From the simulated data, we see IPA = -3.16e-3 for a calibrated model and IPA = -1.86 for a severely miscalibrated model.
ROC curve
See ROC.
NRI (Net reclassification improvement)
Maximum likelihood
Difference of partial likelihood, profile likelihood and marginal likelihood
EM Algorithm
- https://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm
- Introduction to EM: Gaussian Mixture Models
Mixture model
mixComp: Estimation of the Order of Mixture Distributions
MLE
Efficiency of an estimator
What does it mean by more “efficient” estimator
Inference
infer package
Generalized Linear Model
- Lectures from a course in Simon Fraser University Statistics.
- Advanced Regression from Patrick Breheny.
- Doing magic and analyzing seasonal time series with GAM (Generalized Additive Model) in R
Link function
Link Functions versus Data Transforms
Extract coefficients, z, p-values
Use coef(summary(glmObject))
> coef(summary(glm.D93))
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.044522e+00 0.1708987 1.781478e+01 5.426767e-71
outcome2 -4.542553e-01 0.2021708 -2.246889e+00 2.464711e-02
outcome3 -2.929871e-01 0.1927423 -1.520097e+00 1.284865e-01
treatment2 1.337909e-15 0.2000000 6.689547e-15 1.000000e+00
treatment3 1.421085e-15 0.2000000 7.105427e-15 1.000000e+00
Quasi Likelihood
Quasi-likelihood is like log-likelihood. The quasi-score function (first derivative of quasi-likelihood function) is the estimating equation.
- Original paper by Peter McCullagh.
- Lecture 20 from SFU.
- U. Washington and another lecture focuses on overdispersion.
- This lecture contains a table of quasi likelihood from common distributions.
IRLS
- glmnet v4.0: generalizing the family parameter
- Generalized linear models, abridged (include algorithm and code)
Plot
Deviance, stats::deviance() and glmnet::deviance.glmnet() from R
- It is a generalization of the idea of using the sum of squares of residuals (RSS) in ordinary least squares to cases where model-fitting is achieved by maximum likelihood. See What is Deviance? (specifically in CART/rpart) to manually compute deviance and compare it with the returned value of the deviance() function from a linear regression. Summary: deviance() = RSS in linear models.
- Interpreting Generalized Linear Models
- What is deviance? You can think of the deviance of a model as twice the negative log likelihood plus a constant.
- https://www.rdocumentation.org/packages/stats/versions/3.4.3/topics/deviance
- Likelihood ratio tests and the deviance http://data.princeton.edu/wws509/notes/a2.pdf#page=6
- Deviance(y,muhat) = 2*(loglik_saturated - loglik_proposed)
- Binomial GLM and the objects() function that seems to be the same as str(, max=1).
- Interpreting Residual and Null Deviance in GLM R
- Null Deviance = 2(LL(Saturated Model) - LL(Null Model)) on df = df_Sat - df_Null. The null deviance shows how well the response variable is predicted by a model that includes only the intercept (grand mean).
- Residual Deviance = 2(LL(Saturated Model) - LL(Proposed Model)) = [math]\displaystyle{ 2(LL(y|y) - LL(\hat{\mu}|y)) }[/math], df = df_Sat - df_Proposed=n-p. ==> deviance() has returned.
- Null deviance > Residual deviance. Null deviance df = n-1. Residual deviance df = n-p.
## an example with offsets from Venables & Ripley (2002, p.189)
utils::data(anorexia, package = "MASS")
anorex.1 <- glm(Postwt ~ Prewt + Treat + offset(Prewt),
family = gaussian, data = anorexia)
summary(anorex.1)
# Call:
# glm(formula = Postwt ~ Prewt + Treat + offset(Prewt), family = gaussian,
# data = anorexia)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -14.1083 -4.2773 -0.5484 5.4838 15.2922
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 49.7711 13.3910 3.717 0.000410 ***
# Prewt -0.5655 0.1612 -3.509 0.000803 ***
# TreatCont -4.0971 1.8935 -2.164 0.033999 *
# TreatFT 4.5631 2.1333 2.139 0.036035 *
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# (Dispersion parameter for gaussian family taken to be 48.69504)
#
# Null deviance: 4525.4 on 71 degrees of freedom
# Residual deviance: 3311.3 on 68 degrees of freedom
# AIC: 489.97
#
# Number of Fisher Scoring iterations: 2
deviance(anorex.1)
# [1] 3311.263
- In glmnet package. The deviance is defined to be 2*(loglike_sat - loglike), where loglike_sat is the log-likelihood for the saturated model (a model with a free parameter per observation). Null deviance is defined to be 2*(loglike_sat -loglike(Null)); The NULL model refers to the intercept model, except for the Cox, where it is the 0 model. Hence dev.ratio=1-deviance/nulldev, and this deviance method returns (1-dev.ratio)*nulldev.
x=matrix(rnorm(100*2),100,2) y=rnorm(100) fit1=glmnet(x,y) deviance(fit1) # one for each lambda # [1] 98.83277 98.53893 98.29499 98.09246 97.92432 97.78472 97.66883 # [8] 97.57261 97.49273 97.41327 97.29855 97.20332 97.12425 97.05861 # ... # [57] 96.73772 96.73770 fit2 <- glmnet(x, y, lambda=.1) # fix lambda deviance(fit2) # [1] 98.10212 deviance(glm(y ~ x)) # [1] 96.73762 sum(residuals(glm(y ~ x))^2) # [1] 96.73762
Saturated model
- The saturated model always has n parameters where n is the sample size.
- Logistic Regression : How to obtain a saturated model
Testing
- Robust testing in generalized linear models by sign flipping score contributions
- Goodness‐of‐fit testing in high dimensional generalized linear models
Generalized Additive Models
- How to solve common problems with GAMs
- Generalized Additive Models: Allowing for some wiggle room in your models
- Simulating data from a non-linear function by specifying a handful of points
- Modeling the secular trend in a cluster randomized trial using very flexible models
Penalty
From Math to Code: Building GAM with Penalty Functions From Scratch
Simulate data
- Fake Data with R
- Understanding statistics through programming: You don’t really understand a stochastic process until you know how to simulate it - D.G. Kendall.
Density plot
# plot a Weibull distribution with shape and scale func <- function(x) dweibull(x, shape = 1, scale = 3.38) curve(func, .1, 10) func <- function(x) dweibull(x, shape = 1.1, scale = 3.38) curve(func, .1, 10)
The shape parameter plays a role on the shape of the density function and the failure rate.
- Shape <=1: density is convex, not a hat shape.
- Shape =1: failure rate (hazard function) is constant. Exponential distribution.
- Shape >1: failure rate increases with time
Simulate data from a specified density
Permuted block randomization
Permuted block randomization using simstudy
- How To Generate Correlated Data In R
- Flexible correlation generation: an update to genCorMat in simstudy
- Cholesky decomposition
set.seed(1) n <- 1000 R <- matrix(c(1, 0.75, 0.75, 1), nrow=2) M <- matrix(rnorm(2 * n), ncol=2) M <- M %*% chol(R) # chol(R) is an upper triangular matrix x <- M[, 1] # First correlated vector y <- M[, 2] cor(x, y) # 0.7502607
- GenOrd: Generate ordinal and discrete variables with given correlation matrix and marginal distributions, here
Clustered data with marginal correlations
Generating clustered data with marginal correlations
Signal to noise ratio/SNR
- https://en.wikipedia.org/wiki/Signal-to-noise_ratio
- https://stats.stackexchange.com/questions/31158/how-to-simulate-signal-noise-ratio
- [math]\displaystyle{ SNR = \frac{\sigma^2_{signal}}{\sigma^2_{noise}} = \frac{Var(f(X))}{Var(e)} }[/math] if Y = f(X) + e
- The SNR is related to the correlation of Y and f(X). Assume X and e are independent ([math]\displaystyle{ X \perp e }[/math]):
- [math]\displaystyle{
\begin{align}
Cor(Y, f(X)) &= Cor(f(X)+e, f(X)) \\
&= \frac{Cov(f(X)+e, f(X))}{\sqrt{Var(f(X)+e) Var(f(X))}} \\
&= \frac{Var(f(X))}{\sqrt{Var(f(X)+e) Var(f(X))}} \\
&= \frac{\sqrt{Var(f(X))}}{\sqrt{Var(f(X)) + Var(e))}} = \frac{\sqrt{SNR}}{\sqrt{SNR + 1}} \\
&= \frac{1}{\sqrt{1 + Var(e)/Var(f(X))}} = \frac{1}{\sqrt{1 + SNR^{-1}}}
\end{align}
}[/math]
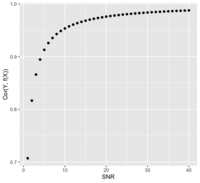
- Or [math]\displaystyle{ SNR = \frac{Cor^2}{1-Cor^2} }[/math]
- Page 401 of ESLII (https://web.stanford.edu/~hastie/ElemStatLearn//) 12th print.
Some examples of signal to noise ratio
- ESLII_print12.pdf: .64, 5, 4
- Yuan and Lin 2006: 1.8, 3
- A framework for estimating and testing qualitative interactions with applications to predictive biomarkers Roth, Biostatistics, 2018
- Matlab: computing signal to noise ratio (SNR) of two highly correlated time domain signals
Effect size, Cohen's d and volcano plot
- https://en.wikipedia.org/wiki/Effect_size (See also the estimation by the pooled sd)
- [math]\displaystyle{ \theta = \frac{\mu_1 - \mu_2} \sigma, }[/math]
- Effect size, sample size and power from ebook Learning statistics with R: A tutorial for psychology students and other beginners.
- t-statistic and Cohen's d for the case of mean difference between two independent groups
- Cohen’s D for Experimental Planning
- Common Effect Size Measures:
Common Effect Size Measures Type of Analysis Effect Size Measure Interpretation Mean Comparison (t-test, ANOVA) Cohen’s d Difference in standard deviation units Regression Standardized β (beta) Strength of predictor variables Correlation Pearson’s r Strength & direction of relationship (-1 to 1) Categorical Data (Chi-square, Logistic Regression) Odds Ratio (OR), Risk Ratio (RR) Strength of association - Volcano plot
- Y-axis: -log(p)
- X-axis: log2 fold change OR effect size (Cohen's D). An example from RNA-Seq data.
- Compute Fisher’s Exact Test Power in R.
- The Exact package. power.exact.test() function.
Treatment/control
- simdata() from biospear package
- data.gen() from ROCSI package. The response contains continuous, binary and survival outcomes. The input include prevalence of predictive biomarkers, effect size (beta) for prognostic biomarker, etc.
Cauchy distribution has no expectation
https://en.wikipedia.org/wiki/Cauchy_distribution
replicate(10, mean(rcauchy(10000)))
Dirichlet distribution
- Dirichlet distribution
- It is a multivariate generalization of the beta distribution
- The Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution.
- dirmult::rdirichlet()
Relationships among probability distributions
https://en.wikipedia.org/wiki/Relationships_among_probability_distributions
What is the probability that two persons have the same initials
The post. The probability that at least two persons have the same initials depends on the size of the group. For a team of 8 people, simulations suggest that the probability is close to 4.1%. This probability increases with the size of the group. If there are 1000 people in the room, the probability is almost 100%. How many people do you need to guarantee that two of them have the same initals?
Multiple comparisons
- If you perform experiments over and over, you's bound to find something. So significance level must be adjusted down when performing multiple hypothesis tests.
- http://www.gs.washington.edu/academics/courses/akey/56008/lecture/lecture10.pdf
- Book 'Multiple Comparison Using R' by Bretz, Hothorn and Westfall, 2011.
- Plot a histogram of p-values, a post from varianceexplained.org. The anti-conservative histogram (tail on the RHS) is what we have typically seen in e.g. microarray gene expression data.
- Comparison of different ways of multiple-comparison in R.
- Comparing multiple comparisons: practical guidance for choosing the best multiple comparisons test Midway 2020
Take an example, Suppose 550 out of 10,000 genes are significant at .05 level
- P-value < .05 ==> Expect .05*10,000=500 false positives
- False discovery rate < .05 ==> Expect .05*550 =27.5 false positives
- Family wise error rate < .05 ==> The probablity of at least 1 false positive <.05
According to Lifetime Risk of Developing or Dying From Cancer, there is a 39.7% risk of developing a cancer for male during his lifetime (in other words, 1 out of every 2.52 men in US will develop some kind of cancer during his lifetime) and 37.6% for female. So the probability of getting at least one cancer patient in a 3-generation family is 1-.6**3 - .63**3 = 0.95.
Flexible method
?GSEABenchmarkeR::runDE. Unadjusted (too few DE genes), FDR, and Bonferroni (too many DE genes) are applied depending on the proportion of DE genes.
Family-Wise Error Rate (FWER)
- https://en.wikipedia.org/wiki/Family-wise_error_rate
- How to Estimate the Family-wise Error Rate
- Multiple Hypothesis Testing in R
Bonferroni
- https://en.wikipedia.org/wiki/Bonferroni_correction
- This correction method is the most conservative of all and due to its strict filtering, potentially increases the false negative rate which simply means rejecting true positives among false positives.
False Discovery Rate/FDR
- https://en.wikipedia.org/wiki/False_discovery_rate
- Paper Definition by Benjamini and Hochberg in JRSS B 1995.
- False Discovery Rates, FDR, clearly explained by StatQuest
- A comic
- A p-value of 0.05 implies that 5% of all tests will result in false positives. An FDR adjusted p-value (or q-value) of 0.05 implies that 5% of significant tests will result in false positives. The latter will result in fewer false positives.
- How to interpret False Discovery Rate?
- P-value vs false discovery rate vs family wise error rate. See 10 statistics tip or Statistics for Genomics (140.688) from Jeff Leek. Suppose 550 out of 10,000 genes are significant at .05 level
- P-value < .05 implies expecting .05*10000 = 500 false positives (if we consider 50 hallmark genesets, 50*.05=2.5)
- False discovery rate < .05 implies expecting .05*550 = 27.5 false positives
- Family wise error rate (P (# of false positives ≥ 1)) < .05. See Understanding Family-Wise Error Rate
- Statistical significance for genomewide studies by Storey and Tibshirani.
- What’s the probability that a significant p-value indicates a true effect?
- http://onetipperday.sterding.com/2015/12/my-note-on-multiple-testing.html
- A practical guide to methods controlling false discoveries in computational biology by Korthauer, et al 2018, BMC Genome Biology 2019
- onlineFDR: an R package to control the false discovery rate for growing data repositories
- An estimate of the science-wise false discovery rate and application to the top medical literature Jager & Leek 2021
- The adjusted p-value (also known as the False Discovery Rate or FDR) and the raw p-value can be close under certain conditions. study on multiple outcomes- do I adjust or not adjust p-values?
- The number of tests is small: When performing multiple hypothesis tests, the adjustment for multiple comparisons (like Bonferroni or Benjamini-Hochberg procedures) can have a smaller impact if the number of tests is small. This is because these adjustments are less stringent when fewer tests are conducted.
- The p-values are very small: If the raw p-values are very small to begin with, then even after adjustment, they may still remain small. This is especially true for methods that control the FDR, like the Benjamini-Hochberg procedure, which tend to be less conservative than methods controlling the Family-Wise Error Rate (FWER), like the Bonferroni correction.
- The tests are not independent: Some p-value adjustment methods assume that the tests are independent. If this assumption is violated, the adjusted p-values may not be accurate.
- The Benjamini-Hochberg Procedure (FDR) And P-Value Adjusted Explained
Suppose [math]\displaystyle{ p_1 \leq p_2 \leq ... \leq p_n }[/math]. Then
- [math]\displaystyle{ \text{FDR}_i = \text{min}(1, n* p_i/i) }[/math].
- If the number of tests ([math]\displaystyle{ n }[/math]) is large and/or the original p value ([math]\displaystyle{ p_i }[/math]) is large, then FDR can hit the value 1.
- For large n,
- For early ranks (small 𝑖), the multiplier [math]\displaystyle{ n/i }[/math] is large. But if you’re at the top of the list with a very small raw p-value, the adjusted value can still stay small, because the raw p is tiny enough to survive the scaling.
- For middle/late ranks (larger i), the factor [math]\displaystyle{ n/i }[/math] is smaller (closer to 1), so adjusted p-values are closer to the raw p.
- Monotonic adjustment
- The simple formula above does not guarantee the monotonicity property from the FDR. So the calculation in R is more complicated. See How Does R Calculate the False Discovery Rate.
- Example: if pval=c(0.01,0.02,0.021,0.04,0.05), then p.adjust(pval, "BH") = c(.035, .035, .035, .050, .050) instead c(.05, .05, .035, .05, .05) if we only apply the formula n*p/i. So the adjusted p is applying the backward cumulative minimum to enforce monotonicity.
- n/i*pi = c(.05, .05, .035, .05, .05)
- Apply the backward cumulative minimum. i=5 -> .05. i=4 -> min(.05, .05)=.05, i=3 -> min(.035, .05)=.035, i=2 -> min(.05, .035)=.035. i=1 -> min(0.05, .035) = .035.
- To ensure interpretability, the standard BH implementation applies a correction step. This makes the adjusted p-values non-decreasing with rank [math]\displaystyle{ i }[/math].
- [math]\displaystyle{ p_{(i)}^{BH} = \min_{j \geq i} (\frac{n}{j} * p_{(j)}) }[/math]
- Below is the histograms of p-values and FDR (BH adjusted) from a real data (Pomeroy in BRB-ArrayTools). File:Hist bh.svg
- And the next is a scatterplot w/ histograms on the margins from a null data. The curve looks like f(x)=log(x). File:Scatterhist.svg
q-value
- https://en.wikipedia.org/wiki/Q-value_(statistics)
- Understanding p value, multiple comparisons, FDR and q value
q-value is defined as the minimum FDR that can be attained when calling that feature significant (i.e., expected proportion of false positives incurred when calling that feature significant).
If gene X has a q-value of 0.013 it means that 1.3% of genes that show p-values at least as small as gene X are false positives.
Another view: q-value = FDR adjusted p-value. A p-value of 5% means that 5% of all tests will result in false positives. A q-value of 5% means that 5% of significant results will result in false positives. here.
Double dipping
SAM/Significance Analysis of Microarrays
The percentile option is used to define the number of falsely called genes based on 'B' permutations. If we use the 90-th percentile, the number of significant genes will be less than if we use the 50-th percentile/median.
In BRCA dataset, using the 90-th percentile will get 29 genes vs 183 genes if we use median.
Required number of permutations for a permutation-based p-value
- Permutation tests
- https://stats.stackexchange.com/a/80879
- Multinomial coefficient. multichoose()
library("iterpc")
multichoose(c(3,1,1)) # [1] 20
multichoose(c(10,10)) |> log10() # [1] 5.266599
multichoose(c(100,100), bigz = T) |> log10() # [1] 58.95688
multichoose(c(100,100,100), bigz = T) |> log10() # [1] 140.5758
Multivariate permutation test
In BRCA dataset, using 80% confidence gives 116 genes vs 237 genes if we use 50% confidence (assuming maximum proportion of false discoveries is 10%). The method is published on EL Korn, JF Troendle, LM McShane and R Simon, Controlling the number of false discoveries: Application to high dimensional genomic data, Journal of Statistical Planning and Inference, vol 124, 379-398 (2004).
The role of the p-value in the multitesting problem
https://www.tandfonline.com/doi/full/10.1080/02664763.2019.1682128
String Permutations Algorithm
combinat package
coin package: Resampling
Solving the Empirical Bayes Normal Means Problem with Correlated Noise Sun 2018
The package cashr and the source code of the paper
Bayes
Bayes factor
Empirical Bayes method
- http://en.wikipedia.org/wiki/Empirical_Bayes_method
- Introduction to Empirical Bayes: Examples from Baseball Statistics
Naive Bayes classifier
Understanding Naïve Bayes Classifier Using R
MCMC
Speeding up Metropolis-Hastings with Rcpp
offset() function
- An offset is a term to be added to a linear predictor, such as in a generalised linear model, with known coefficient 1 rather than an estimated coefficient.
- https://www.rdocumentation.org/packages/stats/versions/3.5.0/topics/offset
Offset in Poisson regression
- http://rfunction.com/archives/223
- https://stats.stackexchange.com/questions/11182/when-to-use-an-offset-in-a-poisson-regression
- We need to model rates instead of counts
- More generally, you use offsets because the units of observation are different in some dimension (different populations, different geographic sizes) and the outcome is proportional to that dimension.
An example from here
Y <- c(15, 7, 36, 4, 16, 12, 41, 15) N <- c(4949, 3534, 12210, 344, 6178, 4883, 11256, 7125) x1 <- c(-0.1, 0, 0.2, 0, 1, 1.1, 1.1, 1) x2 <- c(2.2, 1.5, 4.5, 7.2, 4.5, 3.2, 9.1, 5.2) glm(Y ~ offset(log(N)) + (x1 + x2), family=poisson) # two variables # Coefficients: # (Intercept) x1 x2 # -6.172 -0.380 0.109 # # Degrees of Freedom: 7 Total (i.e. Null); 5 Residual # Null Deviance: 10.56 # Residual Deviance: 4.559 AIC: 46.69 glm(Y ~ offset(log(N)) + I(x1+x2), family=poisson) # one variable # Coefficients: # (Intercept) I(x1 + x2) # -6.12652 0.04746 # # Degrees of Freedom: 7 Total (i.e. Null); 6 Residual # Null Deviance: 10.56 # Residual Deviance: 8.001 AIC: 48.13
Offset in Cox regression
An example from biospear::PCAlasso()
coxph(Surv(time, status) ~ offset(off.All), data = data) # Call: coxph(formula = Surv(time, status) ~ offset(off.All), data = data) # # Null model # log likelihood= -2391.736 # n= 500 # versus without using offset() coxph(Surv(time, status) ~ off.All, data = data) # Call: # coxph(formula = Surv(time, status) ~ off.All, data = data) # # coef exp(coef) se(coef) z p # off.All 0.485 1.624 0.658 0.74 0.46 # # Likelihood ratio test=0.54 on 1 df, p=0.5 # n= 500, number of events= 438 coxph(Surv(time, status) ~ off.All, data = data)$loglik # [1] -2391.702 -2391.430 # initial coef estimate, final coef
Offset in linear regression
- https://www.rdocumentation.org/packages/stats/versions/3.5.1/topics/lm
- https://stackoverflow.com/questions/16920628/use-of-offset-in-lm-regression-r
Overdispersion
https://en.wikipedia.org/wiki/Overdispersion
Var(Y) = phi * E(Y). If phi > 1, then it is overdispersion relative to Poisson. If phi <1, we have under-dispersion (rare).
Heterogeneity
The Poisson model fit is not good; residual deviance/df >> 1. The lack of fit maybe due to missing data, covariates or overdispersion.
Subjects within each covariate combination still differ greatly.
- https://onlinecourses.science.psu.edu/stat504/node/169.
- https://onlinecourses.science.psu.edu/stat504/node/162
Consider Quasi-Poisson or negative binomial.
Test of overdispersion or underdispersion in Poisson models
Poisson
- https://en.wikipedia.org/wiki/Poisson_distribution
- The “Poisson” Distribution: History, Reenactments, Adaptations
- The Poisson distribution: From basic probability theory to regression models
- Tutorial: Poisson Regression in R
- We can use a quasipoisson model, which allows the variance to be proportional rather than equal to the mean. glm(, family="quasipoisson", ).
- Generalized Linear Models in R from sscc.wisc.
- See the R code in the supplement of the paper Interrupted time series regression for the evaluation of public health interventions: a tutorial 2016
Negative Binomial
The mean of the Poisson distribution can itself be thought of as a random variable drawn from the gamma distribution thereby introducing an additional free parameter.
Binomial
- Generating and modeling over-dispersed binomial data
- Simulate! Simulate! - Part 4: A binomial generalized linear mixed model
- simstudy package. The final data sets can represent data from randomized control trials, repeated measure (longitudinal) designs, and cluster randomized trials. Missingness can be generated using various mechanisms (MCAR, MAR, NMAR). Analyzing a binary outcome arising out of within-cluster, pair-matched randomization. Generating probabilities for ordinal categorical data.
- Binomial Confidence Intervals for Rare Events: Importance of Defining Margin of Error Relative to Magnitude of Proportion. Wald, Clopper-Pearson (exact), Wilson and Agresti-Coull.
Count data
Zero counts
Bias
Bias in Small-Sample Inference With Count-Data Models Blackburn 2019
Survival data analysis
Logistic regression
Simulate binary data from the logistic model
set.seed(666) x1 = rnorm(1000) # some continuous variables x2 = rnorm(1000) z = 1 + 2*x1 + 3*x2 # linear combination with a bias pr = 1/(1+exp(-z)) # pass through an inv-logit function y = rbinom(1000,1,pr) # bernoulli response variable #now feed it to glm: df = data.frame(y=y,x1=x1,x2=x2) glm( y~x1+x2,data=df,family="binomial")
Building a Logistic Regression model from scratch
https://www.analyticsvidhya.com/blog/2015/10/basics-logistic-regression
Algorithm didn’t converge & probabilities 0/1
- glm.fit Warning Messages in R: algorithm didn’t converge & probabilities 0/1
- Why am I getting "algorithm did not converge" and "fitted prob numerically 0 or 1" warnings with glm?
Prediction
- Confused with the reference level in logistic regression in R
- Binary Logistic Regression With R. The prediction values returned from predict(fit, type = "response") are the probability that a new observation is from class 1 (instead of class 0); the second level. We can convert this probability into a class label by using ifelse(pred > 0.5, 1, 0).
- GLM in R: Generalized Linear Model with Example
- Logistic Regression – A Complete Tutorial With Examples in R. caret's downSample()/upSample() was used.
library(caret) table(oilType) # oilType # A B C D E F G # 37 26 3 7 11 10 2 dim(fattyAcids) # [1] 96 7 dim(upSample(fattyAcids, oilType)) # [1] 259 8 table(upSample(fattyAcids, oilType)$Class) # A B C D E F G # 37 37 37 37 37 37 37 table(downSample(fattyAcids, oilType)$Class) # A B C D E F G # 2 2 2 2 2 2 2
- Downsampling for predictive modeling
Odds ratio
- https://en.wikipedia.org/wiki/Odds_ratio.
- Odds ratio was used in the case of 2x2 contingency table.
- Odds ratio can be applied to the logistic regression.
- It seems a larger OR does not imply a smaller Fisher's exact p-value. See an example on Fig 4 here.
- Odds ratio = exp(coefficient). For example, if the coefficient for a predictor variable in your logistic regression model is 0.5, the odds ratio for that variable would be: exp(0.5) = 1.64. This means that, for every unit increase in the predictor variable, the odds of the binary outcome occurring increase by a factor of 1.64. A larger odds ratio indicates a stronger association between the predictor variable and the binary outcome, while a smaller odds ratio indicates a weaker association.
- Why the odds ratio is exp(coefficient) in logistic regression? The odds ratio is the exponent of the coefficient in a logistic regression model because the logistic regression model is based on the logit function, which is the natural logarithm of the odds ratio. The logit function takes the following form: logit(p) = log(p/(1-p)), where p is the probability of the binary outcome occurring.
- Clinical example: Imagine that you are conducting a study to investigate the association between body mass index (BMI) and the risk of developing type 2 diabetes. Fit a logistic regression using BMI as the covariate. Calculate the odds ratio for the BMI variable: exp(coefficient) = 1.64. This means that, for every unit increase in BMI, the odds of a patient developing type 2 diabetes increase by a factor of 1.64.
- Probability vs. odds: Probability and odds can differ from each other in many ways. For example, probability (of an event) typically appears as a percentage, while you can express odds as a fraction or ratio (the ratio of the number of ways the event can occur to the number of ways it cannot occur). Another difference is that probability uses a range that only exists between the numbers zero and one, while odds use a range that has no limits.
- Calculate the odds ratio from the coefficient estimates; see this post.
require(MASS) N <- 100 # generate some data X1 <- rnorm(N, 175, 7) X2 <- rnorm(N, 30, 8) X3 <- abs(rnorm(N, 60, 30)) Y <- 0.5*X1 - 0.3*X2 - 0.4*X3 + 10 + rnorm(N, 0, 12) # dichotomize Y and do logistic regression Yfac <- cut(Y, breaks=c(-Inf, median(Y), Inf), labels=c("lo", "hi")) glmFit <- glm(Yfac ~ X1 + X2 + X3, family=binomial(link="logit")) exp(cbind(coef(glmFit), confint(glmFit)))
AUC
A small introduction to the ROCR package
predict.glm() ROCR::prediction() ROCR::performance() glmobj ------------> predictTest -----------------> ROCPPred ---------> AUC newdata labels
Gompertz function
Medical applications
RCT
- The design effect of a cluster randomized trial with baseline measurements
- Explaining a Causal Forest
- An Example to Illustrate Randomized Trial Estimands and Estimators
- Planning for a 3-arm cluster randomized trial with a nested intervention and a time-to-event outcome
Subgroup analysis
Other related keywords: recursive partitioning, randomized clinical trials (RCT)
- Thinking about different ways to analyze sub-groups in an RCT
- Tutorial in biostatistics: data-driven subgroup identification and analysis in clinical trials I Lipkovich, A Dmitrienko - Statistics in medicine, 2017
- Personalized medicine:Four perspectives of tailored medicine SJ Ruberg, L Shen - Statistics in Biopharmaceutical Research, 2015
- Berger, J. O., Wang, X., and Shen, L. (2014), “A Bayesian Approach to Subgroup Identification,” Journal of Biopharmaceutical Statistics, 24, 110–129.
- Change over time is not "treatment response"
- Inference on Selected Subgroups in Clinical Trials Guo 2020
- BioPred - An R Package for Biomarkers Analysis in Precision Medicine. Bioinformatics 2024
Interaction analysis
- Goal: assessing the predictiveness of biomarkers by testing their interaction (strength) with the treatment.
- Prognostics vs predictive marker including quantitative and qualitative interactions.
- Evaluation of biomarkers for treatment selection usingindividual participant data from multiple clinical trials Kang et al 2018
- http://www.stat.purdue.edu/~ghobbs/STAT_512/Lecture_Notes/ANOVA/Topic_27.pdf#page=15. For survival data, y-axis is the survival time and B1=treatment, B2=control and X-axis is treatment-effect modifying score. But as seen on page16, the effects may not be separated.
- Identification of biomarker-by-treatment interactions in randomized clinical trials with survival outcomes and high-dimensional spaces N Ternès, F Rotolo, G Heinze, S Michiels - Biometrical Journal, 2017
- Designing a study to evaluate the benefitof a biomarker for selectingpatient treatment Janes 2015
- A visualization method measuring theperformance of biomarkers for guidingtreatment decisions Yang et al 2015. Predictiveness curves were used a lot.
- Combining Biomarkers to Optimize Patient TreatmentRecommendations Kang et al 2014. Several simulations are conducted.
- An approach to evaluating and comparing biomarkers for patient treatment selection Janes et al 2014
- A Framework for Evaluating Markers Used to Select Patient Treatment Janes et al 2014
- Tian, L., Alizaden, A. A., Gentles, A. J., and Tibshirani, R. (2014) “A Simple Method for Detecting Interactions Between a Treatment and a Large Number of Covariates,” and the book chapter.
- Statistical Methods for Evaluating and Comparing Biomarkers for Patient Treatment Selection Janes et al 2013
- Assessing Treatment-Selection Markers using a Potential Outcomes Framework Huang et al 2012
- Methods for Evaluating Prediction Performance of Biomarkers and Tests Pepe et al 2012
- Measuring the performance of markers for guiding treatment decisions by Janes, et al 2011.
cf <- c(2, 1, .5, 0) f1 <- function(x) { z <- cf[1] + cf[3] + (cf[2]+cf[4])*x; 1/ (1 + exp(-z)) } f0 <- function(x) { z <- cf[1] + cf[2]*x; 1/ (1 + exp(-z)) } par(mfrow=c(1,3)) curve(f1, -3, 3, col = 'red', ylim = c(0, 1), ylab = '5-year DFS Rate', xlab = 'Marker A/D Value', main = 'Predictiveness Curve', lwd = 2) curve(f0, -3, 3, col = 'black', ylim = c(0, 1), xlab = '', ylab = '', lwd = 2, add = TRUE) legend(.5, .4, c("control", "treatment"), col = c("black", "red"), lwd = 2) cf <- c(.1, 1, -.1, .5) curve(f1, -3, 3, col = 'red', ylim = c(0, 1), ylab = '5-year DFS Rate', xlab = 'Marker G Value', main = 'Predictiveness Curve', lwd = 2) curve(f0, -3, 3, col = 'black', ylim = c(0, 1), xlab = '', ylab = '', lwd = 2, add = TRUE) legend(.5, .4, c("control", "treatment"), col = c("black", "red"), lwd = 2) abline(v= - cf[3]/cf[4], lty = 2) cf <- c(1, -1, 1, 2) curve(f1, -3, 3, col = 'red', ylim = c(0, 1), ylab = '5-year DFS Rate', xlab = 'Marker B Value', main = 'Predictiveness Curve', lwd = 2) curve(f0, -3, 3, col = 'black', ylim = c(0, 1), xlab = '', ylab = '', lwd = 2, add = TRUE) legend(.5, .85, c("control", "treatment"), col = c("black", "red"), lwd = 2) abline(v= - cf[3]/cf[4], lty = 2)File:PredcurveLogit.svg - An Approach to Evaluating and Comparing Biomarkers for Patient Treatment Selection The International Journal of Biostatistics by Janes, 2014. Y-axis is risk given marker, not P(T > t0|X). Good details.
- Gunter, L., Zhu, J., and Murphy, S. (2011), “Variable Selection for Qualitative Interactions in Personalized Medicine While Controlling the Family-Wise Error Rate,” Journal of Biopharmaceutical Statistics, 21, 1063–1078.
Statistical Learning
- Elements of Statistical Learning Book homepage
- An Introduction to Statistical Learning with Applications in R/ISLR], pdf
- A Computational Approach to Statistical Learning by Taylor Arnold, Michael Kane, and Bryan Lewis. Chap 8 Neural Networks.
- From Linear Models to Machine Learning by Norman Matloff
- 10 Free Must-Read Books for Machine Learning and Data Science
- 10 Statistical Techniques Data Scientists Need to Master
- Linear regression
- Classification: Logistic Regression, Linear Discriminant Analysis, Quadratic Discriminant Analysis
- Resampling methods: Bootstrapping and Cross-Validation
- Subset selection: Best-Subset Selection, Forward Stepwise Selection, Backward Stepwise Selection, Hybrid Methods
- Shrinkage/regularization: Ridge regression, Lasso
- Dimension reduction: Principal Components Regression, Partial least squares
- Nonlinear models: Piecewise function, Spline, generalized additive model
- Tree-based methods: Bagging, Boosting, Random Forest
- Support vector machine
- Unsupervised learning: PCA, k-means, Hierarchical
- 15 Types of Regression you should know
- Is a Classification Procedure Good Enough?—A Goodness-of-Fit Assessment Tool for Classification Learning Zhang 2021 JASA
LDA (Fisher's linear discriminant), QDA
- https://en.wikipedia.org/wiki/Linear_discriminant_analysis.
- Assumptions: Multivariate normality, Homogeneity of variance/covariance, Multicollinearity, Independence.
- The common variance is calculated by the pooled covariance matrix just like the t-test case.
- Logistic regression has none-the-less become the common choice, since the assumptions of discriminant analysis are rarely met.
- How to perform Logistic Regression, LDA, & QDA in R
- Discriminant Analysis: Statistics All The Way
- Multiclass linear discriminant analysis with ultrahigh‐dimensional features Li 2019
- Linear Discriminant Analysis – Bit by Bit
Bagging
Chapter 8 of the book.
- Bootstrap mean is approximately a posterior average.
- Bootstrap aggregation or bagging average: Average the prediction over a collection of bootstrap samples, thereby reducing its variance. The bagging estimate is defined by
- [math]\displaystyle{ \hat{f}_{bag}(x) = \frac{1}{B}\sum_{b=1}^B \hat{f}^{*b}(x). }[/math]
Where Bagging Might Work Better Than Boosting
CLASSIFICATION FROM SCRATCH, BAGGING AND FORESTS 10/8
Boosting
- Ch8.2 Bagging, Random Forests and Boosting of An Introduction to Statistical Learning and the code.
- An Attempt To Understand Boosting Algorithm
- gbm package. An implementation of extensions to Freund and Schapire's AdaBoost algorithm and Friedman's gradient boosting machine. Includes regression methods for least squares, absolute loss, t-distribution loss, quantile regression, logistic, multinomial logistic, Poisson, Cox proportional hazards partial likelihood, AdaBoost exponential loss, Huberized hinge loss, and Learning to Rank measures (LambdaMart).
- https://www.biostat.wisc.edu/~kendzior/STAT877/illustration.pdf
- http://www.is.uni-freiburg.de/ressourcen/business-analytics/10_ensemblelearning.pdf and exercise
- Classification from scratch
- Boosting in Machine Learning:-A Brief Overview
AdaBoost
AdaBoost.M1 by Freund and Schapire (1997):
The error rate on the training sample is [math]\displaystyle{ \bar{err} = \frac{1}{N} \sum_{i=1}^N I(y_i \neq G(x_i)), }[/math]
Sequentially apply the weak classification algorithm to repeatedly modified versions of the data, thereby producing a sequence of weak classifiers [math]\displaystyle{ G_m(x), m=1,2,\dots,M. }[/math]
The predictions from all of them are combined through a weighted majority vote to produce the final prediction: [math]\displaystyle{ G(x) = sign[\sum_{m=1}^M \alpha_m G_m(x)]. }[/math] Here [math]\displaystyle{ \alpha_1,\alpha_2,\dots,\alpha_M }[/math] are computed by the boosting algorithm and weight the contribution of each respective [math]\displaystyle{ G_m(x) }[/math]. Their effect is to give higher influence to the more accurate classifiers in the sequence.
Dropout regularization
DART: Dropout Regularization in Boosting Ensembles
Gradient boosting
- https://en.wikipedia.org/wiki/Gradient_boosting
- Machine Learning Basics - Gradient Boosting & XGBoost
- Gradient Boosting Essentials in R Using XGBOOST
- Is catboost the best gradient boosting R package?
Gradient descent
Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function.
- Gradient Descent, Step-by-Step (video) StatQuest. Step size and learning rate.
- Gradient descent is very useful when it is not possible to solve for where the derivative = 0
- New parameter = Old parameter - Step size where Step size = slope(or gradient) * Learning rate.
- Stochastic Gradient Descent, Clearly Explained!!!
- An Introduction to Gradient Descent and Linear Regression Easy to understand based on simple linear regression. Python code is provided too. The unknown parameter is the learning rate.
- Gradient Descent in R by Econometric Sense. Example of using the trivial cost function 1.2 * (x-2)^2 + 3.2. R code is provided and visualization of steps is interesting! The unknown parameter is the learning rate.
repeat until convergence { Xn+1 = Xn - α∇F(Xn) }Where ∇F(x) would be the derivative for the cost function at hand and α is the learning rate.
- Regression via Gradient Descent in R by Econometric Sense.
- Applying gradient descent – primer / refresher
- An overview of Gradient descent optimization algorithms
- A Complete Tutorial on Ridge and Lasso Regression in Python
- How to choose the learning rate?
- Machine learning from Andrew Ng
- http://scikit-learn.org/stable/modules/sgd.html
- R packages
The error function from a simple linear regression looks like
- [math]\displaystyle{ \begin{align} Err(m,b) &= \frac{1}{N}\sum_{i=1}^n (y_i - (m x_i + b))^2, \\ \end{align} }[/math]
We compute the gradient first for each parameters.
- [math]\displaystyle{ \begin{align} \frac{\partial Err}{\partial m} &= \frac{2}{n} \sum_{i=1}^n -x_i(y_i - (m x_i + b)), \\ \frac{\partial Err}{\partial b} &= \frac{2}{n} \sum_{i=1}^n -(y_i - (m x_i + b)) \end{align} }[/math]
The gradient descent algorithm uses an iterative method to update the estimates using a tuning parameter called learning rate.
new_m &= m_current - (learningRate * m_gradient) new_b &= b_current - (learningRate * b_gradient)
After each iteration, derivative is closer to zero. Coding in R for the simple linear regression.
Gradient descent vs Newton's method
- What is the difference between Gradient Descent and Newton's Gradient Descent?
- Newton's Method vs Gradient Descent Method in tacking saddle points in Non-Convex Optimization
- Gradient Descent vs Newton Method
Double descent
Classification and Regression Trees (CART)
Construction of the tree classifier
- Node proportion
- [math]\displaystyle{ p(1|t) + \dots + p(6|t) =1 }[/math] where [math]\displaystyle{ p(j|t) }[/math] define the node proportions (class proportion of class j on node t. Here we assume there are 6 classes.
- Impurity of node t
- [math]\displaystyle{ i(t) }[/math] is a nonnegative function [math]\displaystyle{ \phi }[/math] of the [math]\displaystyle{ p(1|t), \dots, p(6|t) }[/math] such that [math]\displaystyle{ \phi(1/6,1/6,\dots,1/6) }[/math] = maximumm [math]\displaystyle{ \phi(1,0,\dots,0)=0, \phi(0,1,0,\dots,0)=0, \dots, \phi(0,0,0,0,0,1)=0 }[/math]. That is, the node impurity is largest when all classes are equally mixed together in it, and smallest when the node contains only one class.
- Gini index of impurity
- [math]\displaystyle{ i(t) = - \sum_{j=1}^6 p(j|t) \log p(j|t). }[/math]
- Goodness of the split s on node t
- [math]\displaystyle{ \Delta i(s, t) = i(t) -p_Li(t_L) - p_Ri(t_R). }[/math] where [math]\displaystyle{ p_R }[/math] are the proportion of the cases in t go into the left node [math]\displaystyle{ t_L }[/math] and a proportion [math]\displaystyle{ p_R }[/math] go into right node [math]\displaystyle{ t_R }[/math].
A tree was grown in the following way: At the root node [math]\displaystyle{ t_1 }[/math], a search was made through all candidate splits to find that split [math]\displaystyle{ s^* }[/math] which gave the largest decrease in impurity;
- [math]\displaystyle{ \Delta i(s^*, t_1) = \max_{s} \Delta i(s, t_1). }[/math]
- Class character of a terminal node was determined by the plurality rule. Specifically, if [math]\displaystyle{ p(j_0|t)=\max_j p(j|t) }[/math], then t was designated as a class [math]\displaystyle{ j_0 }[/math] terminal node.
R packages
- rpart
- http://exploringdatablog.blogspot.com/2013/04/classification-tree-models.html
- parttree: Visualize Simple 2-D Decision Tree Partitions
Partially additive (generalized) linear model trees
- https://eeecon.uibk.ac.at/~zeileis/news/palmtree/
- https://cran.r-project.org/web/packages/palmtree/index.html
Supervised Classification, Logistic and Multinomial
Variable selection
Review
Variable selection – A review and recommendations for the practicing statistician by Heinze et al 2018.
Variable selection and variable importance plot
Variable selection and cross-validation
- http://freakonometrics.hypotheses.org/19925
- http://ellisp.github.io/blog/2016/06/05/bootstrap-cv-strategies/
Mallow Cp
Mallows's Cp addresses the issue of overfitting. The Cp statistic calculated on a sample of data estimates the mean squared prediction error (MSPE).
- [math]\displaystyle{ E\sum_j (\hat{Y}_j - E(Y_j\mid X_j))^2/\sigma^2, }[/math]
The Cp statistic is defined as
- [math]\displaystyle{ C_p={SSE_p \over S^2} - N + 2P. }[/math]
- https://en.wikipedia.org/wiki/Mallows%27s_Cp
- Better and enhanced method of estimating Mallow's Cp
- Used in Yuan & Lin (2006) group lasso. The degrees of freedom is estimated by the bootstrap or perturbation methods. Their paper mentioned the performance is comparable with that of 5-fold CV but is computationally much faster.
Variable selection for mode regression
http://www.tandfonline.com/doi/full/10.1080/02664763.2017.1342781 Chen & Zhou, Journal of applied statistics ,June 2017
lmSubsets
lmSubsets: Exact variable-subset selection in linear regression. 2020
Permutation method
BASIC XAI with DALEX — Part 2: Permutation-based variable importance
Neural network
- Build your own neural network in R
- Building A Neural Net from Scratch Using R - Part 1
- (Video) 10.2: Neural Networks: Perceptron Part 1 - The Nature of Code from the Coding Train. The book THE NATURE OF CODE by DANIEL SHIFFMAN
- CLASSIFICATION FROM SCRATCH, NEURAL NETS. The ROCR package was used to produce the ROC curve.
- Building a survival-neuralnet from scratch in base R
Support vector machine (SVM)
- Improve SVM tuning through parallelism by using the foreach and doParallel packages.
- Plotting SVM Decision Boundaries with e1071 in R
Quadratic Discriminant Analysis (qda), KNN
Machine Learning. Stock Market Data, Part 3: Quadratic Discriminant Analysis and KNN
KNN
KNN Algorithm Machine Learning
Regularization
Regularization is a process of introducing additional information in order to solve an ill-posed problem or to prevent overfitting
Regularization: Ridge, Lasso and Elastic Net from datacamp.com. Bias and variance trade-off in parameter estimates was used to lead to the discussion.
Regularized least squares
https://en.wikipedia.org/wiki/Regularized_least_squares. Ridge/ridge/elastic net regressions are special cases.
Ridge regression
- What is ridge regression?
- Why does ridge estimate become better than OLS by adding a constant to the diagonal? The estimates become more stable if the covariates are highly correlated.
- (In ridge regression) the matrix we need to invert no longer has determinant near zero, so the solution does not lead to uncomfortably large variance in the estimated parameters. And that’s a good thing. See this post.
- Multicolinearity and ridge regression: results on type I errors, power and heteroscedasticity
Since L2 norm is used in the regularization, ridge regression is also called L2 regularization.
Hoerl and Kennard (1970a, 1970b) introduced ridge regression, which minimizes RSS subject to a constraint [math]\displaystyle{ \sum|\beta_j|^2 \le t }[/math]. Note that though ridge regression shrinks the OLS estimator toward 0 and yields a biased estimator [math]\displaystyle{ \hat{\beta} = (X^TX + \lambda X)^{-1} X^T y }[/math] where [math]\displaystyle{ \lambda=\lambda(t) }[/math], a function of t, the variance is smaller than that of the OLS estimator.
The solution exists if [math]\displaystyle{ \lambda \gt 0 }[/math] even if [math]\displaystyle{ n \lt p }[/math].
Ridge regression (L2 penalty) only shrinks the coefficients. In contrast, Lasso method (L1 penalty) tries to shrink some coefficient estimators to exactly zeros. This can be seen from comparing the coefficient path plot from both methods.
Geometrically (contour plot of the cost function), the L1 penalty (the sum of absolute values of coefficients) will incur a probability of some zero coefficients (i.e. some coefficient hitting the corner of a diamond shape in the 2D case). For example, in the 2D case (X-axis=[math]\displaystyle{ \beta_0 }[/math], Y-axis=[math]\displaystyle{ \beta_1 }[/math]), the shape of the L1 penalty [math]\displaystyle{ |\beta_0| + |\beta_1| }[/math] is a diamond shape whereas the shape of the L2 penalty ([math]\displaystyle{ \beta_0^2 + \beta_1^2 }[/math]) is a circle.
Lasso/glmnet, adaptive lasso and FAQs
Lasso logistic regression
https://freakonometrics.hypotheses.org/52894
Lagrange Multipliers
A Simple Explanation of Why Lagrange Multipliers Works
How to solve lasso/convex optimization
- Convex Optimization by Boyd S, Vandenberghe L, Cambridge 2004. It is cited by Zhang & Lu (2007). The interior point algorithm can be used to solve the optimization problem in adaptive lasso.
- Review of gradient descent:
- Finding maximum: [math]\displaystyle{ w^{(t+1)} = w^{(t)} + \eta \frac{dg(w)}{dw} }[/math], where [math]\displaystyle{ \eta }[/math] is stepsize.
- Finding minimum: [math]\displaystyle{ w^{(t+1)} = w^{(t)} - \eta \frac{dg(w)}{dw} }[/math].
- What is the difference between Gradient Descent and Newton's Gradient Descent? Newton's method requires [math]\displaystyle{ g''(w) }[/math], more smoothness of g(.).
- Finding minimum for multiple variables (gradient descent): [math]\displaystyle{ w^{(t+1)} = w^{(t)} - \eta \Delta g(w^{(t)}) }[/math]. For the least squares problem, [math]\displaystyle{ g(w) = RSS(w) }[/math].
- Finding minimum for multiple variables in the least squares problem (minimize [math]\displaystyle{ RSS(w) }[/math]): [math]\displaystyle{ \text{partial}(j) = -2\sum h_j(x_i)(y_i - \hat{y}_i(w^{(t)}), w_j^{(t+1)} = w_j^{(t)} - \eta \; \text{partial}(j) }[/math]
- Finding minimum for multiple variables in the ridge regression problem (minimize [math]\displaystyle{ RSS(w)+\lambda \|w\|_2^2=(y-Hw)'(y-Hw)+\lambda w'w }[/math]): [math]\displaystyle{ \text{partial}(j) = -2\sum h_j(x_i)(y_i - \hat{y}_i(w^{(t)}), w_j^{(t+1)} = (1-2\eta \lambda) w_j^{(t)} - \eta \; \text{partial}(j) }[/math]. Compared to the closed form approach: [math]\displaystyle{ \hat{w} = (H'H + \lambda I)^{-1}H'y }[/math] where 1. the inverse exists even N<D as long as [math]\displaystyle{ \lambda \gt 0 }[/math] and 2. the complexity of inverse is [math]\displaystyle{ O(D^3) }[/math], D is the dimension of the covariates.
- Cyclical coordinate descent was used (vignette) in the glmnet package. See also coordinate descent. The reason we call it 'descent' is because we want to 'minimize' an objective function.
- [math]\displaystyle{ \hat{w}_j = \min_w g(\hat{w}_1, \cdots, \hat{w}_{j-1},w, \hat{w}_{j+1}, \cdots, \hat{w}_D) }[/math]
- See paper on JSS 2010. The Cox PHM case also uses the cyclical coordinate descent method; see the paper on JSS 2011.
- Coursera's Machine learning course 2: Regression at 1:42. Soft-thresholding the coefficients is the key for the L1 penalty. The range for the thresholding is controlled by [math]\displaystyle{ \lambda }[/math]. Note to view the videos and all materials in coursera we can enroll to audit the course without starting a trial.
- Introduction to Coordinate Descent using Least Squares Regression. It also covers Cyclic Coordinate Descent and Coordinate Descent vs Gradient Descent. A python code is provided.
- No step size is required as in gradient descent.
- Implementing LASSO Regression with Coordinate Descent, Sub-Gradient of the L1 Penalty and Soft Thresholding in Python
- Coordinate descent in the least squares problem: [math]\displaystyle{ \frac{\partial}{\partial w_j} RSS(w)= -2 \rho_j + 2 w_j }[/math]; i.e. [math]\displaystyle{ \hat{w}_j = \rho_j }[/math].
- Coordinate descent in the Lasso problem (for normalized features): [math]\displaystyle{ \hat{w}_j = \begin{cases} \rho_j + \lambda/2, & \text{if }\rho_j \lt -\lambda/2 \\ 0, & \text{if } -\lambda/2 \le \rho_j \le \lambda/2\\ \rho_j- \lambda/2, & \text{if }\rho_j \gt \lambda/2 \end{cases} }[/math]
- Choosing [math]\displaystyle{ \lambda }[/math] via cross validation tends to favor less sparse solutions and thus smaller [math]\displaystyle{ \lambda }[/math] then optimal choice for feature selection. See "Machine learning: a probabilistic perspective", Murphy 2012.
- Lasso Regularization for Generalized Linear Models in Base SAS® Using Cyclical Coordinate Descent
- Classical: Least angle regression (LARS) Efron et al 2004.
- Alternating Direction Method of Multipliers (ADMM). Boyd, 2011. “Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers.” Foundations and Trends in Machine Learning. Vol. 3, No. 1, 2010, pp. 1–122.
- If some variables in design matrix are correlated, then LASSO is convex or not?
- Tibshirani. Regression shrinkage and selection via the lasso (free). JRSS B 1996.
- Convex Optimization in R by Koenker & Mizera 2014.
- Pathwise coordinate optimization by Friedman et al 2007.
- Statistical learning with sparsity: the Lasso and generalizations T. Hastie, R. Tibshirani, and M. Wainwright, 2015 (book)
- Element of Statistical Learning (book)
- https://youtu.be/A5I1G1MfUmA StatsLearning Lect8h 110913
- Fu's (1998) shooting algorithm for Lasso (mentioned in the history of coordinate descent) and Zhang & Lu's (2007) modified shooting algorithm for adaptive Lasso.
- Machine Learning: a Probabilistic Perspective Choosing [math]\displaystyle{ \lambda }[/math] via cross validation tends to favor less sparse solutions and thus smaller [math]\displaystyle{ \lambda }[/math] than optimal choice for feature selection.
- Cyclops package - Cyclic Coordinate Descent for Logistic, Poisson and Survival Analysis. CRAN. It imports Rcpp package. It also provides Dockerfile.
- Coordinate Descent Algorithms by Stephen J. Wright
Quadratic programming
- https://en.wikipedia.org/wiki/Quadratic_programming
- https://en.wikipedia.org/wiki/Lasso_(statistics)
- CRAN Task View: Optimization and Mathematical Programming
- quadprog package and solve.QP() function
- Solving Quadratic Progams with R’s quadprog package
- More on Quadratic Programming in R
- https://optimization.mccormick.northwestern.edu/index.php/Quadratic_programming
- Maximin projection learning for optimal treatment decision with heterogeneous individualized treatment effects where the algorithm from Lee 2016 was used.
Constrained optimization
Jaya Package. Jaya Algorithm is a gradient-free optimization algorithm. It can be used for Maximization or Minimization of a function for solving both constrained and unconstrained optimization problems. It does not contain any hyperparameters.
1. Elastic net
2. Group lasso
- Yuan and Lin 2006 JRSSB
- https://cran.r-project.org/web/packages/gglasso/, http://royr2.github.io/2014/04/15/GroupLasso.html
- https://cran.r-project.org/web/packages/grpreg/
- https://cran.r-project.org/web/packages/grplasso/ by Lukas Meier (paper), used in the biospear package for survival data
- https://cran.r-project.org/web/packages/SGL/index.html, http://royr2.github.io/2014/05/20/SparseGroupLasso.html, http://web.stanford.edu/~hastie/Papers/SGLpaper.pdf
Grouped data
Other Lasso
- pcLasso
- A Fast and Flexible Algorithm for Solving the Lasso in Large-scale and Ultrahigh-dimensional Problems Qian et al 2019 and the snpnet package
- Adaptive penalization in high-dimensional regression and classification with external covariates using variational Bayes by Velten & Huber 2019 and the bioconductor package graper. Differentially penalizes feature groups defined by the covariates and adapts the relative strength of penalization to the information content of each group. Incorporating side-information on the assay type and spatial or functional annotations could help to improve prediction performance. Furthermore, it could help prioritizing feature groups, such as different assays or gene sets.
Comparison by plotting
If we are running simulation, we can use the DALEX package to visualize the fitting result from different machine learning methods and the true model. See http://smarterpoland.pl/index.php/2018/05/ml-models-what-they-cant-learn.
Prediction
Prediction, Estimation, and Attribution Efron 2020
Postprediction inference/Inference based on predicted outcomes
Methods for correcting inference based on outcomes predicted by machine learning Wang 2020. postpi package.
SHAP/SHapley Additive exPlanation: feature importance for each class
- https://en.wikipedia.org/wiki/Shapley_value
- Python https://shap.readthedocs.io/en/latest/index.html
- Introduction to SHAP with Python. For a given prediction, SHAP values can tell us how much each factor in a model has contributed to the prediction.
- A Novel Approach to Feature Importance — Shapley Additive Explanations
- SHAP: Shapley Additive Explanations
- R package shapr: Prediction Explanation with Dependence-Aware Shapley Values
- The output of Shapley value produced by explain() is an n_test x (1+p_test) matrix where "n" is the number of obs and "p" is the dimension of predictor.
- The Shapley values can be plotted using a barplot for each test sample.
- approach parameter can be empirical/gaussian/copula/ctree. See doc
- Note the package only supports a few prediction models to be used in the shapr function.
$ debug(shapr:::get_supported_models) $ shapr:::get_supported_models() Browse[2]> print(DT) model_class get_model_specs predict_model 1: default FALSE TRUE 2: gam TRUE TRUE 3: glm TRUE TRUE 4: lm TRUE TRUE 5: ranger TRUE TRUE 6: xgb.Booster TRUE TRUE
- A gentle introduction to SHAP values in R xgboost package
- Create SHAP plots for tidymodels objects
- shapper: Wrapper of Python Library 'shap'
- Interpret Complex Linear Models with SHAP within Seconds
- SHAP Values of Additive Models
- Key improvements in shapviz and kernelshap
Imbalanced/unbalanced Classification
See ROC.
Deep Learning
- CS294-129 Designing, Visualizing and Understanding Deep Neural Networks from berkeley.
- https://www.youtube.com/playlist?list=PLkFD6_40KJIxopmdJF_CLNqG3QuDFHQUm
- Deep Learning from first principles in Python, R and Octave – Part 5
Tensor Flow (tensorflow package)
- https://tensorflow.rstudio.com/
- Machine Learning with R and TensorFlow (Video)
- Machine Learning Crash Course with TensorFlow APIs
- Predicting cancer outcomes from histology and genomics using convolutional networks Pooya Mobadersany et al, PNAS 2018
Biological applications
Machine learning resources
- These Machine Learning Courses Will Prepare a Career Path for You
- 101 Machine Learning Algorithms for Data Science with Cheat Sheets
- Supervised machine learning case studies in R - A Free, Interactive Course Using Tidy Tools.
The Bias-Variance Trade-Off & "DOUBLE DESCENT" in the test error
https://twitter.com/daniela_witten/status/1292293102103748609 and an easy to read Thread Reader.
- (Thread #17) The key point is with 20 DF, n=p, and there's exactly ONE least squares fit that has zero training error. And that fit happens to have oodles of wiggles.....
- (Thread #18) but as we increase the DF so that p>n, there are TONS of interpolating least squares fits. The MINIMUM NORM least squares fit is the "least wiggly" of those zillions of fits. And the "least wiggly" among them is even less wiggly than the fit when p=n !!!
- (Thread #19) "double descent" is happening b/c DF isn't really the right quantity for the the x-axis: like, the fact that we are choosing the minimum norm least squares fit actually means that the spline with 36 DF is **less** flexible than the spline with 20 DF.
- (Thread #20) if had used a ridge penalty when fitting the spline (instead of least squares)? Well then we wouldn't have interpolated training set, we wouldn't have seen double descent, AND we would have gotten better test error (for the right value of the tuning parameter!)
- (Thread #21) When we use (stochastic) gradient descent to fit a neural net, we are actually picking out the minimum norm solution!! So the spline example is a pretty good analogy for what is happening when we see double descent for neural nets.
Survival data
Deep learning for survival outcomes Steingrimsson, 2020
Randomization inference
- Google: randomization inference in r
- Randomization Inference for Outcomes with Clumping at Zero, The American Statistician 2018
- Randomization inference vs. bootstrapping for p-values
Randomization test
Myths of randomisation
Unequal probabilities
Sampling without replacement with unequal probabilities
Model selection criteria
- Assessing the Accuracy of our models (R Squared, Adjusted R Squared, RMSE, MAE, AIC)
- Comparing additive and multiplicative regressions using AIC in R
- Model Selection and Regression t-Statistics Derryberry 2019
- Mean Absolute Deviance. Measure of the average absolute difference between the predicted values and the actual values.
- Cf: Mean absolute deviation, Median absolute deviation. Measure of the variability.
All models are wrong
All models are wrong from George Box.
MSE
Akaike information criterion/AIC
- [math]\displaystyle{ \mathrm{AIC} \, = \, 2k - 2\ln(\hat L) }[/math], where k be the number of estimated parameters in the model.
- Smaller is better (error criteria)
- Akaike proposed to approximate the expectation of the cross-validated log likelihood [math]\displaystyle{ E_{test}E_{train} [log L(x_{test}| \hat{\beta}_{train})] }[/math] by [math]\displaystyle{ log L(x_{train} | \hat{\beta}_{train})-k }[/math].
- Leave-one-out cross-validation is asymptotically equivalent to AIC, for ordinary linear regression models.
- AIC can be used to compare two models even if they are not hierarchically nested.
- AIC() from the stats package.
- broom::glance() was used.
- Generally resampling based measures such as cross-validation should be preferred over theoretical measures such as Aikake's Information Criteria. Understanding the Bias-Variance Tradeoff & Accurately Measuring Model Prediction Error.
BIC
- [math]\displaystyle{ \mathrm{BIC} \, = \, \ln(n) \cdot 2k - 2\ln(\hat L) }[/math], where k be the number of estimated parameters in the model.
Overfitting
- How to judge if a supervised machine learning model is overfitting or not?
- The Nature of Overfitting, Smoothing isn’t Always Safe
AIC vs AUC
What is the difference in what AIC and c-statistic (AUC) actually measure for model fit?
Roughly speaking:
- AIC is telling you how good your model fits for a specific mis-classification cost.
- AUC is telling you how good your model would work, on average, across all mis-classification costs.
Frank Harrell: AUC (C-index) has the advantage of measuring the concordance probability as you stated, aside from cost/utility considerations. To me the bottom line is the AUC should be used to describe discrimination of one model, not to compare 2 models. For comparison we need to use the most powerful measure: deviance and those things derived from deviance: generalized 𝑅2 and AIC.
Variable selection and model estimation
Proper variable selection: Use only training data or full data?
- training observations to perform all aspects of model-fitting—including variable selection
- make use of the full data set in order to obtain more accurate coefficient estimates (This statement is arguable)
Cross-Validation
References:
R packages:
- rsample (released July 2017). An example from the postpi package.
- CrossValidate (released July 2017)
- crossval (github, new home at https://techtonique.r-universe.dev/),
Bias–variance tradeoff
- Wikipedia
- Everything You Need To Know About Bias And Variance. Y-axis = error, X-axis = model complexity.
- Statistics - Bias-variance trade-off (between overfitting and underfitting)
- *Chapter 4 The Bias–Variance Tradeoff from Basics of Statistical Learning by David Dalpiaz. R code is included. Regression case.
- Ridge regression
- [math]\displaystyle{ Obj = (y-X \beta)^T (y - X \beta) + \lambda ||\beta||_2^2 }[/math]
- Plot of MSE, bias**2, variance of ridge estimator in terms of lambda by Léo Belzile. Note that there is a typo in the bias term. It should be [math]\displaystyle{ E(\gamma)-\gamma = [(Z^TZ+\lambda I_p)^{-1}Z^TZ -I_p] \lambda }[/math].
- Explicit form of the bias and variance of ridge estimator. The estimator is linear. [math]\displaystyle{ \hat{\beta} = (X^T X + \lambda I_p)^{-1} (X^T y) }[/math]
Data splitting
PRESS statistic (LOOCV) in regression, Predicted R²
- The PRESS statistic (predicted residual error sum of squares) [math]\displaystyle{ \sum_i (y_i - \hat{y}_{i,-i})^2 }[/math] provides another way to find the optimal model in regression.
See the formula for the ridge regression case.
LOOCV vs 10-fold CV in classification
- Background: Variance of mean for correlated data. If the variables have equal variance σ2 and the average correlation of distinct variables is ρ, then the variance of their mean is
- [math]\displaystyle{ \operatorname{Var}\left(\overline{X}\right) = \frac{\sigma^2}{n} + \frac{n - 1}{n}\rho\sigma^2. }[/math]
- This implies that the variance of the mean increases with the average of the correlations.
- (5.1.4 of ISLR 2nd)
- k-fold CV is that it often gives more accurate estimates of the test error rate than does LOOCV. This has to do with a bias-variance trade-off.
- When we perform LOOCV, we are in effect averaging the outputs of n fitted models, each of which is trained on an almost identical set of observations; therefore, these outputs are highly (positively) correlated with each other. Since the mean of many highly correlated quantities has higher variance than does the mean of many quantities that are not as highly correlated, the test error estimate resulting from LOOCV tends to have higher variance than does the test error estimate resulting from k-fold CV... Typically, given these considerations, one performs k-fold cross-validation using k = 5 or k = 10, as these values have been shown empirically to yield test error rate estimates that suffer neither from excessively high bias nor from very high variance.
- 10-fold Cross-validation vs leave-one-out cross-validation
- Leave-one-out cross-validation is approximately unbiased. But it tends to have a high variance.
- The variance in fitting the model tends to be higher if it is fitted to a small dataset.
- In LOOCV, because there is a lot of overlap between training sets, and thus the test error estimates are highly correlated, which means that the mean value of the test error estimate will have higher variance.
- Unless the dataset were very small, I would use 10-fold cross-validation if it fitted in my computational budget, or better still, bootstrap estimation and bagging.
- Chapter 5 Resampling Methods of ISLR 2nd.
- Bias-Variance Tradeoff and k-fold Cross-Validation
- Why is leave-one-out cross-validation (LOOCV) variance about the mean estimate for error high?
- High variance of leave-one-out cross-validation
- Prediction Error Estimation: A Comparison of Resampling Methods Molinaro 2005
- Survival data An evaluation of resampling methods for assessment of survival risk prediction in high-dimensional settings Subramanian 2010
- Using cross-validation to evaluate predictive accuracy of survival risk classifiers based on high-dimensional data Subramanian 2011.
- classification error: (Molinaro 2005) For small sample sizes of fewer than 50 cases, they recommended use of leave-one-out cross-validation to minimize mean squared error of the estimate of prediction error.
- survival data using time-dependent ROC: (Subramanian 2010) They recommended use of 5- or 10-fold cross-validation for a wide range of conditions
Monte carlo cross-validation
This method creates multiple random splits of the dataset into training and validation data. See Wikipedia.
- It is not creating replicates of CV samples.
- As the number of random splits approaches infinity, the result of repeated random sub-sampling validation tends towards that of leave-p-out cross-validation.
Difference between CV & bootstrapping
Differences between cross validation and bootstrapping to estimate the prediction error
- CV tends to be less biased but K-fold CV has fairly large variance.
- Bootstrapping tends to drastically reduce the variance but gives more biased results (they tend to be pessimistic).
- The 632 and 632+ rules methods have been adapted to deal with the bootstrap bias
- Repeated CV does K-fold several times and averages the results similar to regular K-fold
.632 and .632+ bootstrap
- 0.632 bootstrap: Efron's paper Estimating the Error Rate of a Prediction Rule: Improvement on Cross-Validation in 1983.
- 0.632+ bootstrap: The CV estimate of prediction error is nearly unbiased but can be highly variable. See Improvements on Cross-Validation: The .632+ Bootstrap Method by Efron and Tibshirani, JASA 1997.
- Chap 17.7 from "An Introduction to the Bootstrap" by Efron and Tibshirani. Chapman & Hall.
- Chap 7.4 (resubstitution error [math]\displaystyle{ \overline{err} }[/math]) and chap 7.11 ([math]\displaystyle{ Err_{boot(1)} }[/math]leave-one-out bootstrap estimate of prediction error) from "The Elements of Statistical Learning" by Hastie, Tibshirani and Friedman. Springer.
- What is the .632 bootstrap?
- [math]\displaystyle{ Err_{.632} = 0.368 \overline{err} + 0.632 Err_{boot(1)} }[/math]
- Bootstrap, 0.632 Bootstrap, 0.632+ Bootstrap from Encyclopedia of Systems Biology by Springer.
- bootpred() from bootstrap function.
- The .632 bootstrap estimate can be extended to statistics other than prediction error. See the paper Issues in developing multivariable molecular signatures for guiding clinical care decisions by Sachs. Source code. Let [math]\displaystyle{ \phi }[/math] be a performance metric, [math]\displaystyle{ S_b }[/math] a sample of size n from a bootstrap, [math]\displaystyle{ S_{-b} }[/math] subset of [math]\displaystyle{ S }[/math] that is disjoint from [math]\displaystyle{ S_b }[/math]; test set.
- [math]\displaystyle{ \hat{E}^*[\phi_{\mathcal{F}}(S)] = .368 \hat{E}[\phi_{f}(S)] + 0.632 \hat{E}[\phi_{f_b}(S_{-b})] }[/math]
- where [math]\displaystyle{ \hat{E}[\phi_{f}(S)] }[/math] is the naive estimate of [math]\displaystyle{ \phi_f }[/math] using the entire dataset.
- For survival data
- ROC632 package, Overview, and the paper Time Dependent ROC Curves for the Estimation of True Prognostic Capacity of Microarray Data by Founcher 2012.
- Efron-Type Measures of Prediction Error for Survival Analysis Gerds 2007.
- Assessment of survival prediction models based on microarray data Schumacher 2007. Brier score.
- Evaluating Random Forests for Survival Analysis using Prediction Error Curves Mogensen, 2012. pec package
- Assessment of performance of survival prediction models for cancer prognosis Chen 2012. Concordance, ROC... But bootstrap was not used.
- Comparison of Cox Model Methods in A Low-dimensional Setting with Few Events 2016. Concordance, calibration slopes RMSE are considered.
Create partitions for cross-validation
Stratified sampling: caret::createFolds() or rsample::vfold_cv (used in tidymodels specifically)
- set.seed(), sample.split(),createDataPartition(), and createFolds() functions from the caret package. Simple Splitting with Important Groups. ?createFolds, Stratified K-folds Cross-Validation with Caret
# Stratified sampling library(caret) set.seed(1) x <- sample(rep(c("A", "B"), c(100, 200))) # 1:2 ratio folds <- createFolds(x, k = 5, list = TRUE, returnTrain = FALSE) # Confirm that each fold has approximately the same proportion of samples # for each unique value in the target variable for(i in 1:5) print(prop.table(table(x[folds[[i]]]))) # 1:2 ratio length(unique(union(union(union(union(folds[[1]], folds[[2]]), folds[[3]]), folds[[4]]), folds[[5]]))) # [1] 300library(rsample) # Stratified 5-fold CV on iris data cv_rs <- vfold_cv(iris, v = 5, strata = Species) # First fold train1 <- analysis(cv_rs$splits[[1]]) test1 <- assessment(cv_rs$splits[[1]]) table(train1$Species) table(test1$Species)
Random sampling: sample()
- cv.glmnet()
sample(rep(seq(nfolds), length = N)) # a vector set.seed(1); sample(rep(seq(3), length = 20)) # [1] 1 1 1 2 1 1 2 2 2 3 3 2 3 1 3 3 3 1 2 2
- Another way is to use replace=TRUE in sample() (not quite uniform compared to the last method, strange)
sample(1:nfolds, N, replace=TRUE) # a vector set.seed(1); sample(1:3, 20, replace=TRUE) # [1] 1 3 1 2 1 3 3 2 2 3 3 1 1 1 2 2 2 2 3 1 table(.Last.value) # .Last.value # 1 2 3 # 7 7 6
- k-fold cross validation with modelr and broom
- h2o package to split the merged training dataset into three parts
n <- 42; nfold <- 5 # unequal partition folds <- split(sample(1:n), rep(1:nfold, length = n)) # a list sapply(folds, length)
- Another simple example. Split the data into 70% training data and 30% testing data
mysplit <- sample(c(rep(0, 0.7 * nrow(df)), rep(1, nrow(df) - 0.7 * nrow(df)))) train <- df[mysplit == 0, ] test <- df[mysplit == 1, ]
Create training/testing data
- ?createDataPartition.
- caret createDataPartition returns more samples than expected. It is more complicated than it looks.
set.seed(1) createDataPartition(rnorm(10), p=.3) # $Resample1 # [1] 1 2 4 5 set.seed(1) createDataPartition(rnorm(10), p=.5) # $Resample1 # [1] 1 2 4 5 6 9
- Stratified Sampling in R: A Practical Guide with Base R and dplyr
- Stratified sampling: Stratified Sampling in R (With Examples), initial_split() from tidymodels. With a strata argument, the random sampling is conducted within the stratification variable. So it guaranteed each strata (stratify variable level) has observations in training and testing sets.
> library(rsample) # or library(tidymodels) > table(mtcars$cyl) 4 6 8 11 7 14 > set.seed(22) > sp <- initial_split(mtcars, prop=.8, strata = cyl) # 80% training and 20% testing sets > table(training(sp)$cyl) 4 6 8 8 5 11 > table(testing(sp)$cyl) 4 6 8 3 2 3 > 8/11; 5/7; 11/14 # split by initial_split() [1] 0.7272727 [1] 0.7142857 [1] 0.7857143 > 9/11; 6/7; 12/14 # if we try to increase 1 observation [1] 0.8181818 [1] 0.8571429 [1] 0.8571429 > (8+5+11)/nrow(mtcars) [1] 0.75 > (9+6+12)/nrow(mtcars) [1] 0.84375 # looks better > set.seed(22) > sp2 <- initial_split(mtcars, prop=.8) table(training(sp2)$cyl) 4 6 8 8 7 10 > table(testing(sp2)$cyl) 4 8 3 4 # not what we want since cyl "6" has no observations
Nested resampling
- Nested Resampling with rsample
- Introduction to Machine Learning (I2ML)
- https://stats.stackexchange.com/questions/292179/whats-the-meaning-of-nested-resampling
Nested resampling is need when we want to tuning a model by using a grid search. The default settings of a model are likely not optimal for each data set out. So an inner CV has to be performed with the aim to find the best parameter set of a learner for each fold.
See a diagram at https://i.stack.imgur.com/vh1sZ.png
In BRB-ArrayTools -> class prediction with multiple methods, the alpha (significant level of threshold used for gene selection, 2nd option in individual genes) can be viewed as a tuning parameter for the development of a classifier.
Pre-validation/pre-validated predictor
- Pre-validation and inference in microarrays Tibshirani and Efron, Statistical Applications in Genetics and Molecular Biology, 2002.
- See glmnet vignette
- http://www.stat.columbia.edu/~tzheng/teaching/genetics/papers/tib_efron.pdf#page=5. In each CV, we compute the estimate of the response. This estimate of the response will serve as a new predictor (pre-validated 'predictor' ) in the final fitting model.
- P1101 of Sachs 2016. With pre-validation, instead of computing the statistic [math]\displaystyle{ \phi }[/math] for each of the held-out subsets ([math]\displaystyle{ S_{-b} }[/math] for the bootstrap or [math]\displaystyle{ S_{k} }[/math] for cross-validation), the fitted signature [math]\displaystyle{ \hat{f}(X_i) }[/math] is estimated for [math]\displaystyle{ X_i \in S_{-b} }[/math] where [math]\displaystyle{ \hat{f} }[/math] is estimated using [math]\displaystyle{ S_{b} }[/math]. This process is repeated to obtain a set of pre-validated 'signature' estimates [math]\displaystyle{ \hat{f} }[/math]. Then an association measure [math]\displaystyle{ \phi }[/math] can be calculated using the pre-validated signature estimates and the true outcomes [math]\displaystyle{ Y_i, i = 1, \ldots, n }[/math].
- Another description from the paper The Spike-and-Slab Lasso Generalized Linear Models for Prediction and Associated Genes Detection. The prevalidation method is a variant of cross-validation. We then use [math]\displaystyle{ (y_i, \hat{\eta}_i) }[/math] to compute the measures described above. The cross-validated linear predictor for each patient is derived independently of the observed response of the patient, and hence the “prevalidated” dataset Embedded Image can essentially be treated as a “new dataset.” Therefore, this procedure provides valid assessment of the predictive performance of the model. To get stable results, we run 10× 10-fold cross-validation for real data analysis.
- In CV, left-out samples = hold-out cases = test set
Custom cross validation
- vtreat package
- https://github.com/WinVector/vtreat/blob/master/Examples/CustomizedCrossPlan/CustomizedCrossPlan.md
Cross validation vs regularization
When Cross-Validation is More Powerful than Regularization
Cross-validation with confidence (CVC)
JASA 2019 by Jing Lei, pdf, code
Correlation data
Cross-Validation for Correlated Data Rabinowicz, JASA 2020
Bias in Error Estimation
- Pitfalls in the Use of DNA Microarray Data for Diagnostic and Prognostic Classification Simon 2003. My R code.
- Conclusion: Feature selection must be done within each cross-validation. Otherwise the selected feature already saw the labels of the training data, and made use of them.
- Simulation: 2000 sets of 20 samples, of which 10 belonged to class 1 and the remaining 10 to class 2. Each sample was a vector of 6000 features (synthetic gene expressions).
- Bias in Error Estimation when Using Cross-Validation for Model Selection Varma & Simon 2006
- Conclusion: Parameter tuning must be done within each cross-validation; nested CV is advocated.
- Figures 1 (Shrunken centroids, shrinkage parameter Δ) & 2 (SVM, kernel parameters) are biased. Figure 3 (Shrunken centroids) & 4 (SVM) are unbiased.
- For k-NN, the parameter is k.
- Simulation:
- Null data: 1000 sets of 40 samples, of which 20 belonged to class 1 and the remaining 20 to class 2. Each sample was a vector of 6000 features (synthetic gene expressions).
- Non-null data: we simulated differential expression by fixing 10 genes (out of 6000) to have a population mean differential expression of 1 between the two classes.
- Over-fitting and selection bias; see Cross-validation_(statistics), Selection bias on Wikipedia. Comic.
- On the cross-validation bias due to unsupervised pre-processing Moscovich, 2019. JRSSB 2022
- Risk of bias of prognostic models developed using machine learning: a systematic review in oncology Dhiman 2022
- Avoiding Overfitting from fastStat: All of REAL Statistics
Bias due to unsupervised preprocessing
On the cross-validation bias due to unsupervised preprocessing 2022. Below I follow the practice from Biowulf to install Mamba. In this example, the 'project1' subfolder (2.0 GB) is located in '~/conda/envs' directory.
$ which python3 /usr/bin/python3 $ wget https://github.com/conda-forge/miniforge/releases/latest/download/Mambaforge-Linux-x86_64.sh $ bash Mambaforge-Linux-x86_64.sh -p /home/brb/conda -b $ source ~/conda/etc/profile.d/conda.sh && source ~/conda/etc/profile.d/mamba.sh $ mkdir -p ~/bin $ cat <<'__EOF__' > ~/bin/myconda __conda_setup="$('/home/$USER/conda/bin/conda' 'shell.bash' 'hook' 2> /dev/null)" if [ $? -eq 0 ]; then eval "$__conda_setup" else if [ -f "/home/$USER/conda/etc/profile.d/conda.sh" ]; then . "/home/$USER/conda/etc/profile.d/conda.sh" else export PATH="/home/$USER/conda/bin:$PATH" fi fi unset __conda_setup if [ -f "/home/$USER/conda/etc/profile.d/mamba.sh" ]; then . "/home/$USER/conda/etc/profile.d/mamba.sh" fi __EOF__ $ source ~/bin/myconda $ export MAMBA_NO_BANNER=1 $ mamba create -n project1 python=3.7 numpy scipy scikit-learn mkl-service mkl_random pandas matplotlib $ mamba activate project1 $ which python # /home/brb/conda/envs/project1/bin/python $ git clone https://github.com/mosco/unsupervised-preprocessing.git $ cd unsupervised-preprocessing/ $ python # Ctrl+d to quit $ mamba deactivate
Pitfalls of applying machine learning in genomics
Navigating the pitfalls of applying machine learning in genomics 2022
Bootstrap
See Bootstrap
Clustering
See Clustering.
Cross-sectional analysis
- https://en.wikipedia.org/wiki/Cross-sectional_study. The opposite of cross-sectional analysis is longitudinal analysis.
- Cross-sectional analysis refers to a type of research method in which data is collected at a single point in time from a group of individuals, organizations, or other units of analysis. This approach contrasts with longitudinal studies, which follow the same group of individuals or units over an extended period of time.
- In a cross-sectional analysis, researchers typically collect data from a sample of individuals or units that are representative of the population of interest. This data can then be used to examine patterns, relationships, or differences among the units at a specific point in time.
- Cross-sectional analysis is commonly used in fields such as sociology, psychology, public health, and economics to study topics such as demographics, health behaviors, income inequality, and social attitudes. While cross-sectional analysis can provide valuable insights into the characteristics of a population at a given point in time, it cannot establish causality or determine changes over time.
Mixed Effect Model
Entropy
- [math]\displaystyle{ \begin{align} Entropy &= \sum \log(1/p(x)) p(x) = \sum Surprise P(Surprise) \end{align} }[/math]
Definition
Entropy is defined by -log2(p) where p is a probability. Higher entropy represents higher unpredictable of an event.
Some examples:
- Fair 2-side die: Entropy = -.5*log2(.5) - .5*log2(.5) = 1.
- Fair 6-side die: Entropy = -6*1/6*log2(1/6) = 2.58
- Weighted 6-side die: Consider pi=.1 for i=1,..,5 and p6=.5. Entropy = -5*.1*log2(.1) - .5*log2(.5) = 2.16 (less unpredictable than a fair 6-side die).
Use
When entropy was applied to the variable selection, we want to select a class variable which gives a largest entropy difference between without any class variable (compute entropy using response only) and with that class variable (entropy is computed by adding entropy in each class level) because this variable is most discriminative and it gives most information gain. For example,
- entropy (without any class)=.94,
- entropy(var 1) = .69,
- entropy(var 2)=.91,
- entropy(var 3)=.725.
We will choose variable 1 since it gives the largest gain (.94 - .69) compared to the other variables (.94 -.91, .94 -.725).
Why is picking the attribute with the most information gain beneficial? It reduces entropy, which increases predictability. A decrease in entropy signifies an decrease in unpredictability, which also means an increase in predictability.
Consider a split of a continuous variable. Where should we cut the continuous variable to create a binary partition with the highest gain? Suppose cut point c1 creates an entropy .9 and another cut point c2 creates an entropy .1. We should choose c2.
Related
In addition to information gain, gini (dʒiːni) index is another metric used in decision tree. See wikipedia page about decision tree learning.
Ensembles
- Combining classifiers. Pro: better classification performance. Con: time consuming.
- Comic http://flowingdata.com/2017/09/05/xkcd-ensemble-model/
- Common Ensemble Models can be Biased
- pre: an R package for deriving prediction rule ensembles. It works on binary, multinomial, (multivariate) continuous, count and survival responses.
Bagging
Draw N bootstrap samples and summary the results (averaging for regression problem, majority vote for classification problem). Decrease variance without changing bias. Not help much with underfit or high bias models.
Random forest
- Variance importance: if you scramble the values of a variable, and the accuracy of your tree does not change much, then the variable is not very important.
- Why is it useful to compute variance importance? So the model's predictions are easier to interpret (not improve the prediction performance).
- Random forest has advantages of easier to run in parallel and suitable for small n large p problems.
- Random forest versus logistic regression: a large-scale benchmark experiment by Raphael Couronné, BMC Bioinformatics 2018
- Arborist: Parallelized, Extensible Random Forests
- On what to permute in test-based approaches for variable importance measures in Random Forests
- Tree Based Methods: Exploring the Forest A study of the different tree based methods in machine learning .
- It seems RF is good in classification problem. Comparing cross-validation results using crossval_ml and boxplots
- Random forests for the analysis of matched case–control studies 2024
Boosting
Instead of selecting data points randomly with the boostrap, it favors the misclassified points.
Algorithm:
- Initialize the weights
- Repeat
- resample with respect to weights
- retrain the model
- recompute weights
Since boosting requires computation in iterative and bagging can be run in parallel, bagging has an advantage over boosting when the data is very large.
Time series
- Ensemble learning for time series forecasting in R
- Time Series Forecasting Lab (Part 5) - Ensembles, Time Series Forecasting Lab (Part 6) - Stacked Ensembles
p-values
p-values
- Prob(Data | H0)
- https://en.wikipedia.org/wiki/P-value
- Statistical Inference in the 21st Century: A World Beyond p < 0.05 The American Statistician, 2019
- THE ASA SAYS NO TO P-VALUES The problem is that with large samples, significance tests pounce on tiny, unimportant departures from the null hypothesis. We have the opposite problem with small samples: The power of the test is low, and we will announce that there is “no significant effect” when in fact we may have too little data to know whether the effect is important.
- It’s not the p-values’ fault
- Exploring P-values with Simulations in R from Stable Markets.
- p-value and effect size. http://journals.sagepub.com/doi/full/10.1177/1745691614553988
- Ditch p-values. Use Bootstrap confidence intervals instead
Misuse of p-values
- https://en.wikipedia.org/wiki/Misuse_of_p-values. The p-value does not indicate the size or importance of the observed effect.
- Question: If we are fitting a multivariate regression and variable 1 ends with p-value .01 and variable 2 has p-value .001. How do we describe variable 2 is more significant than variable 1?
- Answer: you can say that variable 2 has a smaller p-value than variable 1. A p-value is a measure of the strength of evidence against the null hypothesis. It is the probability of observing a test statistic as extreme or more extreme than the one calculated from your data, assuming the null hypothesis is true. The smaller the p-value, the stronger the evidence against the null hypothesis and in favor of the alternative hypothesis. In your example, variable 2 has a smaller p-value than variable 1, which means that there is stronger evidence against the null hypothesis for variable 2 than for variable 1. However, it is important to note that a smaller p-value does not necessarily mean that one variable has a stronger effect or is more important than the other. Instead of comparing p-values directly, it would be more appropriate to look at effect sizes and confidence intervals to determine the relative importance of each variable.
- Effect Size: While a p-value tells you whether an effect exists, it does not convey the size of the effect. A p-value of 0.001 may be due to a larger effect size than one producing a p-value of 0.01, but this isn’t always the case. Effect size measures (like Cohen’s d for two means, Pearson’s r for two continuous variables, or Odds Ratio in logistic regression or contingency tables) are necessary to interpret the practical significance.
- Practical Significance: Even if both p-values are statistically significant, the practical or clinical significance of the findings should be considered. A very small effect size, even with a p-value of 0.001, may not be practically important.
- Question: do p-values show the relative importance of different predictors?
- P-values can indicate the statistical significance of a predictor in a model, but they do not directly measure the relative importance of different predictors.
- A p-value is a measure of the probability that the observed relationship between a predictor and the response variable occurred by chance under the null hypothesis. A smaller p-value suggests that it is less likely that the observed relationship occurred by chance, which often leads to the conclusion that the predictor is statistically significant.
- However, p-values do not tell us about the size or magnitude of an effect, nor do they directly compare the effects of different predictors. Two predictors might both be statistically significant, but one might have a much larger effect on the response variable than the other (There are several statistical measures that can be used to assess the relative importance of predictors in a model: Standardized Coefficients, Partial Correlation Coefficients, Variable Importance in Projection (VIP), Variable Importance Measures in Tree-Based Models, LASSO (Least Absolute Shrinkage and Selection Operator) and Relative Weights Analysis).
- Moreover, p-values are sensitive to sample size. With a large enough sample size, even tiny, unimportant differences can become statistically significant.
- Therefore, while p-values are a useful tool in model analysis, they should not be used alone to determine the relative importance of predictors. Other statistical measures and domain knowledge should also be considered.
- Why "Statistical Significance" Is Pointless. permutation p-value, bootstrap confidence interval.
Distribution of p values in medical abstracts
- http://www.ncbi.nlm.nih.gov/pubmed/26608725
- An R package with several million published p-values in tidy data sets by Jeff Leek.
nominal p-value and Empirical p-values
- Nominal p-values are based on asymptotic null distributions
- Empirical p-values are computed from simulations/permutations
- What is the concepts of nominal and actual significance level?
- The nominal significance level is the significance level a test is designed to achieve. This is very often 5% or 1%. Now in many situations the nominal significance level can't be achieved precisely. This can happen because the distribution is discrete and doesn't allow for a precise given rejection probability, and/or because the theory behind the test is asymptotic, i.e., the nominal level is only achieved for 𝑛→∞.
(nominal) alpha level
Conventional methodology for statistical testing is, in advance of undertaking the test, to set a NOMINAL ALPHA CRITERION LEVEL (often 0.05). The outcome is classified as showing STATISTICAL SIGNIFICANCE if the actual ALPHA (probability of the outcome under the null hypothesis) is no greater than this NOMINAL ALPHA CRITERION LEVEL.
- http://www.translationdirectory.com/glossaries/glossary033.htm
- http://courses.washington.edu/p209s07/lecturenotes/Week%205_Monday%20overheads.pdf
Normality assumption
Violating the normality assumption may be the lesser of two evils
Second-Generation p-Values
An Introduction to Second-Generation p-Values Blume et al, 2020
Small p-value due to very large sample size
- How to correct for small p-value due to very large sample size
- Too big to fail: large samples and the p-value problem, Lin 2013. Cited by ComBat paper.
- How to correct for small p-value due to very large sample size
- Does 𝑝-value change with sample size?
- The effect of sample on p-values. A simulation
- Power and Sample Size Analysis using Simulation
- Simulating p-values as a function of sample size
- Understanding p-values via simulations
- P-Values, Sample Size and Data Mining
Bayesian
- Bayesian believers, who adhere to Bayesian statistics, often have a different perspective on hypothesis testing compared to frequentist statisticians. In Bayesian statistics, the focus is on estimating the probability of a hypothesis being true given the data, rather than on the probability of the data given a specific hypothesis (as in p-values).
- Bayesian believers generally prefer using Bayesian methods, such as computing credible intervals or Bayes factors, which provide more directly interpretable results in terms of the probability of hypotheses. These methods can be seen as more informative than p-values, as they give a range of plausible values for the parameter of interest or directly compare the relative plausibility of different hypotheses.
T-statistic
See T-statistic.
ANOVA
See ANOVA.
Goodness of fit
Chi-square tests
Fitting distribution
- Fitting distributions with R
- Automated random variable distribution inference using Kullback-Leibler divergence and simulating best-fitting distribution
- MASS::fitdistr()
- Kullback-Leibler divergence for checking distribution adequacy
Normality distribution check
Anderson-Darling Test in R (Quick Normality Check)
Kolmogorov-Smirnov test
- Kolmogorov-Smirnov test
- An example of manual calculations and ks.test()
- ks_1sample.R: calculate the KS test statistic for the one-sample case
- ks_2sample.R: calculate the KS test statistic for two-sample distributions
- ks_3sample.R: calculate the permutation p-value and compare it with the p-value from ks.test()
- Lesson 22: Kolmogorov-Smirnov Goodness-of-Fit Test from stat.psu. Easy to understand the calculation.
- ks.test() in R
- Kolmogorov-Smirnov Test in R (With Examples)
- kolmogorov-smirnov plot
- Visualizing the Kolmogorov-Smirnov statistic in ggplot2
- On Misuses of the Kolmogorov–Smirnov Test for One-Sample Goodness-of-Fit 2024
Contingency Tables
How to Measure Contingency-Coefficient (Association Strength). gplots::balloonplot() and corrplot::corrplot() .
What statistical test should I do
What statistical test should I do?
Graphically show association
- Bar Graphs: Bar graphs can be used to compare the frequency of different categories in two variables. Each bar represents a category, and the height of the bar represents its frequency. You can create side-by-side bar graphs or stacked bar graphs to compare frequencies across categories. See Contingency Table: Definition, Examples & Interpreting (row totals) and Two Different Categorical Variables (column totals).
- Mosaic Plots: A mosaic plot gives a visual representation of the relationship between two categorical variables. It's a rectangular grid that represents the total population, and it's divided into smaller rectangles that represent the categories of each variable. The size of each rectangle is proportional to the frequency of each category. See Visualizing Association With Mosaic Plots.
- Categorical Scatterplots: In seaborn, a Python data visualization library, there are categorical scatterplots that adjust the positions of points on the categorical axis with a small amount of random "jitter" or using an algorithm that prevents them from overlapping. See Visualizing categorical data.
- Contingency Tables: While not a graphical method, contingency tables are often used in conjunction with graphical methods. A contingency table displays how many individuals fall in each combination of categories for two variables.
Q: How to guess whether two variables are associated by looking at the counts in a 2x2 contingency table:
- Observe the distribution of counts: If the counts are evenly distributed across the cells of the table, it suggests that there may not be a strong association between the two variables. However, if the counts are unevenly distributed, it suggests that there may be an association.
- Compare the diagonal cells: If the counts in the diagonal cells (top left to bottom right or top right to bottom left) are high compared to the off-diagonal cells, it suggests a positive association between the two variables. Conversely, if the counts in the off-diagonal cells are high, it suggests a negative association. See odds ratio >1 (pos association) or <1 (neg association).
- Calculate and compare the row and column totals: If the row and column totals are similar, it suggests that there may not be a strong association between the two variables. However, if the row and column totals are very different, it suggests that there may be an association.
Q: When creating a barplot of percentages from a contingency table, whether you calculate percentages by dividing counts by row totals or column totals? A: It depends on the question you’re trying to answer. See Contingency Table: Definition, Examples & Interpreting.
- Row Totals: If you’re interested in understanding the distribution of a variable within each row category, you would calculate percentages by dividing counts by row totals. This is often used when the row variable is the independent variable and you want to see how the column variable (dependent variable) is distributed within each level of the row variable.
- Column Totals: If you’re interested in understanding the distribution of a variable within each column category, you would calculate percentages by dividing counts by column totals. This is often used when the column variable is the independent variable and you want to see how the row variable (dependent variable) is distributed within each level of the column variable.
Barplot with colors for a 2nd variable.
Measure the association in a contingency table
- Phi coefficient: The Phi coefficient is a measure of association that is used for 2x2 contingency tables. It ranges from -1 to 1, with 0 indicating no association and values close to -1 or 1 indicating a strong association. The formula for Phi coefficient is: Phi = (ad - bc) / sqrt((a+b)(c+d)(a+c)(b+d)), where a, b, c, and d are the frequency counts in the four cells of the contingency table.
- Cramer's V: Cramer's V is a measure of association that is used for contingency tables of any size. It ranges from 0 to 1, with 0 indicating no association and values close to 1 indicating a strong association. The formula for Cramer's V is: V = sqrt(Chi-Square / (n*(min(r,c)-1))), where Chi-Square is the Chi-Square statistic, n is the total sample size, and r and c are the number of rows and columns in the contingency table.
- Odds ratio: The odds ratio is a measure of association that is commonly used in medical research and epidemiology. It compares the odds of an event occurring in one group compared to another group. The odds ratio can be calculated as: OR = (a/b) / (c/d), where a, b, c, and d are the frequency counts in the four cells of the contingency table. An odds ratio of 1 indicates no association, while values greater than 1 indicate a positive association and values less than 1 indicate a negative association.
Odds ratio and Risk ratio
- Odds ratio and Risk ratio/relative risk.
- In practice the odds ratio is commonly used for case-control studies, as the relative risk cannot be estimated.
- Relative risk is used in the statistical analysis of the data of ecological, cohort, medical and intervention studies, to estimate the strength of the association between exposures (treatments or risk factors) and outcomes.
- Odds Ratio Interpretation Quick Guide
- The odds ratio is often used to evaluate the strength of the association between two binary variables and to compare the risk of an event occurring between two groups.
- An odds ratio greater than 1 indicates that the event is more likely to occur in the first group, while an odds ratio less than 1 indicates that the event is more likely to occur in the second group.
- In general, a larger odds ratio indicates a stronger association between the two variables, while a smaller odds ratio indicates a weaker association.
- The ratio of the odds of an event occurring in one group to the odds of it occurring in another group
Treatment | Control ------------------------------------------------- Event occurs | A | B ------------------------------------------------- Event does not occur | C | D ------------------------------------------------- Odds | A/C | B/D ------------------------------------------------- Risk | A/(A+C) | B/(B+D)
- Odds Ratio = (A / C) / (B / D) = (AD) / (BC)
- Risk Ratio = (A / (A+C)) / (C / (B+D))
- Real example. In a study published in the Journal of the American Medical Association, researchers investigated the association between the use of nonsteroidal anti-inflammatory drugs (NSAIDs) and the risk of developing gastrointestinal bleeding. Suppose odds ratio = 2.5 and risk ratio is 1.5. The interpretation of the results in this study is as follows:
- The odds ratio of 2.5 indicates that the odds of gastrointestinal bleeding are 2.5 times higher in the group of patients taking NSAIDs compared to the group of patients not taking NSAIDs.
- The risk ratio of 1.5 indicates that the risk of gastrointestinal bleeding is 1.5 times higher in the group of patients taking NSAIDs compared to the group of patients not taking NSAIDs.
- In this example, both the odds ratio and the risk ratio indicate a significant association between NSAID use and the risk of gastrointestinal bleeding. However, the risk ratio is lower than the odds ratio, indicating that the overall prevalence of gastrointestinal bleeding in the study population is relatively low.
- What is the main difference in the interpretation of odds ratio and risk ratio?
- Odds are a measure of the probability of an event occurring, expressed as the ratio of the number of ways the event can occur to the number of ways it cannot occur. For example, if the probability of an event occurring is 0.5 (or 50%), the odds of the event occurring would be 1:1 (or 1 to 1).
- Risk is a measure of the probability of an event occurring, expressed as the ratio of the number of events that occur to the total number of events. For example, if 10 out of 100 people experience an event, the risk of the event occurring would be 10%.
- The main difference between the two measures is that the odds ratio is more sensitive to changes in the frequency of the event, while the risk ratio is more sensitive to changes in the overall prevalence of the event.
- This means that the odds ratio is more useful for comparing the odds of an event occurring between two groups when the event is relatively rare, while the risk ratio is more useful for comparing the risk of an event occurring between two groups when the event is more common.
Hypergeometric, One-tailed Fisher exact test
- ORA is inapplicable if there are few genes satisfying the significance threshold, or if almost all genes are DE. See also the flexible adjustment method for the handling of multiple testing correction.
- https://www.bioconductor.org/help/course-materials/2009/SeattleApr09/gsea/ (Are interesting features over-represented? or are selected genes more often in the GO category than expected by chance?)
- https://en.wikipedia.org/wiki/Hypergeometric_distribution. In a test for over-representation of successes in the sample, the hypergeometric p-value is calculated as the probability of randomly drawing k or more successes from the population in n total draws. In a test for under-representation, the p-value is the probability of randomly drawing k or fewer successes.
- http://stats.stackexchange.com/questions/62235/one-tailed-fishers-exact-test-and-the-hypergeometric-distribution
- Two sided hypergeometric test
- https://www.biostars.org/p/90662/ When computing the p-value (tail probability), consider to use 1 - Prob(observed -1) instead of 1 - Prob(observed) for discrete distribution.
- https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Hypergeometric.html p(x) = choose(m, x) choose(n, k-x) / choose(m+n, k).
drawn | not drawn |
-------------------------------------
white | x | | m
-------------------------------------
black | k-x | | n
-------------------------------------
| k | | m+n
For example, k=100, m=100, m+n=1000,
> 1 - phyper(10, 100, 10^3-100, 100, log.p=F) [1] 0.4160339 > a <- dhyper(0:10, 100, 10^3-100, 100) > cumsum(rev(a)) [1] 1.566158e-140 1.409558e-135 3.136408e-131 3.067025e-127 1.668004e-123 5.739613e-120 1.355765e-116 [8] 2.325536e-113 3.018276e-110 3.058586e-107 2.480543e-104 1.642534e-101 9.027724e-99 4.175767e-96 [15] 1.644702e-93 5.572070e-91 1.638079e-88 4.210963e-86 9.530281e-84 1.910424e-81 3.410345e-79 [22] 5.447786e-77 7.821658e-75 1.013356e-72 1.189000e-70 1.267638e-68 1.231736e-66 1.093852e-64 [29] 8.900857e-63 6.652193e-61 4.576232e-59 2.903632e-57 1.702481e-55 9.240350e-54 4.650130e-52 [36] 2.173043e-50 9.442985e-49 3.820823e-47 1.441257e-45 5.074077e-44 1.669028e-42 5.134399e-41 [43] 1.478542e-39 3.989016e-38 1.009089e-36 2.395206e-35 5.338260e-34 1.117816e-32 2.200410e-31 [50] 4.074043e-30 7.098105e-29 1.164233e-27 1.798390e-26 2.617103e-25 3.589044e-24 4.639451e-23 [57] 5.654244e-22 6.497925e-21 7.042397e-20 7.198582e-19 6.940175e-18 6.310859e-17 5.412268e-16 [64] 4.377256e-15 3.338067e-14 2.399811e-13 1.626091e-12 1.038184e-11 6.243346e-11 3.535115e-10 [71] 1.883810e-09 9.442711e-09 4.449741e-08 1.970041e-07 8.188671e-07 3.193112e-06 1.167109e-05 [78] 3.994913e-05 1.279299e-04 3.828641e-04 1.069633e-03 2.786293e-03 6.759071e-03 1.525017e-02 [85] 3.196401e-02 6.216690e-02 1.120899e-01 1.872547e-01 2.898395e-01 4.160339e-01 5.550192e-01 [92] 6.909666e-01 8.079129e-01 8.953150e-01 9.511926e-01 9.811343e-01 9.942110e-01 9.986807e-01 [99] 9.998018e-01 9.999853e-01 1.000000e+00 # Density plot plot(0:100, dhyper(0:100, 100, 10^3-100, 100), type='h')
Moreover,
1 - phyper(q=10, m, n, k)
= 1 - sum_{x=0}^{x=10} phyper(x, m, n, k)
= 1 - sum(a[1:11]) # R's index starts from 1.
Another example is the data from the functional annotation tool in DAVID.
| gene list | not gene list |
-------------------------------------------------------
pathway | 3 (q) | | 40 (m)
-------------------------------------------------------
not in pathway | 297 | | 29960 (n)
-------------------------------------------------------
| 300 (k) | | 30000
The one-tailed p-value from the hypergeometric test is calculated as 1 - phyper(3-1, 40, 29960, 300) = 0.0074.
Fisher's exact test
Following the above example from the DAVID website, the following R command calculates the Fisher exact test for independence in 2x2 contingency tables.
> fisher.test(matrix(c(3, 40, 297, 29960), nr=2)) # alternative = "two.sided" by default
Fisher's Exact Test for Count Data
data: matrix(c(3, 40, 297, 29960), nr = 2)
p-value = 0.008853
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.488738 23.966741
sample estimates:
odds ratio
7.564602
> fisher.test(matrix(c(3, 40, 297, 29960), nr=2), alternative="greater")
Fisher's Exact Test for Count Data
data: matrix(c(3, 40, 297, 29960), nr = 2)
p-value = 0.008853
alternative hypothesis: true odds ratio is greater than 1
95 percent confidence interval:
1.973 Inf
sample estimates:
odds ratio
7.564602
> fisher.test(matrix(c(3, 40, 297, 29960), nr=2), alternative="less")
Fisher's Exact Test for Count Data
data: matrix(c(3, 40, 297, 29960), nr = 2)
p-value = 0.9991
alternative hypothesis: true odds ratio is less than 1
95 percent confidence interval:
0.00000 20.90259
sample estimates:
odds ratio
7.564602
Fisher's exact test in R: independence test for a small sample
From the documentation of fisher.test
Usage:
fisher.test(x, y = NULL, workspace = 200000, hybrid = FALSE,
control = list(), or = 1, alternative = "two.sided",
conf.int = TRUE, conf.level = 0.95,
simulate.p.value = FALSE, B = 2000)
- For 2 by 2 cases, p-values are obtained directly using the (central or non-central) hypergeometric distribution.
- For 2 by 2 tables, the null of conditional independence is equivalent to the hypothesis that the odds ratio equals one.
- The alternative for a one-sided test is based on the odds ratio, so ‘alternative = "greater"’ is a test of the odds ratio being bigger than ‘or’.
- Two-sided tests are based on the probabilities of the tables, and take as ‘more extreme’ all tables with probabilities less than or equal to that of the observed table, the p-value being the sum of such probabilities.
Boschloo's test
https://en.wikipedia.org/wiki/Boschloo%27s_test
IID assumption
Ignoring the IID assumption isn’t a great idea
Chi-square independence test
- https://en.wikipedia.org/wiki/Chi-squared_test.
- Chi-Square = Σ[(O - E)^2 / E]
- We can see expected_{ij} = n_{i.}*n_{.j}/n_{..}
- The Chi-Square test statistic follows a Chi-Square distribution with degrees of freedom equal to (r-1) x (c-1)
- The Chi-Square test is generally a two-sided test, meaning that it tests for a significant difference between the observed and expected frequencies in both directions (i.e., either a greater than or less than difference).
- Chi-square test of independence by hand
> chisq.test(matrix(c(14,0,4,10), nr=2), correct=FALSE) Pearson's Chi-squared test data: matrix(c(14, 0, 4, 10), nr = 2) X-squared = 15.556, df = 1, p-value = 8.012e-05 # How about the case if expected=0 for some elements? > chisq.test(matrix(c(14,0,4,0), nr=2), correct=FALSE) Pearson's Chi-squared test data: matrix(c(14, 0, 4, 0), nr = 2) X-squared = NaN, df = 1, p-value = NA Warning message: In chisq.test(matrix(c(14, 0, 4, 0), nr = 2), correct = FALSE) : Chi-squared approximation may be incorrect
Exploring the underlying theory of the chi-square test through simulation - part 2
The result of Fisher exact test and chi-square test can be quite different.
# https://myweb.uiowa.edu/pbreheny/7210/f15/notes/9-24.pdf#page=4 R> Job <- matrix(c(16,48,67,21,0,19,53,88), nr=2, byrow=T) R> dimnames(Job) <- list(A=letters[1:2],B=letters[1:4]) R> fisher.test(Job) Fisher's Exact Test for Count Data data: Job p-value < 2.2e-16 alternative hypothesis: two.sided R> chisq.test(c(16,48,67,21), c(0,19,53,88)) Pearson's Chi-squared test data: c(16, 48, 67, 21) and c(0, 19, 53, 88) X-squared = 12, df = 9, p-value = 0.2133 Warning message: In chisq.test(c(16, 48, 67, 21), c(0, 19, 53, 88)) : Chi-squared approximation may be incorrect
Cochran-Armitage test for trend (2xk)
- Cochran–Armitage test for trend
- CochranArmitageTest(). CochranArmitageTest(dose, alternative="one.sided") if dose is a 2xk or kx2 matrix.
- ?prop.trend.test. prop.trend.test(dose[2,] , colSums(dose))
PAsso: Partial Association between ordinal variables after adjustment
https://github.com/XiaoruiZhu/PAsso
Cochran-Mantel-Haenszel (CMH) & Association Tests for Ordinal Table
- Contingency Tables In R
- Association Tests for Ordinal Table
- 5.3.5 - Cochran-Mantel-Haenszel Test psu.edu
- https://en.wikipedia.org/wiki/Cochran%E2%80%93Mantel%E2%80%93Haenszel_statistics
GSEA
See GSEA.
McNemar’s test on paired nominal data
https://en.wikipedia.org/wiki/McNemar%27s_test
R
Contingency Tables In R. Two-Way Tables, Mosaic plots, Proportions of the Contingency Tables, Rows and Columns Totals, Statistical Tests, Three-Way Tables, Cochran-Mantel-Haenszel (CMH) Methods.
Relationship between two variables
Spearman vs Pearson correlation
Pearson benchmarks linear relationship, Spearman benchmarks monotonic relationship. https://stats.stackexchange.com/questions/8071/how-to-choose-between-pearson-and-spearman-correlation
Testing using Student's t-distribution cor.test() (T-distribution with n-1 d.f.). The normality assumption is used in test. For estimation, it affects the unbiased and efficiency. See Sensitivity to the data distribution.
x=(1:100); y=exp(x); cor(x,y, method='spearman') # 1 cor(x,y, method='pearson') # .25
How to know whether Pearson's or Spearman's correlation is better to use? & Spearman’s Correlation Explained. Spearman's 𝜌 is better than Pearson correlation since
- it doesn't assume linear relationship between variables
- it is resistant to outliers
- it handles ordinal data that are not interval-scaled
Spearman vs Wilcoxon
By this post
- Wilcoxon used to compare categorical versus non-normal continuous variable
- Spearman's rho used to compare two continuous (including ordinal) variables that one or both aren't normally distributed
Spearman vs Kendall correlation
- Kendall's tau coefficient (after the Greek letter τ), is a statistic used to measure the ordinal association between two measured quantities.
- Spearman’s rho and Kendall’s tau from Statistical Odds & Ends
- Kendall Tau or Spearman's rho?
- Kendall’s Rank Correlation in R-Correlation Test
- Kendall’s tau is also more robust (less sensitive) to ties and outliers than Spearman’s rho. However, if the data are continuous or nearly so, Spearman’s rho may be more appropriate.
- Kendall’s tau is preferred when dealing with small samples. Pearson vs Spearman vs Kendall.
- Interpretation of concordant and discordant pairs: Kendall’s tau quantifies the difference between the percentage of concordant and discordant pairs among all possible pairwise events, which can be a more direct interpretation in certain contexts
- Although Kendall’s tau has a higher computation complexity (O(n^2)) compared to Spearman’s rho (O(n logn)), it can still be preferred in certain scenarios.
Pearson/Spearman/Kendall correlations
- Calculate Pearson, Spearman and Kendall correlation coefficients by hand
- Pearson vs Spearman vs Kendall. Formula in one page.
- Chapter 22: Correlation Types and When to Use Them from uic.edu
Jonckheere-Terpstra test
- clinfun::jonckheere.test(x, group)
- The JT test is suitable if one variable is continuous and the other one is a variable with a natural ordering (e.g. independent groups such as drug dosages). If the other variable is like a continuous time variable, it would be better to use the Kendall test.
phi correlation for binary variables
https://en.wikipedia.org/wiki/Phi_coefficient. A Pearson correlation coefficient estimated for two binary variables will return the phi coefficient.
set.seed(1) data <- data.frame(x=sample(c(0,1), 100, replace = T), y= sample(c(0,1), 100, replace = T)) cor(data$x, data$y) # [1] -0.03887781 library(psych) psych::phi(table(data$x, data$y)) # [1] -0.04
The real meaning of spurious correlations
https://nsaunders.wordpress.com/2017/02/03/the-real-meaning-of-spurious-correlations/
library(ggplot2)
set.seed(123)
spurious_data <- data.frame(x = rnorm(500, 10, 1),
y = rnorm(500, 10, 1),
z = rnorm(500, 30, 3))
cor(spurious_data$x, spurious_data$y)
# [1] -0.05943856
spurious_data %>% ggplot(aes(x, y)) + geom_point(alpha = 0.3) +
theme_bw() + labs(title = "Plot of y versus x for 500 observations with N(10, 1)")
cor(spurious_data$x / spurious_data$z, spurious_data$y / spurious_data$z)
# [1] 0.4517972
spurious_data %>% ggplot(aes(x/z, y/z)) + geom_point(aes(color = z), alpha = 0.5) +
theme_bw() + geom_smooth(method = "lm") +
scale_color_gradientn(colours = c("red", "white", "blue")) +
labs(title = "Plot of y/z versus x/z for 500 observations with x,y N(10, 1); z N(30, 3)")
spurious_data$z <- rnorm(500, 30, 6)
cor(spurious_data$x / spurious_data$z, spurious_data$y / spurious_data$z)
# [1] 0.8424597
spurious_data %>% ggplot(aes(x/z, y/z)) + geom_point(aes(color = z), alpha = 0.5) +
theme_bw() + geom_smooth(method = "lm") +
scale_color_gradientn(colours = c("red", "white", "blue")) +
labs(title = "Plot of y/z versus x/z for 500 observations with x,y N(10, 1); z N(30, 6)")
A New Coefficient of Correlation
A New Coefficient of Correlation Chatterjee, 2020 Jasa
Case control study
- See an example from the odds ratio calculation in https://en.wikipedia.org/wiki/Odds_ratio where it shows odds ratio can be calculated but relative risk cannot in the case-control study (useful in a rare-disease case).
- https://www.statisticshowto.datasciencecentral.com/case-control-study/
- https://medical-dictionary.thefreedictionary.com/case-control+study
- https://en.wikipedia.org/wiki/Case%E2%80%93control_study Cf. randomized controlled trial, cohort study
- https://www.students4bestevidence.net/blog/2017/12/06/case-control-and-cohort-studies-overview/
- https://quizlet.com/16214330/case-control-study-flash-cards/
Confidence vs Credibility Intervals
http://freakonometrics.hypotheses.org/18117
T-distribution vs normal distribution
- Normal Distribution vs. t-Distribution: What’s the Difference?
- Test normal distribution
set.seed(1); shapiro.test(rnorm(5000) ) # Shapiro-Wilk normality test # data: rnorm(5000) # W = 0.99957, p-value = 0.3352. --> accept H0 set.seed(1234567); shapiro.test(rnorm(5000) ) # Shapiro-Wilk normality test # data: rnorm(5000) # W = 0.99934, p-value = 0.06508 --> accept H0, but close to .05
Power analysis/Sample Size determination
See Power.
Common covariance/correlation structures
See psu.edu. Assume covariance [math]\displaystyle{ \Sigma = (\sigma_{ij})_{p\times p} }[/math]
- Diagonal structure: [math]\displaystyle{ \sigma_{ij} = 0 }[/math] if [math]\displaystyle{ i \neq j }[/math].
- Compound symmetry: [math]\displaystyle{ \sigma_{ij} = \rho }[/math] if [math]\displaystyle{ i \neq j }[/math].
- First-order autoregressive AR(1) structure: [math]\displaystyle{ \sigma_{ij} = \rho^{|i - j|} }[/math].
rho <- .8 p <- 5 blockMat <- rho ^ abs(matrix(1:p, p, p, byrow=T) - matrix(1:p, p, p))
- Banded matrix: [math]\displaystyle{ \sigma_{ii}=1, \sigma_{i,i+1}=\sigma_{i+1,i} \neq 0, \sigma_{i,i+2}=\sigma_{i+2,i} \neq 0 }[/math] and [math]\displaystyle{ \sigma_{ij}=0 }[/math] for [math]\displaystyle{ |i-j| \ge 3 }[/math].
- Spatial Power
- Unstructured Covariance
- Toeplitz structure
To create blocks of correlation matrix, use the "%x%" operator. See kronecker().
covMat <- diag(n.blocks) %x% blockMat
Counter/Special Examples
- Myths About Linear and Monotonic Associations: Pearson’s r, Spearman’s ρ, and Kendall’s τ van den Heuvel 2022
Math myths
Suppose X is a normally-distributed random variable with zero mean. Let Y = X^2. Clearly X and Y are not independent: if you know X, you also know Y. And if you know Y, you know the absolute value of X.
The covariance of X and Y is
Cov(X,Y) = E(XY) - E(X)E(Y) = E(X^3) - 0*E(Y) = E(X^3)
= 0,
because the distribution of X is symmetric around zero. Thus the correlation r(X,Y) = Cov(X,Y)/Sqrt[Var(X)Var(Y)] = 0, and we have a situation where the variables are not independent, yet have (linear) correlation r(X,Y) = 0.
This example shows how a linear correlation coefficient does not encapsulate anything about the quadratic dependence of Y upon X.
Significant p value but no correlation
Post where p-value = 1.18e-06 but cor=0.067. p-value does not say anything about the size of r.
Anscombe quartet
Four datasets have almost same properties: same mean in X, same mean in Y, same variance in X, (almost) same variance in Y, same correlation in X and Y, same linear regression.
Time series
- Time Series in 5-Minutes
- Why time series forecasts prediction intervals aren't as good as we'd hope
Structural change
Structural Changes in Global Warming
AR(1) processes and random walks
Spurious correlations and random walks
Measurement Error model
- Errors-in-variables models/errors-in-variables models or measurement error models
- Simulation‐‐Selection‐‐Extrapolation: Estimation in High‐‐Dimensional Errors‐‐in‐‐Variables Models Nghiem 2019
Polya Urn Model
The Pólya Urn Model: A simple Simulation of “The Rich get Richer”
Dictionary
- Prognosis is the probability that an event or diagnosis will result in a particular outcome.
- For example, on the paper Developing and Validating Continuous Genomic Signatures in Randomized Clinical Trials for Predictive Medicine by Matsui 2012, the prognostic score .1 (0.9) represents a good (poor) prognosis.
- Prostate cancer has a much higher one-year overall survival rate than pancreatic cancer, and thus has a better prognosis. See Survival rate in wikipedia.
Statistical guidance
- Statistical guidance to authors at top-ranked scientific journals: A cross-disciplinary assessment
- How to get your article rejected by the BMJ: 12 common statistical issues Richard Riley
Books, learning material
- Anna’s Archive
- Methods in Biostatistics with R ($)
- Modern Statistics for Modern Biology (free)
- Principles of Applied Statistics, by David Cox & Christl Donnelly
- Statistics by David Freedman,Robert Pisani, Roger Purves
- Wiley Online Library -> Statistics (Access by NIH Library)
- Computer Age Statistical Inference: Algorithms, Evidence and Data Science by Efron and Hastie 2016
- UW Biostatistics Summer Courses (4 institutes)
- Statistics for Biology and Health Springer.
- Bayesian Essentials with R
- Core Statistics Simon Wood
Social
JSM
- 2019
- JSM 2019 and the post.
- An R Users Guide to JSM 2019
Following
- Jeff Leek, https://twitter.com/jtleek
- Revolutions, http://blog.revolutionanalytics.com/
- RStudio Blog, https://blog.rstudio.com/
- Sean Davis, https://twitter.com/seandavis12, https://github.com/seandavi
- Stephen Turner, https://twitter.com/genetics_blog
COPSS
考普斯會長獎 COPSS